Навигация
Достатня умова ергодичності
1.3 Достатня умова ергодичності
Теорема 1.3.1 (Теорема Фостера).
Регулярна Марковська ланцюг з безперервним часом і рахунковим числом станів ергодична
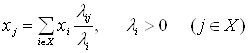
має нетривіальне рішення ![]() таке, що
таке, що ![]() При цьому існує єдиний стаціонарний розподіл, що збігається з ергодичним. [2, с. 8-14]
При цьому існує єдиний стаціонарний розподіл, що збігається з ергодичним. [2, с. 8-14]
Ергодичність досліджуємо відповідно до теореми 1.3.1. Розглянемо умови теореми.
Регулярність треба з того, що ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
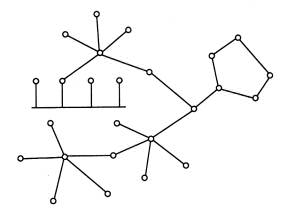
Відповідно до малюнка 1.1, одержимо:
![]() ,
, ![]() ,
, ![]() .
.
Таким чином, регулярність виконується.
Тому що всі стани повідомляються з нульовим, тобто в будь-який стан ![]() можна перейти з нульового
можна перейти з нульового ![]() й у
й у ![]() можна перейти з будь-якого стану, шляхом надходження, обслуговування й відходу заявок з мережі.
можна перейти з будь-якого стану, шляхом надходження, обслуговування й відходу заявок з мережі.
Примітка – тут ураховується, що матриця переходів ![]() неприводима.
неприводима.
Як нетривіальне рішення системи рівнянь із теореми 1.3.1 візьмемо ![]() . Тоді для ергодичності буде потрібно, щоб
. Тоді для ергодичності буде потрібно, щоб ![]() . Тоді одержимо,
. Тоді одержимо,
![]() ,
,
де
![]() ,
,

Останній ряд сходиться по ознаці порівняння, якщо сходиться ряд
|

Умова (1.3.1) і є шукана умова ергодичності. Якщо ця умова буде виконаються, то буде існувати єдиний стаціонарний розподіл, що збігається з ергодичним.
2. Полумарковська модель мережі із трьома вузлами
Нехай є відкрита мережа масового обслуговування, що складає із трьох вузлів, у яку надходить найпростіший потік заявок з параметром ![]() . Причому, у першу систему масового обслуговування, що входить заявка надходить із імовірністю
. Причому, у першу систему масового обслуговування, що входить заявка надходить із імовірністю ![]() . Часи обслуговування заявок в
. Часи обслуговування заявок в ![]() -ом вузлі задані функцією розподілу часу обслуговування
-ом вузлі задані функцією розподілу часу обслуговування ![]() -им приладом однієї заявки
-им приладом однієї заявки ![]() ,
, ![]() . При цьому накладає наступна вимога
. При цьому накладає наступна вимога
![]() ,
, ![]() . (2.1)
. (2.1)
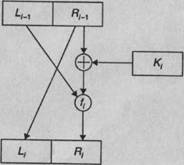
Дисципліни обслуговування заявок у системах мережі LCFS PR - заявка, що надходить в ![]() -ий вузол, витісняє заявку із приладу й починає обслуговуватися. Витиснута із приладу заявка стає в початок черги. Схематично мережа зображена на малюнку 2.1.
-ий вузол, витісняє заявку із приладу й починає обслуговуватися. Витиснута із приладу заявка стає в початок черги. Схематично мережа зображена на малюнку 2.1.
Стан мережі описується випадковим процесом
![]() ,
,
де ![]() ,
, ![]() ,
, ![]() - залишковий час обслуговування заявки, що коштує в
- залишковий час обслуговування заявки, що коштує в ![]() -ой позиції.
-ой позиції.
Примітка. Випадковий процес
![]() ,
,
де ![]() - число заявок в
- число заявок в ![]() -ом вузлі в момент
-ом вузлі в момент ![]()
![]() , не є марковським процесом. Для марковизації процесу включаємо додаткові змінні. Щоб
, не є марковським процесом. Для марковизації процесу включаємо додаткові змінні. Щоб ![]() був марковським процесом, додаткові змінні візьмемо, як залишкові часи від моменту часу
був марковським процесом, додаткові змінні візьмемо, як залишкові часи від моменту часу ![]() до повного завершення відповідних часів. Виходить, процес
до повного завершення відповідних часів. Виходить, процес ![]() - марковський процес.
- марковський процес.
Таким чином, з вищесказаного треба, що побудовано полумарковська модель відкритої мережі із трьома вузлами.
Похожие работы
... і, нарешті, крипторотоколу. Це все було зроблено для того, щоб полегшати формалізування опису протоколів для доказування їхньої стійкості. Розділ 3. Оцінка стійкості криптографічних протоколів на основі імовірнісних моделей 3.1. Методика оцінки стійкості Формальний доказ стійкості в рамках обчислювальної моделі складається з трьох етапів. 1. Формальна поведінка учасників протоколу і ...
... видів риб та водоплавних та навколоводних птахів. З птахів домінують гусеподібні, сивкоподібні, а також зустрічаються норцеподібні, лелекоподібні, журавлеподібні і горобцеподібні. Розділ 4. Проектування екологічних мереж Ратнівського району 4.1 Загальні поняття Сучасна стратегія охорони природи полягає у забезпеченні динамічної екологічної рівноваги окремих регіонів, пошуку різноманітних ...
... Так працюють протоколи ТСР/IP. Вони забезпечують передачу інформації між двома комп'ютерами, а всі інші протоколи з їх допомогою реалізують різноманітні послуги Iнтернета. 4.5 Електронна пошта Комп’ютерні мережі в залежності від призначення можуть надавати користувачам різні послуги. Найбільш розповсюдженими видами послуг є: електронна пошта; телеконференції; передача файлів; віддалене ...
... інованим) порядком. При використанні детермінованих методів колізії неможливі, але вони є більш складними в реалізації і збільшують вартість мережного обладнання. 3.1 Метод доступу до каналів комп’ютерних мереж з перевіркою несучої та виявленням колізій CSMA/CD Метод багатостанційного доступу до середовища з контролем несучої та виявленням колізій (Carrier Sense Multiply Access / Collision ...

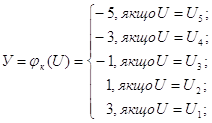
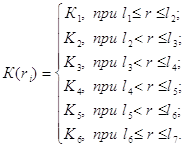

0 комментариев