Обтекание трамплинной горы потоком воздуха

4. Обтекание трамплинной горы потоком воздуха

4.1. Концептуальная постановка задачи

Эта глава посвящена задаче обтекания воздухом трамплинной горы. Цель данной работы - спрогнозировать поле скоростей ветра вблизи трамплина, чтобы можно было использовать эти данные в модели полета лыжника и более точно оценить влияние ветра на полет.

Сам трамплин достаточно узок и не играет значительной роли в формировании воздухных потоков, поэтому рассматривается только гора.

Для решения задачи была привлечена теория пограничного слоя. Воздух в пограничном слое вблизи земли считается вязкой несжимаемой жидкостью. Это не противоречит очевидной сжимаемости воздуха: как будет показано ниже, условие сжимаемости (согласно [8], где используется термин "искусственная сжимаемость") будет выглядеть точно так же, как и условие несжимаемости. Рассматривается двумерная постановка задачи течения жидкости в достаточно большой области, чтобы течение во входном и выходном сечениях и на верхней границе можно было считать строго горизонтальным. Нам известны экспериментальные данные по среднесезонным и среднегодовым скоростям ветра на разных высотах, их можно использовать для проверки и выбора входных данных. В [9], например, скорости ветра заданы в виде нечетких чисел, у которых функция принадлежности имеет вероятностный смысл, а носитель измеряется в м/с:

Скорости ветра в среднем по зимнему сезону (среднее значение):

скорость ветра на высоте от 40 до 120 м (4.9 м/с):

("0 до 2"/0.188 , "2 до 5"/0.420 , "5 до 10"/0.352 , "10 до 15"/ 0.037, "свыше 15"/0.003)

скорость ветра на высоте 500 м (11.4 м/с):

("0 до 2"/0.061 , "2 до 5"/0.125 , "5 до 10"/0.336 , "10 до 15"/ 0.241, "свыше 15"/0.237)

скорость ветра на высоте от 1000 м (11.3 м/с):

("0 до 2"/0.073 , "2 до 5"/0.114 , "5 до 10"/0.290 , "10 до 15"/ 0.280, "свыше 15"/0.243)

скорость ветра на высоте от 1500 м (11.6 м/с):

("0 до 2"/0.087 , "2 до 5"/0.076 , "5 до 10"/0.276 , "10 до 15"/ 0.306, "свыше 15"/0.255)

Среднегодовые скорости ветра (среднее значение):

скорость ветра на высоте от 40 до 120 м (4.7 м/с):

("0 до 2"/0.214 , "2 до 5"/0.442 , "5 до 10"/0.316 , "10 до 15"/ 0.026, "свыше 15"/0.002)

скорость ветра на высоте 500 м (8.9 м/с):

("0 до 2"/0.117 , "2 до 5"/0.194 , "5 до 10"/0.370 , "10 до 15"/ 0.187, "свыше 15"/0.132)

скорость ветра на высоте 1000 м (9.2 м/с):

("0 до 2"/0.110 , "2 до 5"/0.183 , "5 до 10"/0.336 , "10 до 15"/ 0.225, "свыше 15"/0.146)

скорость ветра на высоте 1500 м (9.4 м/с):

("0 до 2"/0.126 , "2 до 5"/0.168 , "5 до 10"/0.284 , "10 до 15"/ 0.274, "свыше 15"/0.148)

Как видно из этих данных, начиная с высоты 500 метров скорость ветра мало изменяется, значит, эту величину можно принять в качестве толщины пограничного слоя. Рассматриваемая область имеет прямоугольную форму с выпуклостью на нижней границе - трамплинной горой.

Контрольный счет проводился при следующих граничных условиях:

во входном сечении: (16)

в выходном сечении: (17)

на верхней границе: (18)

на нижней границе: (19)

Рассматриваются достаточно малые скорости, так как при сильном ветре прыжки запрещены. Малость скоростей позволяет пренебречь конвективными членами и считать течение ламинарным. Силой тяжести на данном этапе мы также пренебрегаем. Надо сказать, что мы сознаем некоторую натянутость такой постановки, в следующей работе эта задача будет решена уже с учетом и конвективного члена, и силы тяжести.

4.2. Математическая постановка

Течение вязкой несжимаемой жидкости описывается следующей системой уравнений [7]:

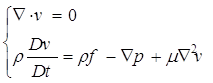(20)

Для двумерной постановки эти уравнения приводятся к следующему виду:

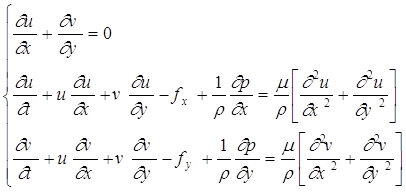(21)

Согласно [8] для описания сжимаемых жидкостей первое уравнение из (21) может быть заменено на следующее: 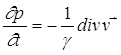, однако так как в данной работе рассматривается стационарное течение, то производная по времени равна нулю, и это соотношение приобретает вид, идентичный условию несжимаемости.

Задача решалась с граничными условиями (16)-(19).

В качестве области брался прямоугольник с выступом в виде трамплинной горы. Сам трамплин достаточно узок, и не вносит существенного вклада в формирование воздушного потока, поэтому он не рассматривается. Трамплинная гора состоит из участка необработанного склона - дуги окружности с известным радиусом кривизны, длиной и высотой, участка обработанного склона, предназначенного для приземления лыжников - прямой с известным углом к горизонтали и длиной и закругления с известным радиусом для безопасности тех, кто улетает за пределы допустимой дальности.

Похожие работы

Задача о движении снаряда

Скачать

11197

1

9

... . Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений. Целью данной курсовой работы является моделирование движения снаряда. модель параметр движение снаряд Постановка задачи   Снаряд пущен с Земли с начальной скоростью v0 под углом  к ее поверхности; требуется найти траекторию его движения (y), расстояние S между ...