Золотой пятиугольник; построение Евклида

5.3. Золотой пятиугольник; построение Евклида.

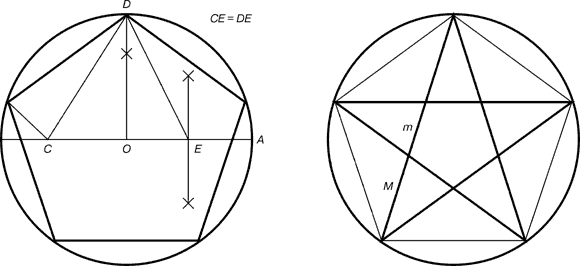
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).

	Рис.6. Построение правильного пятиугольника и пентаграммы.

Для построения пентаграммы необходимо построить правильный пятиугольник.

Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».

стр.75)

Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника

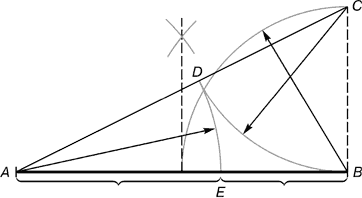
из центра описанной окружности. Начнем с

отрезка АВЕ, разделенного в среднем и

крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.

Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС - 3a - 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,

180=(3a -180) + (3a-180) + (180 - a)

Откуда 5a=360, значит a=72.

Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.

Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:

CN² = а² – (а/2j) ²= а² (1-4j ²)

Отсюда имеем (АС/а) ² = (1+1/2j) ² + (1-1/4j ²) = 2+1/j = 1 + j =j ²

Итак, АС = jа = jАВ = АЕ, что и требовалось доказать

5.4.Спираль Архимеда.

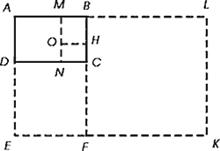
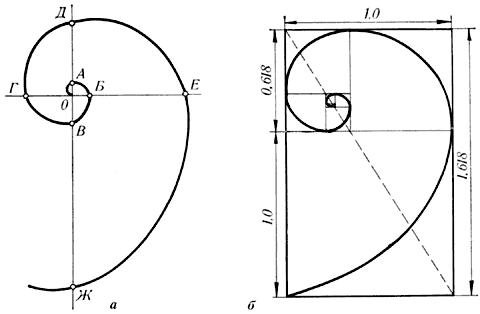
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.

В настоящее время спираль Архимеда широко используется в технике.  

6.Числа Фибоначчи.

С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи)

В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке" . "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.

Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.

Рассмотрим одну такую задачу:

"Сколько пар кроликов в один год от одной пары рождается?

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения"

Месяцы	1	2	3	4	5	6	7	8	9	10	11	12
Пары кроликов	2	3	5	8	13	21	34	55	89	144	233	377

Табл.1 Ряд Фибоначчи при u1=1

 

Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:

u₁, u₂ … u_n

в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2

u_n=u_n-1+u_n-2.

Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то превосходящая, то не достигающая его.

Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:

1:1 = 1.0000, что меньше фи на 0.6180

2:1 = 2.0000, что больше фи на 0.3820

3:2 = 1.5000, что меньше фи на 0.1180

5:3 = 1.6667, что больше фи на 0.0486

8:5 = 1.6000, что меньше фи на 0.0180

По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.

Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.

Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1 : 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.

При делении каждого числа на следующее за ним через одно, получаем число 0.382

1:0.382=2.618

Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.

Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.

Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам - выпуклым и звездчатым.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16...(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2..., во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?

Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5... Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).

Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.

В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения x^S+1 – x^S – 1 = 0.

Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.

Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.

7.Золотое сечение в искусстве.

7.1. Золотое сечение в живописи.

Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..

Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.

В картине Рафаэля "Избиение младенцев" просматривается другой элемент золотой пропорции - золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.

Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие .

7.2. Пирамиды золотого сечения.

Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух - прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича

8. Заключение.

Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.

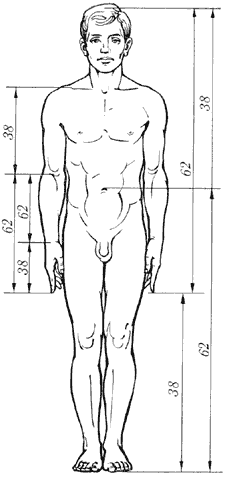
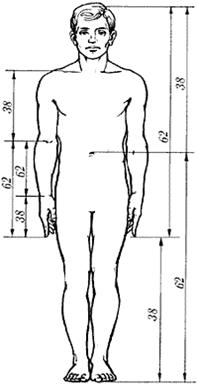
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.

Раковина наутилуса закручена подобно золотой спирали.

Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.

Возбуждение струны в точке , делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.

На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.

Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».

Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»

Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.

Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: "Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении"

Список литературы

1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.

2. Журнал "Наука и техника"

3. Журнал «Квант», 1973, № 8.

4. Журнал «Математика в школе», 1994, № 2; № 3.

5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.

6. Стахов А. Коды золотой пропорции.

7.Воробьев Н.Н. "Числа Фибоначчи" - М.: Наука 1964

8. "Математика - Энциклопедия для детей" М.: Аванта +, 1998

9. Информация из интернета.