Навигация
Вспомогательные числа и вспомогательные сравнения
1.5 Вспомогательные числа и вспомогательные сравнения
Пусть {1, 2, …, ri, …, mi, ..., li, …, K – 1} – приведенная система наименьших, натуральных вычетов по модулю K. Тогда, очевидно, существуют такие числа r1, r2, r3, m1, m2, m3 и l1, l2 и l3, принадлежащие этой системе, что
r1Z – X º 0 mod K или r1Z º X mod K, (1.50)
Z – r2Y º 0 mod K или r2Y º Z mod K, (1.51)
r3X + Y º 0 mod K или r3X º –Y mod K, (1.52)
Z – m1X º 0 mod K, (1.53)
m2Z – Y º 0 mod K, (1.54)
X + m3Y º 0 mod K, (1.55)
Z 2 – l1XY º 0 mod K, (1.56)
Y 2 + l2ZX º 0 mod K, (1.57)
X 2 + l3ZY º 0 mod K. (1.58)
Умножая сравнения (1.50)–(1.52), получим
r1r2r3ZXYº – ZXY mod K,
отсюда
r1r2r3 º –1 mod K. (1.59)
Cложим сравнение (1.50) и (1.51) и, учитывая (1.26), получим
r1Z – X + Z – r2Y º r1Z + (Z – X) – r2Y º r1Z + Y – r2Y º
º r1Z – Y(r2 – 1) º 0 mod K,
а учитывая, что Z º r2Y mod K (cм. (1.51)), получим
r1r2Y – Y(r2 – 1) º 0 mod K,
отсюда
r1r2 – r2 + 1 º 0 mod K Þ r1r2 º r2 – 1 mod K. (1.60)
Умножая сравнение (1.60) на r3 и учитывая (1.59), получим
r2r3 – r3 + 1 º 0 mod K Þ r2r3 º r3 – 1 mod K. (1.61)
Умножая (1.61) на r1 и учитывая (1.59), получим
r1r3 – r1 + 1 º 0 mod K Þ r1r3 º r1 – 1 mod K. (1.62)
Из сравнений (1.50) и (1.53) получим
r1m1 º1 mod K, (1.63)
а из сравнений (1.51), (1.54) и (1.52),(1.55) получим соответственно
r2m2 º 1 mod K, (1.64)
r3m3 º 1mod K. (1.65)
Сложим сравнения (1.50) и (1.55) и, учитывая (1.51) и (1.60), получим
r1Z – X + X + m3Y º r1r2Y + m3Y º Y (r2 – 1 + m3) º 0 mod K Þ
Þ m3 º 1 – r2 mod K. (1.66)
Cложим сравнения (1.52) и (1.54) и, учитывая (1.50) и (1.62), получим
m2Z – Y + r3X + Yº m2Z + r3r1Z º Z(m2 + r3r1) ºº Z(m2 +r1 – 1) º 0 mod K, Þ m2 º 1 – r1 mod K. (1.67)
Из сравнения (1.51) вычтем сравнение (1.53) и, учитывая (1.52) и (1.61), получим
Z – r2Y – Z + m1X º m1X – r2(–r3X) º X(m1 + r2r3) º
º X(m1 + r3 – 1) º 0 mod K Þ m1 º 1 – r3 mod K. (1.68)
Решая совместно сравнения (1.56) и (1.50) и принимая во внимание сравнение (1.51), получим
Z 2 – l1XY º Z 2 – l1r1ZY º Z(Z – l1r1Y) º Z(r2Y – l1r1Y) º
º ZY(r2 – l1r1) º 0 mod K Þ l1r1 º r2 mod K. (1.69)
Решая совместно сравнения (1.57) и (1.51) и принимая во внимание (1.52), получим
Y 2 + l2ZX º Y 2 + l2r2YX º Y(Y + l2r2X) º Y(–r3X + l2r2X) º XY(l2r2 – r3) º 0 mod K Þ l2r2 º r3 mod K. (1.70)
Решая совместно сравнения (1.58) и (1.52) и принимая во внимание (1.50), получим
X 2 + l3ZY º X2 + l3Z(–r3X) º X(X – l3r3Z) º X(r1Z – l3r3Z) º ZX(r1 – l3r3) º 0 mod K, Þ l3r3 º r1 mod K. (1.71)
Из сравнения (1.69) вычтем сравнение (1.63) и, принимая во внимание (1.60), получим
l1r1 – m1r1 º r2 – 1 º r1r2 mod K,
отсюда, сокращая на r1, получим l1 – m1 º r2 mod K, а с учетом (1.68) имеем
l1 º r2 + m1 º r2 + 1 – r3 mod K,
отсюда, так как l1, r2 и r3 меньше K, получим
l1 = r2 – r3 + 1. (1.72)
Из сравнения (1.70) вычтем сравнение (1.64) и, принимая во внимание (1.61), получим
l2r2 – m2r2 º r3 – 1 º r2r3 mod K,
отсюда, сокращая на r2, получим l2 – m2 º r3 mod K, а с учетом (1.67) имеем
l2 º r3 + m2 º r3 + 1 – r1 mod K,
отсюда, так как l2, r3 и r1 меньше K, получим
l2 = r3 – r1 + 1. (1.73)
Из сравнения (1.71) вычтем сравнение (1.65) и, принимая во внимание (1.62), получим
l3r3 – m3r3 º r1 – 1 º r1r3 mod K,
отсюда, сокращая на r3, получим l3 – m3 º r1 mod K, а с учетом (1.66) имеем
l3 º r1 + m3 º r1 + 1 – r2 mod K,
отсюда, так как l3, r1 и r2 меньше K, имеем
l3 = r1 – r2 + 1. (1.74)
1.5.6. Проведем анализ равенств, полученных в п. 1.5.5.
Из равенства (1.72) следует, что
а) r2 ³ r3,
тогда сложим равенства (1.73) и (1.74):
l2 +l3 = r3 – r1 + 1 + r1 – r2 + 1 = r3 – r2 + 2,
отсюда, так как числа l2 и l3 натуральные, следует, что
б) r3 ³ r2.
отношения а) и б) возможны только при условии, что
r2 = r3. (1.75)
Из равенства (1.73) следует, что
в) r3 ³ r1,
тогда сложим равенства (1.72) и (1.74):
l1 + l3 = r2 – r3 + 1 + r1 – r2 + 1 = r1 – r3 + 2,
отсюда, так как числа l1 и l3 натуральные, следует, что
г) r1 ³ r3,
отношения в) и г) возможны только при условии, что
r1 = r3. (1.76)
Благодаря равенствам (1.75) и (1.76) имеем равенство чисел r1, r2 и r3, тогда
r1 = r2 = r3 = r. (1.77)
Из равенств (1.72)–(1.74) с учетом равенств (1.77) следует, что
l1 = 1, l2 = 1 и l3 = 1. (1.78)
Благодаря (1.77) сравнения (1.60)–(1.62) примут вид
r2 – r + 1 º 0 mod K, (1.79)
а сравнение (1.59) будет выглядеть следующим образом:
r3 º –1 mod K. (1.80)
Благодаря (1.78) сравнения (1.56)–(1.58) примут вид
Z 2 – XY º 0 mod K,
Y 2 + ZX º 0 mod K,
X 2 + ZY º 0 mod K,
а с учетом (1.26) –
(X + Y)2 – XYº 0 mod K, (1.81)
(Z – X)2 + ZXº 0 mod K, (1.82)
(Z – Y)2 + ZYº 0 mod K. (1.83)
Похожие работы
... Декарт в первую очередь идеолог: он основатель философской школы, он формирует понятия, совершенствует систему буквенных обозначений, но в его творческом наследии мало новых конкретных приемов. В противоположность ему Пьер Ферма мало пишет, но по любому поводу может придумать массу остроумных математических трюков (см. там же “Теорема Ферма”, ”Принцип Ферма”, ”Метод бесконечного спуска Ферма”). ...
... живем в 4х-мерном пространстве-времени, да еще с неевклидовой метрикой” – это будет пустое словоблудие. Интересную связь можно обнаружить между 3-мерностью бытия и двумя теоремами: теоремой Ферма и теоремой Пифагора. Великая теорема Ферма, по имеющимся сообщениям в печати, наконец-то доказана. Однако можно предложить иной взгляд на эту теорему. Если присмотреться к уравнению известной теоремы ...
... и крупных компаний. Соответствующим образом делится и программное обеспечение (ПО) в этом секторе рынка. Системы автоматизации деятельности средних и крупных компаний имеют не только модули для работы с финансовой информацией, но и программы автоматизации делопроизводства, управления проектами, распределения товаров по складам и др. Среди наиболее распространенных и активно продвигаемых систем ...
... данных по сети. ЗАКЛЮЧЕНИЕ В рамках данного дипломного проектирования перед студентом Малышевым А.А. была поставлена задача: на основе алгоритма RSA для шифрования блоков данных, построить алгоритм и реализовать программный продукт для шифрования потоков данных. В результате выполнения дипломного проектирования был составлен принципиальный алгоритм для решения поставленной задачи. Далее он был ...
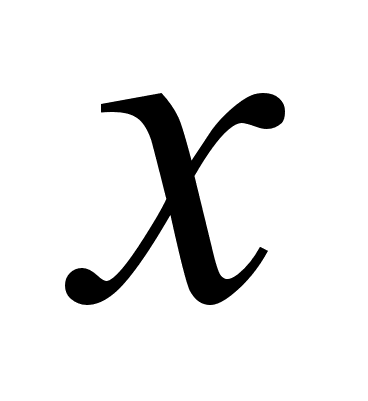
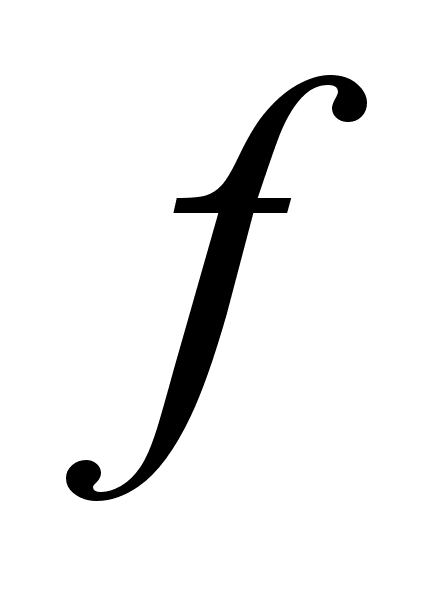
0 комментариев