Навигация
Этап – определение начального опорного плана
2 этап – определение начального опорного плана.
В полученном случае начальный опорный план будут составлять искусственные переменные, входящие в ограничения с коэффициентами +1 :{ y5 ; y6 }. Новых искусственных переменных для данной задачи вводить не требуется.
3 этап – заполнение исходной симплекс-таблицы.
Исходная симплекс-таблица для нашей двойственной задачи будет иметь вид:
![]() В столбец "текущий базис" ставим переменные, начального опорного плана : { y5 ; y6 }.
В столбец "текущий базис" ставим переменные, начального опорного плана : { y5 ; y6 }.
В столбец "сi" ставим их коэффициенты в целевой функции.
В столбец "А0" ставим вектор ограничений Е : а10 = 1 ;а20 = 1 .
В самую верхнюю строку таблицы ставим коэффициенты cj при соответствующих переменных в целевой функции:c1 = 1 ; c2 = 1 ; c3 = 1 ; c4 = 1 ; c5 = 0 ; c6 = 0 .
В столбцы "А1", ...., "А6" ставим соответствующие коэффициенты матрицы ограничений А.
Вычисляем оценки по формулам
D0 = ![]() ; .Dj =
; .Dj = ![]() – cj
– cj
и ставим их в самую нижнюю строку симплекс-таблицы (строку оценок) :
D0 = ![]() = 0 * 1 + 0 * 1 = 0D1 =
= 0 * 1 + 0 * 1 = 0D1 = ![]() – c1 = 0 * 4 + 0 * 3 – 1 = – 1
– c1 = 0 * 4 + 0 * 3 – 1 = – 1
D2 = ![]() – c2 = 0 * 3 + 0 * 7 – 1 = – 1D3 =
– c2 = 0 * 3 + 0 * 7 – 1 = – 1D3 = ![]() – c3 = 0 * 8 + 0 * 1 – 1 = – 1
– c3 = 0 * 8 + 0 * 1 – 1 = – 1
D4 = ![]() – c4 = 0 * 2 + 0 * 3 – 1 = – 1D5 =
– c4 = 0 * 2 + 0 * 3 – 1 = – 1D5 = ![]() – c5 = 0 * 1 + 0 * 0 – 0 = 0
– c5 = 0 * 1 + 0 * 0 – 0 = 0
D6 = ![]() – c6 = 0 * 0 + 0 * 1 – 0 = 0
– c6 = 0 * 0 + 0 * 1 – 0 = 0
4 этап – пересчет симплекс-таблицы.
1. Если j ³ 0 для всех j = 1, 2, .... , n , то данный план (в столбце "текущий базис") – оптимален. В нашем случае это условие не выполняется, значит, текущий базис можно улучшить.
2. Если имеются k < 0 и в столбце Аk все элементы aik ![]() 0 , то целевая функция не ограничена сверху на допустимом множестве и данная задача не имеет смысла. В нашем случае видим, что целевая функция сверху ограничена.
0 , то целевая функция не ограничена сверху на допустимом множестве и данная задача не имеет смысла. В нашем случае видим, что целевая функция сверху ограничена.
3. Если имеются j < 0 и в столбцах Аj , соответствующих этим оценкам, существует хотя бы один элемент aik > 0, то возможен переход к новому лучшему плану, связанному с большим значением целевой функции. У нас так и есть.
4. Переменная хk, которую необходимо ввести в базис, для улучшения плана соответствует наименьшей отрицательной оценке j. Столбец Ak, содержащий эту оценку называется ведущим. В нашем случае все оценки одинаковы. Поэтому в качестве ведущего столбца выберем любую оценку, например, третью: k = 3.
5. Ищем min{ ai0 / ai1 } = min{ 1/8 ; 1/1 } = 1/8– этот минимум достигается при i = 1. Значит, r = 1первая строка – ведущая. (на рисунке помечена стрелкой)
Ведущий элементark = a13 = 8 (на рисунке выделен)
6. Заполняем новую симплекс-таблицу.
В столбец "текущий базис" вместо переменной у5 ставим переменную у3 .
В столбец "сi" ставим коэффициент переменной у3 в целевой функции.
Самая верхняя строка таблицы всегда остаётся неизменной.
Пересчитываем ведущую строку по формуле ![]() :
:
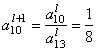
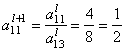
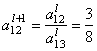
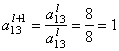
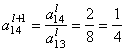
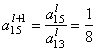
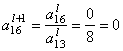
После этого пересчитываем остальные строки по формуле
![]() :
:
вторая строка (i = 2)
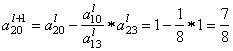
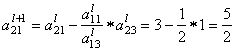
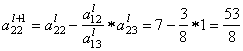
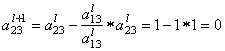
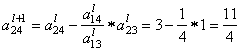
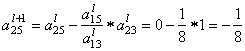
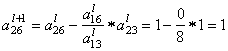
Пересчитываем и заполняем строку оценок:
D0 = ![]() = 1 *
= 1 * ![]() + 0 *
+ 0 * ![]() =
= ![]() D1 =
D1 = ![]() – c1 = 1 *
– c1 = 1 * ![]() + 0 *
+ 0 * ![]() – 1 = –
– 1 = – ![]()
D2 = ![]() – c2 = 1 *
– c2 = 1 * ![]() + 0 *
+ 0 * ![]() – 1 = –
– 1 = – ![]() D3 =
D3 = ![]() – c3 = 1 * 1 + 0 * 0 – 1 = 0
– c3 = 1 * 1 + 0 * 0 – 1 = 0
D4 = ![]() – c4 = 1 *
– c4 = 1 * ![]() + 0 *
+ 0 * ![]() – 1 = –
– 1 = – ![]()
D5 = ![]() – c5 = 1 *
– c5 = 1 * ![]() + 0 *
+ 0 * ![]() – 0 =
– 0 = ![]() D6 =
D6 = ![]() – c6 = 1 * 0 + 0 * 1 – 0 = 0
– c6 = 1 * 0 + 0 * 1 – 0 = 0
После этого повторяем 4 этап до тех пор, пока не будет выполнен п.1 (все j ³ 0).
В нашем случае имеются j < 0 и наименьшая среди них 4 . Значит ведущим столбцом на данном шаге будет A4 (пометим его стрелкой).
Ищем min{ ai0 / ai4 } = min{![]() :
:![]() ;
; ![]() :
:![]() } = min{
} = min{![]() ;
; ![]() } =
} = ![]() – этот минимум достигается при i = 2. Значит, r = 2вторая строка – ведущая (на рисунке помечена стрелкой).
– этот минимум достигается при i = 2. Значит, r = 2вторая строка – ведущая (на рисунке помечена стрелкой).
Таким образом, в новый текущий базис вместо переменной у6 надо ввести переменную у4 .
Пересчитываем все элементы новой симплекс-таблицы.
Пересчитываем ведущую строку (вторую):
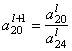 =
= ![]() :
:![]() =
= ![]()
![]() =
= ![]()
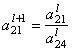 =
= ![]() :
:![]() =
= ![]()
![]() =
= ![]()
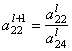 =
= ![]() :
:![]() =
= ![]()
![]() =
= ![]()
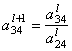 = 0 :
= 0 :![]() = 0
= 0
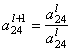 =
= ![]() :
:![]() = 1
= 1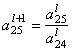 = –
= – ![]() :
:![]() = –
= – ![]()
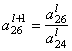 = 1 :
= 1 : ![]() =
= ![]()
Приведенные выше и ниже вычисления представлены в весьма подробном виде. Это сделано из тех соображений, что как опять таки показывает практика, даже не смотря на достаточно хорошее понимание и усвоение теоретического материала, ошибки зачастую возникают именно при выполнении элементарных арифметических операций. Не следует думать, что средняя школа осталась позади, и вы всё можете посчитать в уме. Поэтому всем студентам мы советуем не лениться и подробно расписывать все арифметические действия (особенно с дробями).#
Пересчитываем оставшуюся строку (первую):
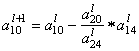 =
= ![]() –
– ![]()
![]() =
= ![]() –
– ![]() =
= ![]() =
= ![]()
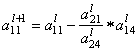 =
= ![]() –
– ![]()
![]() =
= ![]() –
– ![]() =
= ![]() =
= ![]()
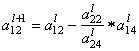 =
= ![]() –
– ![]()
![]() =
= ![]() –
– ![]() = –
= – ![]() = –
= – ![]()
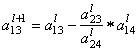 = 1 – 0
= 1 – 0 ![]() = 1
= 1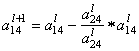 =
= ![]() –
– ![]() = 0
= 0
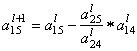 =
= ![]() –
– ![]()
![]() =
= ![]() +
+ ![]() =
= ![]() =
= ![]()
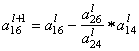 = 0 –
= 0 – ![]()
![]() = –
= – ![]()
Пересчитываем и заполняем строку оценок:
D0 = ![]() = 1 *
= 1 * ![]() + 1 *
+ 1 * ![]() =
= ![]() =
= ![]()
D1 = ![]() – c1 = 1 *
– c1 = 1 * ![]() + 1 *
+ 1 * ![]() – 1 =
– 1 = ![]() –
– ![]() =
= ![]()
D2 = ![]() – c2 = 1 *
– c2 = 1 * ![]() + 1 *
+ 1 * ![]() – 1 =
– 1 = ![]() –
– ![]() =
= ![]() =
= ![]()
D3 = ![]() – c3 = 1 * 1 + 1 * 0 – 1 = 0
– c3 = 1 * 1 + 1 * 0 – 1 = 0
D4 = ![]() – c4 = 1 * 0 + 1 * 1 – 1 = 0
– c4 = 1 * 0 + 1 * 1 – 1 = 0
D5 = ![]() – c5 = 1 *
– c5 = 1 * ![]() + 1 *
+ 1 * ![]() – 0 =
– 0 = ![]() =
= ![]()
D6 = ![]() – c6 = 1
– c6 = 1 ![]() + 1
+ 1 ![]() – 0 =
– 0 = ![]()
Повторяем 4-й этап. При проверке п. 1 видим, что все j ³ 0 . Следовательно, данный план {у3, у4} (в столбце "текущий базис") – оптимален. Больше пересчитывать симплекс-таблицу не нужно.
Решение задачи линейного программирования полностью содержится в последней симплекс-таблице.
Значения переменных находятся в столбце А0 возле соответствующих переменных. В нашем случае, мы видим, что у3 = ![]() , у4 =
, у4 = ![]() . Переменные у1 и у2 не входят в базис, поэтому их значения будут равны нулю. Таким образом, вектор переменных будет выглядеть так: Y =
. Переменные у1 и у2 не входят в базис, поэтому их значения будут равны нулю. Таким образом, вектор переменных будет выглядеть так: Y = ![]() .
.
Значение целевой функции – это значение оценки 0 . В нашем случае g = 0 = ![]() .
.
Значения двойственных переменных находятся в строке оценок возле искусственных переменных. В нашем случае это 5 и 6 , то есть х1 = ![]() , х2 =
, х2 = ![]() . Таким образом, вектор двойственных переменных будет выглядеть так:Х =
. Таким образом, вектор двойственных переменных будет выглядеть так:Х = ![]() .
.
Итак, мы получили решение прямой задачи (которая у нас была двойственной): Y = ![]()
и двойственной задачи к данной (которая у нас была прямой):
Х = ![]()
Значения целевых функций при этом будут совпадать:f = g = ![]() .
.
Найдем цену игры:n = ![]() =
= ![]()
Далее найдем коэффициенты смешанной стратегии
для первого игрока по формуле рi = ![]() :
:
Р = ![]() =
= ![]() ,
,
для второго игрока по формуле qi = ![]() :
:
Q = ![]() =
= ![]() .
.
Особо "продвинутые" студенты при нахождении решения задачи линейного программирования, чтобы не считать симплекс-метод вручную академическим способом, могут воспользоваться средствами MS Excel. Это гораздо быстрее и удобнее.#
Ответ: смешанная стратегия для первого игрока Р = ![]() ,
,
смешанная стратегия для второго игрока Q = ![]() ,
,
цена игры n = ![]() .
.
Симплекс-методом можно найти решение матричной игры произвольной размерности. Графическим же способом найти решение можно лишь для игры размерности 2 х n.
В ответе мы должны получить смешанные стратегии – два вектора PA = (p1, p2) и QB = (q1, q2, …, qn). Причем, p2 = 1 – p1.
В этом случае выигрыш игрока А, соответствующий j-той чистой стратегии игрока В, будет вычисляться по формуле:
aj* = a1j p1 + a2j p2 = a1j p1 + a2j (1 – p1) = (a1j – a2j) p1 + a2j
Нахождение наименьшего гарантированного выигрыша для игрока А подразумевает минимизацию данного выражения.
По условию наша игра имеет размерность 2 х n. То есть j = ![]() . В итоге будем иметь n аналогичных выражений, которые надо минимизировать. После этого согласно принципу максимина из найденных минимумов нужно выбрать наибольший:
. В итоге будем иметь n аналогичных выражений, которые надо минимизировать. После этого согласно принципу максимина из найденных минимумов нужно выбрать наибольший:
a = ![]()
Решим графическим способом предыдущий числовой пример.
![]()
В данном случае будем иметь четыре уравнения, соответствующие четырем возможным чистым стратегиям игрока В:a1* = р1 + 3
a2* = –4р1 + 7
a3* = 7р1 + 1
a4* = –р1 + 3
Чтобы определить наилучший результат из наихудших, построим нижнюю огибающую четырех заданных прямых (на рисунке выделена жирной линией). Эта огибающая представляет минимальный гарантированный выигрыш игрока А, независимо от того, что делает игрок В. Точка максимума нижней огибающей – это и есть решение задачи по принципу максимина. Координатами этой точки будут р1 – одна из вероятностей смешанной стратегии игрока А и a – выигрыш игрока А.
# Заметим, что содержательной является только часть графика, заключенная в интервале 0 ≤ р1 ≤ 1 . Все линии и точки, лежащие за пределами этого интервала не принимаются во внимание. #
"На глаз" координаты точки максимума нижней огибающей видны плохо. Точка максимума нижней огибающей – это точка пересечения прямой 3 и прямой 4. Найдем её точные координаты, решив систему соответствующих уравнений:
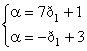 Þ
Þ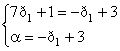 Þ
Þ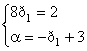 Þ
Þ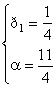
Далее находим p2: p2 = 1 – p1 = 1 – ![]() =
= ![]()
Итак, для игрока А все ясно:
смешанная стратегия игрока А: Р = ![]() ,
,
выигрыш игрока А:a = ![]() .
.
Аналогичные рассуждения нужно повторить и для игрока В.
Точка максимума нижней огибающей – это точка пересечения прямой 3 и прямой 4. Значит оптимальная смешанная стратегия игрока В определяется двумя стратегиями В3 и В4 соответственно.
Проигрыш игрока В, соответствующий i-той чистой стратегии игрока A, будет вычисляться по формуле:
вi* = ai3 q3 + ai4 q4 = ai3 q3 + ai4 (1 – q3) = (ai3 – ai4) q3 + ai4
В данном случае будем иметь два уравнения, соответствующие двум возможным чистым стратегиям игрока А:
в1* = 6q3 + 2
в2* = –2q3 + 3
Решив систему этих двух уравнений, найдем q3 – одну из вероятностей смешанной стратегии игрока В и в – выигрыш игрока В:
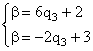 Þ
Þ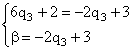 Þ
Þ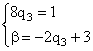 Þ
Þ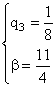
Далее находим q4: q4 = 1 – q3 = 1 – ![]() =
= ![]()
Все выяснили также и для игрока В:
смешанная стратегия игрока В: Q = ![]()
проигрыш игрока В:в = ![]()
Выигрыш игрока А и проигрыш игрока В совпадают – это и будет ценой игры.
Ответ: смешанная стратегия для первого игрока Р = ![]() ,
,
смешанная стратегия для второго игрока Q = ![]() ,
,
цена игры n = ![]() .
.
Видим, что ответы в случае решения задачи симплекс-методом и в случае решения этой же задачи графическим методом совпали.
Мораль вышесказанного такова, что если имеем задачу размерности 2 х n и под рукой нет компьютера, то точное решение можно получить с помощью графического метода.
Если имеем задачу размерности m х 2 , то делаем то же самое, поменяв игроков местами и транспонировав платежную матрицу. #
Если же под рукой есть компьютер, то такие задачи удобнее решать симплекс-методом средствами MS Excel. Если же поставленная задача любой большей размерности, то решить ее можно только симплекс-методом либо вручную, либо опять таки средствами MS Excel.
Раздел 5. Принятие решения в условиях нескольких критериев выбора 5.1 Постановка задачи, основные понятия
Все перечисленные классические критерии выбора не охватывают всевозможные практические ситуации. К каждой конкретной практической ситуации ЛПР может выработать свой "новый" критерий, который будет более точно количественно и качественно описывать данную ситуацию.
К сожалению или счастью, жизнь устроена несколько сложнее и достаточно часто бывает невозможно описать ситуацию одним критерием. Даже в обыденной жизни мы практически никогда не используем единственный критерий, например, при выборе подарка ко дню рождения, или при выборе блюд из меню в кафе, или при выборе места, куда поехать в отпуск.
А представьте, что вы – проектировщик баз данных. В таком случае при выборе оптимального проекта баз данных вам следует учитывать тоже несколько критериев: объем занимаемой оперативной памяти, средняя скорость одной операции, размер программного кода, аппаратные требования, обучаемость обслуживающего персонала, возможность и стоимость сопровождения и прочие. Ниже будут рассматриваться прикладные задачи с уже изученными нами критериями: Байеса, Лапласа и др. Но если вы все-таки – например, проектировщик баз данных, то вам надо будет вместо них рассматривать "свои" критерии, которые являются спецификой вашего рода деятельности.
Такие ситуации описываются многокритериальными задачами принятия решений.
Теоретически можно представить себе случай, когда в допустимом множестве альтернатив существует одна альтернатива, которая лучше всех по всем критериям сразу. Очевидно, что она и будет лучшей.
Однако на практике такое бывает не всегда. Для решения таких задач разработаны специальные методы. Надо сказать, что данное научное направление сравнительно ново – оно развивается последние 30 – 40 лет. Уже известные методы корректируются, обобщаются, разрабатываются новые. Приятно отметить, что одним из основоположников и всемирно признанным гуру данного научного направления является наш почти соотечественник В.В. Подиновский.
Рассмотрим приведенный выше числовой пример. И применим к нему все изученные нами критерии. Результаты отобразим в таблице:
Заметим, что стратегия (альтернатива) А4 по всем девяти критериям хуже, чем любая другая стратегия. Её можно убрать из рассмотрения, при этом результат выбора не изменится. Это утверждает принцип Парето. Оставшиеся альтернативы А1, А2, А3, будут образовывать множество Парето для данной задачи.
Из допустимого множества альтернатив множество Парето образуют те альтернативы, каждая из которых не хуже по всем критериям, чем любая альтернатива, не вошедшая во множество Парето, а хотя бы по одному критерию – лучше.
Согласно принципу Парето оптимальная альтернатива содержится во множестве Парето. Если, например исходная задача содержит 100 альтернативных решений, а множество Парето состоит из 20 альтернатив, то применение принципа Парето в 5 раз уменьшает размерность задачи, соответственно в 5 раз увеличится скорость работы программы, реализующей решение такой задачи!
Далее полученную многокритериальную задачу принятия решения на множестве Парето можно свести к однокритериальной, введя некий обобщенный критерий Z* как функцию от предыдущих частных критериев. Обобщенный критерий Z* в литературе еще называют функцией полезности. Процесс сведения многокритериальной задачи к однокритериальной называется свёрткой.
5.2 Линейные свёрткиНачнем с линейных свёрток. Все линейные свёртки основываются на принципе: "низкая оценка по одному критерию может быть компенсирована высокой оценкой по другому".
Рассмотрим простую линейную аддитивную свёртку:
Z* = max![]() ,
,
![]()
То есть, данная свёртка подсчитывает, сколько раз та или иная стратегия была оптимальной. Результаты отобразим в таблице:
В последнем столбе таблицы размещены результаты свёртки. Как видим, оптимальной стратегией является А3.
Такая свёртка является самой простой из линейных, она не учитывает количественных показателей значений критериев.
Рассмотрим линейную аддитивную свёртку с нормирующими множителями:
Z* = max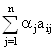 ,
,
где aj = ![]() – нормирующие множители.
– нормирующие множители.
Как видим, оптимальной стратегией также является А3. Но в этом случае уже нет такого количественного отрыва как в предыдущей простой линейной свёртке. Да и стратегия А2 уже не кажется очень сильно плохой. Если бы были чуть другие начальные данные, то ответы двух рассмотренных вариантов свёрток могли бы и не совпасть.
Линейная аддитивная свёртка с нормирующими множителями позволяет работать с количественными критериями, имеющими, как в нашем случае, разные единицы измерений.
Рассмотрим линейную аддитивную свёртку с весовыми коэффициентами:
Z* = max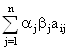 ,
,
где aj – те же нормирующие множители,
вj – весовые коэффициенты, отражающие относительный
вклад частных критериев в общий критерий.
Весовые коэффициенты принято указывать уже нормированными величинами (Sвj = 1).
Очевидно, что в каждой отдельной конкретной ситуации частные критерии по-разному влияют на общий суперкритерий. Поэтому естественно им придать в общей формуле разный удельный вес. Это можно сделать с помощью весовых коэффициентов. Но где же их взять? Обычно ЛПР сам назначает каждому критерию весовые коэффициенты на свой "мудрый" взгляд. На этом этапе строгая математическая наука заканчивается – конечный результат лежит целиком на совести ЛПР и зависит от его опыта и интуиции в данной сфере. Однако от такого субъективизма никуда не денешься – нельзя же всю жизнь формализовать с помощью математических формул!
Как видим, при неизменном условии задачи оптимальной получилась стратегия А2, хотя в двух предыдущих свёртках она "пасла задних". Все дело в весовых коэффициентах!
5.3 Максиминная и лексикографическая свёртки
Максиминная свёртка – это самый простой способ построения обобщенного критерия (суперкритерия), основанный на применении уже хорошо нам известного принципа максимина.
Пусть мы имеем оценки некоторых объектов (альтернатив) по n критериям. Каждый из критериев имеет свою размерность, и эти размерности обычно не совпадают. Поэтому для начала нужно нормировать все имеющиеся оценки. Делается это с помощью нормирующих множителей – на основе исходной матрицы оценок строится новая матрица с такими элементами:
cij = ![]()
где aj = ![]() – нормирующие множители.
– нормирующие множители.
Далее к полученной матрице применяем принцип максимина. Посмотрим, как это делается на нашем примере:
Исходную матрицу мы, так же как и ранее, дополнили справа еще одним столбцом, в который внесли значения минимальных элементов каждой пересчитанной строки.
Из элементов добавленного столбца выбираем наибольший. Строка, в которой он стоит и будет оптимальной альтернативой. В данном случае оптимальной будет альтернатива А1.
Недостаток максиминной свёртки – это то, что она учитывает только те критерии, которые дают самые плохие оценки, все остальные критерии игнорируются. Из-за этого максиминную свёртку используют не слишком часто, чаще используют линейные и мультипликативные свёртки. Зато такой подход всегда дает гарантированный результат, ниже которого исхода не будет.
А что делать, если максиминная свёртка даст несколько одинаковых результатов (такое тоже бывает!), а ЛПР необходимо выбрать одно решение? Для такого интересного случая А. Джоффрион предложил использовать так называемую лексикографическую свёртку. Делается это так. Берутся две (или несколько) оптимальные альтернативы, полученные методом максиминной свёртки, и из них выбирается наилучшая методом линейной свёртки.
Как видим, с такими числовыми данными максиминная свёртка оптимальными считает альтернативы А1 и А2 . Теперь после максиминной свёртки применим к альтернативам А1 и А2 линейную свёртку:
В результате получили однозначный ответ: оптимальной является альтернатива А1 .
5.4 Мультипликативные свёрткиРассмотрим мультипликативную свёртку с нормирующими множителями:
Z* = max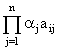 ,
,
где aj – нормирующие множители.
Мультипликативная свёртка основывается на постулате: "низкая оценка хотя бы по одному критерию влечет за собой низкое значение функции полезности". Действительно, если вы выбираете торт, и он – несвежий, то это обстоятельство никак не может быть компенсировано его красотой или ценой.
Оптимальной стратегией снова является А3.
Посмотрим, какие результаты даст мультипликативная свёртка с весовыми коэффициентами:
Z* = max ,
,
где aj – нормирующие множители,
вj – весовые коэффициенты.
Итоги отражены в таблице:
Оптимальной стратегией снова является А3.
В конце еще раз напомним непременное правило: перед тем, как применять какую-либо свёртку нужно автоматически всегда выделять множество Парето. И именно для множества Парето применять свёртки. Иначе вы или ваша программа будете выполнять лишнюю ненужную работу.
5.5 Многокритериальный выбор на языке бинарных отношенийДо этого были рассмотрены случаи, когда все критерии оценивали все альтернативы. Все альтернативы можно было сравнить друг с другом по каждому критерию. А что делать, если не все альтернативы будут оценены всеми критериями? В таком случае появятся альтернативы, не сравнимые между собой по некоторым критериям. Рассмотрим такой случай на нашем примере (уберем из него некоторые оценки):
При таком условии альтернативы можно сравнить между собой лишь попарно. Такие попарные сравнения называются бинарными отношениями. Обозначается бинарное отношение (на примере критерия Байеса из нашей таблицы) А1RА2 – альтернатива А1 лучше альтернативы А2.
Дадим математически точное определение бинарных отношений.
Бинарным отношением на множестве Ω называется произвольное подмножество R множества Ω Х Ω , где Ω Х Ω – это множество всех упорядоченных пар (ai ;aj) , где ai , aj Î Ω . #
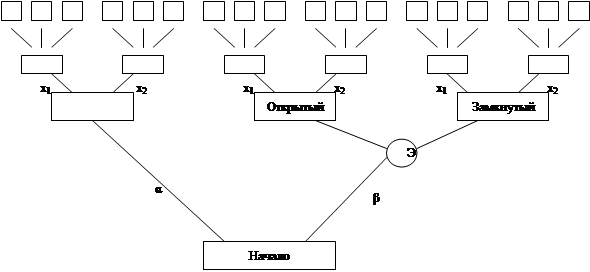
Бинарные отношения очень удобно изображать наглядно. Представим четыре стратегии из нашего примера в виде точек на плоскости. Если имеем, что какая-то альтернатива лучше другой, то проведем стрелку от лучшей альтернативы к худшей. На примере критерия Байеса из нашей таблицы имеем А1RА2 , поэтому на плоскости проведем стрелку от точки А1 к точке А2. Аналогичным образом поступим со всеми начальными данными из таблицы. Заметим, что бинарные отношения не исключают отношения элемента с самим собой. На рисунке такое бинарное отношение будет задаваться петлёй со стрелкой. В результате получим следующую картину:
Подобные фигуры называются ориентированными графами. Точки – это вершины графа, стрелки между точками – это дуги графа.
Дадим математически точное определение графа.
Графом называется пара (Е, е), где Е – непустое конечное множество элементов (вершин), е – конечное (возможно и пустое) множество пар элементов из Е (множество дуг). #
Две вершины, соединенные дугой, называются смежными вершинами. Дуга, соединяющая две вершины, называется инцидентной этим вершинам. Две вершины, соединенные дугой, называются инцидентными этой дуге.
Как же произвести выбор наилучшего элемента из имеющихся альтернатив (наилучшей вершины графа)? Для этого сначала необходимо определить, что же будет являться наилучшей вершины (наилучшими вершинами) графа. На этот счет имеются две исторически сложившиеся в теории графов точки зрения.
1)Максимальным элементом множества Ω по бинарному отношению R называется такой элемент х Î Ω , что "у Î Ω выполняется отношение хRy .
Иначе говоря, максимальный элемент множества должен быть "лучше" каждого элемента этого множества. Не исключается и то, что он может быть "лучше" самого себя, кроме этого максимальный элемент может быть одновременно и "хуже" какого-либо элемента этого множества. Слова "лучше" и "хуже" не совсем верно передают смысл бинарных отношений.
Для графов понятие максимальный элемент – это вершина, из которой исходят стрелки во все остальные вершины графа. Например, на рис. 1 максимальным элементом будет вершина А1 – из неё выходят стрелки во все остальные вершины графа.
2)Оптимальным по Парето элементом множества Ω по бинарному отношению R называется такой элемент х Î Ω , что ù$у Î Ω для которого выполнялось бы отношение уRх .
Иначе говоря, оптимальный по Парето элемент множества – это такой элемент, "лучше" которого в рассматриваемом множестве нет.
Для графов понятие оптимальный по Парето элемент – это вершина, в которую не входит ни одна стрелка. Например, на рис. 1 оптимальным по Парето элементом будет вершина А1 – в неё не входит ни одна стрелка.
Видим, что два разных подхода к определению наилучшего элемента в нашем примере дали одинаковый результат. Но такое бывает не всегда.
Рассмотрим несколько примеров.
У графа на рис. 2 максимальным элементом будет вершина А1 – из неё выходят стрелки во все остальные вершины графа. Оптимальных по Парето элементов у данного графа нет.
У графа на рис. 3 максимальным элементом будет также вершина А1 – из неё выходят стрелки во все остальные вершины графа. Заметим: то, что в неё входит стрелка из вершины А4 , по определению совершенно не важно. Оптимальных по Парето элементов у данного графа нет.
У графа на рис. 4 максимальными элементами будут вершины А1 и А4 – из них выходят стрелки во все остальные вершины графа. Оптимальных по Парето элементов у данного графа нет.
У графа на рис. 5 максимального элемента нет. Оптимальными по Парето элементами будут вершины А1 и А4 – в них не входит ни одна стрелка.
Отметим очевидные особенности.
У графа либо нет максимальных элементов, либо есть.
Оптимальными по Парето элементами могут быть несколько вершин графа, либо таковых может не быть.
В графе не может один (или одни) элемент быть максимальным, а другой (или другие) элемент быть оптимальным по Парето.
Итак, если имеется задача многокритериального выбора, описанная на языке бинарных отношений, то её удобно представить наглядно в виде графа. Однако такое удобство хорошо для небольшого количества вершин (альтернатив). Если вершин довольно много, то вся наглядность пропадает и легко можно запутаться. В таком случае граф удобно представить в виде матрицы смежности или матрицы инцидентности.
Матрица смежности вершин графа – это квадратная матрица размера m x m (m – это количество вершин) с элементами:
сij = ![]()
По матрицам смежности искать максимальные элементы и элементы, оптимальные по Парето – одно удовольствие! Максимальные элементы – это те, чьи строки состоят из всех единиц (кроме себя самих – там может быть как нуль, так и единица). А оптимальные по Парето элементы – это те, чьи столбцы состоят из всех нулей.
Матрица инцидентности графа – это матрица, строки которой соответствуют вершинам, а столбцы – дугам. При этом предполагается, что граф не должен иметь петель.
Элементы матрицы инцидентности будут такими:
сij = 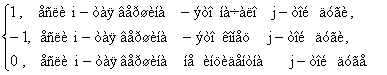
Видим, что каждый столбец должен содержать одну единицу и одну минус единицу, остальные элементы столбцов – нули. То есть каждая дуга из одной вершины выходит и в другую вершину входит.
Налицо также очевидна закономерность: максимальные элементы – это те, чьи строки содержат единиц на одну меньше, чем количество строк (вершин), а оптимальные по Парето элементы – это те, чьи строки не содержат минус единиц.
Используя замечательные особенности матриц смежности и инцидентности графов, не составит большого труда разрабатывать компьютерные программы по принятию решений для задач выбора, описанных на языке бинарных отношений.
Раздел 6. Принятие корпоративных решений 6.1 Групповая оценка объектов
В приведенном выше материале подразумевалось, что ЛПР – это некий эксперт-аналитик, принимающий решение по поставленной проблеме. А если проблемой занимаются несколько экспертов? А решение то должно быть одно! Такая задача называется задачей группового выбора или задачей принятия корпоративного решения.
Тут нужно отметить один важный психологический момент. Взрослого человека (начиная лет с 5-10) практически никогда невозможно заставить изменить свое мнение. (Есть, конечно, "безотказные" методы типа насилия, или денежного подкупа, но они к науке не имеют никакого отношения.) Поэтому эксперты в группе всегда будут:
- иметь разные мнения по поводу набора критериев, по которым надо оценивать альтернативные решения;
- иметь разные мнения о сравнительной значимости (весовых коэффициентах) критериев;
- давать разные оценки альтернатив по критериям;
- кроме этого эксперты будут иметь разную компетентность.
Исходя из таких очевидных фактов, можно с уверенностью утверждать, что у группы экспертов всегда должен быть руководитель.
Каждый из экспертов группы в принятии своего решения будет руководствоваться своим опытом и своими знаниями. Будем надеяться, что вышеприведенный материал окажет экспертам некую посильную помощь. Материал данного подраздела предназначен для руководителей групп экспертов, которые на основе всех решений группы обязаны приять единственное правильное решение.
Вспомним, как обычно преодолеваются групповые разногласия? В подавляющем большинстве случаев это делается с помощью обыкновенного голосования.
Рассмотрим формализованный пример голосования. В таблице начальных данных отражены количественные оценки четырёх альтернативных решений девятью экспертами:
Для начала необходимо найти множество Парето: это будут альтернативы А1, А2, А4. Оптимальное решение будем искать среди них. Для проведения голосования определим функцию полезности:
Z* = max![]() ,
,
![]()
В последнем столбе таблицы размещены результаты голосования. Как видим, оптимальным решением является альтернатива А4 – за неё проголосовало пять экспертов из девяти – больше половины.
При всей простоте, широкой распространенности и многовековой исторической традиции использования метод голосования имеет один существенный недостаток. Голосование не считается с мнением меньшинства. Мнение меньшинства полностью игнорируется! Но иногда ведь случается, (правда очень редко) что именно среди этого меньшинства и находилось наилучшее решение! Кроме практического результата голосование наносит психологический удар по тем экспертам, мнения которых были отброшены. Математические методы принятия корпоративных решений стараются исправить этот недостаток. Учитываются мнения всех экспертов.
Рассмотрим такую функцию полезности с нормирующими множителями:
Z* = max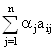 ,
,
где aj = ![]() .
.
В этом случае оптимальным решением является альтернатива А1.
Заметим, что такой способ учитывает также и то, что эксперты пользовались разными шкалами оценок объектов.
А теперь попробуем учесть ещё и степень компетентности каждого эксперта. Функция полезности при этом будет выглядеть так:
Z* = max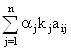 ,
,
где aj – те же нормирующие множители,
kj – коэффициенты компетентности экспертов.
Ниже будет рассмотрен один из способов определения коэффициентов компетентности экспертов.
А пока рассмотрим ту же задачу с уже якобы вычисленными коэффициентами компетентности экспертов. В таблице снова сначала – условие, ниже – результаты:
А теперь мы получили в качестве оптимальной альтернативу А2.
Надо отметить, что приведенные два последних способа принятия группового решения годятся только для согласованных суждений экспертов. Согласованность – это степень расхождения мнений экспертов. Методика вычисления согласованности оценок экспертов достаточно сложна. По необходимости с ней можно ознакомиться в специальной литературе по принятию корпоративных решений.
Если эксперты честно оценивают реальный объект, то их оценки не должны сильно расходиться. Если же они все-таки существенно расходятся, то можно получить часто упоминаемую в литературе так называемую "среднюю температуру по больнице". Действительно, если сложить температуру всех высокотемпературных больных и температуру тел в морге, а потом поделить на общее количество замеров, то можно получить 36,6°. Свидетельствует ли это о том, что "в среднем" все находящиеся в больнице здоровы?
Если согласованность оказалась низкой, то нужно пытаться выяснить причину расхождений и по возможности попытаться устранить её. Часто причиной может быть отсутствие важной информации у некоторых экспертов. В некоторых случаях эксперты разбиваются на две устойчивые группы. Группы нужно уметь выявлять и обрабатывать отдельно.
6.2 Определение коэффициентов компетентности экспертовТеперь опишем одну из методик определения коэффициентов компетентности экспертов.
Рассмотрим опять нашу задачу, в которой принимали участие девять экспертов. Предложим каждому из девяти экспертов в отдельности самому сформировать экспертную группу. Каждый эксперт может включить в экспертную группу произвольное количество участников. Себя он может как включать в эту группу, так и нет. В результате получим матрицу Х, состоящую из элементов хij :
Х = {хij} = ![]()
Допустим, наши эксперты проголосовали друг за друга следующим образом:
По данным этой матрицы вычисляются коэффициенты компетентности экспертов:
ki = 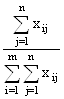
Вычислим коэффициенты компетентности экспертов для нашей задачи и результаты занесем в таблицу:
Крайний правый столбец – это коэффициенты компетентности экспертов. Они уже были использованы в примере группового выбора, рассмотренного выше.
Раздел 7. Критерии модульного оценивания знаний
Кредитно-модульная система – это модель организации учебного процесса, которая основывается на объединении двух составляющих: модульной технологии обучения и кредитов (зачетных единиц) и охватывает содержание, формы контроля качества знаний, навыков и учебной деятельности студента в процессе аудиторной и самостоятельной работы.
Рейтинговая система оценивания – это система определения качества выполненной студентом всех видов аудиторной и самостоятельной работы и уровня приобретенных им знаний и навыков путем оценивания в баллах результатов этой работы во время текущего модульного и полусеместрового итогового контроля, с последующим переведением рейтинговой оценки в баллах в оценки традиционной национальной шкалы и шкалы ECTS.
Рейтинговая оценка состоит из баллов, которые студент получает за определенную учебную деятельность на протяжении усвоения данного модуля – тестирование, выполнение и защита индивидуальных задач (домашних контрольных работ), выполнение аудиторной самостоятельной работы и выступления на практических занятиях и т.п..
Семестровый курс дисциплины "Теория принятия решений" разбит на 4 модуля. В конце каждого модуля проводится модульный контроль в виде аудиторной контрольной работы (АКР) или защиты домашней контрольной работы (ДКР), который оценивается до 25 баллов.
Для модуля №1 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- аудиторная контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Для модуля №2 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- аудиторная контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Для модуля №3 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- домашняя контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Для модуля №4 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- аудиторная контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Общая балльная оценка за полусеместр выводится простой суммой полученных студентом баллов за все модули полусеместра. Максимальная полусеместровая оценка составляет 100 баллов. Оценка по национальной шкале выводится в соответствии с таблицей:
| Итоговый рейтинговый балл по дисциплине | Оценка по шкале ECTS | Оценка по национальной шкале |
| 91-100 | A | Отлично |
| 81-90 | B | Хорошо |
| 76-80 | C | |
| 61-75 | D | Удовлетворительно |
| 51-60 | E | |
| 21-50 | FX | Неудовлетворительно |
| 0-20 | F |
Раздел 8. Задания для самостоятельной работы студентов 8.1 Домашняя контрольная работа
Согласно рабочей учебной программе дисциплины "Теория принятия решений" в модуле №3 выполняется домашняя контрольная работа.
Цель домашней контрольной работы – детальная и более тщательная проработка лекционного и практического материала, с целью проверки и контроля степени его усвоения, формирование у студентов предусмотренных рабочей программой навыков.
Домашняя контрольная работа выполняется на бумажных носителях.
Домашняя контрольная работа содержит 30 вариантов. Каждый вариант содержит четыре задания:
- задание №1 – решение матричной игры в чистых стратегиях;
- задание №2 – решение матричной игры в смешанных стратегиях симплекс-методом;
- задание №3 – решение матричной игры в смешанных стратегиях графическим методом.
Студент выбирает вариант домашней контрольной работы согласно своему порядковому номеру в журнале списка своей группы. Контрольная работа, не соответствующая своему варианту, не проверяется и к защите не допускается.
Задание №1.
Определить оптимальные чистые стратегии и цену игры:
1 вариант 2 вариант 3 вариант



4 вариант 5 вариант 6 вариант



7 вариант 8 вариант 9 вариант



10 вариант 11 вариант 12 вариант



13 вариант 14 вариант 15 вариант



16 вариант 17 вариант 18 вариант



19 вариант 20 вариант 21 вариант



22 вариант 23 вариант 24 вариант



25 вариант 26 вариант 27 вариант



28 вариант 29 вариант 30 вариант



Задание №2.
Определить симплекс-методом оптимальные смешанные стратегии и цену игры:
1 вариант 2 вариант 3 вариант



4 вариант 5 вариант 6 вариант



7 вариант 8 вариант 9 вариант



10 вариант 11 вариант 12 вариант



13 вариант 14 вариант 15 вариант



16 вариант 17 вариант 18 вариант



19 вариант 20 вариант 21 вариант



22 вариант 23 вариант 24 вариант



25 вариант 26 вариант 27 вариант



28 вариант 29 вариант 30 вариант



Задание №3.
Определить графическим методом оптимальные смешанные стратегии и цену игры:
1 вариант 2 вариант 3 вариант
![]()
![]()
![]()
4 вариант 5 вариант 6 вариант
![]()
![]()
![]()
7 вариант 8 вариант 9 вариант
![]()
![]()
![]()
10 вариант 11 вариант 12 вариант
![]()
![]()
![]()
13 вариант 14 вариант 15 вариант
![]()
![]()
![]()
16 вариант 17 вариант 18 вариант
![]()
![]()
![]()
19 вариант 20 вариант 21 вариант
![]()
![]()
![]()
22 вариант 23 вариант 24 вариант
![]()
![]()
![]()
25 вариант 26 вариант 27 вариант
![]()
![]()
![]()
28 вариант 29 вариант 30 вариант
![]()
![]()
![]()
Общие вопросы к всем модулям:
1. Что такое исследование операций?
2. Что такое ЛПР?
3. Что такое математическая модель?
4. Что такое переменные?
5. Что такое альтернатива?
6. Что такое план?
7. Что такое ограничение?
8. Что такое допустимое множество?
9. Что такое допустимый план?
10. Что такое целевая функция?
11. Что такое оптимальный план?
12. Что такое математическое моделирование?
13. Что такое математическое программирование?
14. Что такое линейное программирование?
15. Что такое целочисленное программирование?
16. Что такое динамическое программирование?
17. Что такое нелинейное программирование?
18. Что такое задача принятия решения?
19. Что такое бинарные отношения?
20. Что такое ориентированный граф?
21. Что такое множество Парето?
22. Найти множество Парето.
23. Что такое принятие решения в условиях определенности?
Вопросы к модулю №1:
24. Что такое принятие решения в условиях риска?
25. Какие условия использования критерия Байеса?
26. Решить задачу с помощью критерия Байеса.
27. Какие условия использования критерия Лапласа?
28. Решить задачу с помощью критерия Лапласа.
29. Какие условия использования критерия Гермейера?
30. Решить задачу с помощью критерия Гермейера.
31. Какие условия использования критерия Ходжа-Лемана?
32. Решить задачу с помощью критерия Ходжа-Лемана.
Воп росы к модулю №2:
33. Что такое принятие решения в условиях неопределенности?
34. Какие условия использования принципа максимина?
35. Решить задачу с помощью принципа максимина.
36. Какие условия использования критерия азартного игрока?
37. Решить задачу с помощью критерия азартного игрока.
38. Какие условия использования критерия произведений?
39. Решить задачу с помощью критерия произведений.
40. Какие условия использования критерия Севиджа?
41. Решить задачу с помощью критерия Севиджа.
42. Какие условия использования критерия Гурвица?
43. Решить задачу с помощью критерия Гурвица.
Вопросы к модулю №4:
44. Что такое принятие решения в условиях противодействия?
45. Что такое матричная игра?
46. Что такое платежи матричной игры?
47. Что такое матрица платежей?
48. Что такое матричная игра с нулевой суммой?
49. Что такое матричная игра с ненулевой суммой?
50. Что такое седловая точка?
51. Что такое чистая стратегия?
52. Что такое смешанная стратегия?
53. Найти седловую точку матрицы.
54. Решить матричную игру в чистых стратегиях.
55. Найти множество Парето для задачи двукритериального выбора.
56. Решить задачу многокритериального выбора методом линейной аддитивной свертки.
57. Решить задачу многокритериального выбора методом мультипликативной свертки.
58. Решить задачу многокритериального выбора методом максиминной свертки.
59. Решить задачу про групповую экспертную оценку.
60. Решить задачу экспертной оценки объектов с учетом компетентности экспертов.
8.3 Контрольные вопросы к экзамену по дисциплине1. Исследование операций как наука о принятии оптимальных решений.
2. Построение математической модели.
3. Математическое программирование. (Общий обзор, основные понятия, классы задач.)
4. Принятие решения: постановка задачи, возможные случаи.
5. Принятие решений в условиях риска. Критерий Байеса.
6. Принятие решений в условиях риска. Критерий Лапласа.
7. Принятие решений в условиях риска. Критерий Гермейера.
8. Принятие решений в условиях риска. Критерий Ходжа-Лемана.
9. Принятие решений в условиях неопределенности. Принцип максимина.
10. Принятие решений в условиях неопределенности. Критерий азартного игрока.
11. Принятие решений в условиях неопределенности. Критерий произведений.
12. Принятие решений в условиях неопределенности. Критерий Севиджа.
13. Принятие решений в условиях неопределенности. Критерий Гурвица.
14. Принятие решений в условиях противодействия. Общие понятия.
15. Матричные игры.
16. Чистые стратегии, седловая точка, цена игры.
17. Смешанные стратегии.
18. Представление матричной игры в виде задачи линейного программирования.
19. Графический метод решения матричной игры.
20. Принятие решений в условиях нескольких критериев выбора (многокритериальный выбор).
21. Линейные свёртки.
22. Максиминная и лексикографическая свёртки.
23. Мультипликативные свёртки.
24. Описание выбора на языке бинарных отношений.
25. Множество Парето. Максимальный элемент.
26. Матрицы смежности и инцидентности.
27. Принятие корпоративных решений.
28. Компетентность экспертов.
Контрольные экзаменационные вопросы используются в случае сдачи студентом экзамена по дисциплине на повышенную оценку в сравнении с оценкой, которую он получил по рейтингу полусеместра. В соответствии с действующим "Положением о кредитно-модульной системе организации учебного процесса и рейтинговом оценивании знаний студентов ЗГИА" оценка, которая получена на экзамене является окончательной и именно она вносится в экзаменационную ведомость и индивидуальный план (зачетную книжку) студента.
Учебно-методический материал по дисциплине
Основная литература (имеется в наличии в библиотеке ЗГИА)
1.Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для вузов. - М.: Высшая школа , 1986. - 319 c.
2.Волков И.К., Загоруйко Е.А. Исследование операций: Учебник для втузов / Ред. Зарубин В.В., Крищенко А.П. - 2-е изд. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. - 435 c.
3.Евланов В.Г. Теория и практика принятия решений. – М.: Экономика, 1984. – 175 с.
4.Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения. – М.: Радио и связь, 1981. – 560 с.
5.Колпаков В.М. Теория и практика принятия управленческих решений: Учеб. пособие для вузов. – К.: МАУП, 2000. – 254 с.
6.Костевич Л.С., Лапко А.А. Теория игр. Исследование операций: Учеб. пособие для вузов. - Мн.: Вышэйшая школа, 1982. - 230 c.
7.Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование: Учеб. пособие для вузов - М.: Высшая школа , 1976. - 350 c.
8.Мулен Э. Кооперативное принятие решений: Аксиомы и модели. - М.: Мир, 1991. - 463c.
9.Таха Хемди А. Введение в исследование операций, 7-е изд: Пер. с англ. – М.: Изд. дом "Вильямс", 2005. – 912 с.
10.Теория выбора и принятия решений Учеб. пособие для вузов. - М.: Наука, 1982. - 328 c.
11.Тоценко В.Г. Методы и системы поддержки принятия решений: Алгоритмический аспект / НАН Украины. Ин-т пробл. регистрации информ. - К.: Наук. думка, 2002. – 381 c.
12.Трухаев Р.И. Модели принятия решений в условиях неопределенности / АН СССР. Дальневост. науч. центр. Хабаров. комплекс НИИ. - М.: Наука, 1981. - 257 c.
Дополнительная литература
13.Вентцель Е.С. Исследование операций. – М.: Советское радио, 1972.
14.Гафт М.Г., Подиновский В.В. О построении решающих правил в задачах принятия решений. - Автоматика и телемеханика, №6, 1981.
15.Джексон П. Введение в экспертные системы: Пер. с англ.: Учеб. пособие. – М.: Изд. дом "Вильямс", 2001.
16.Ершов А.Т., Карандаев И.С., Статкус А.В. Матричные игры и графы. – М.: МИУ, 1986.
17.Ларичев О.И. Наука и искусство принятия решений. – М.: Наука, 1979.
18.Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. – М.: Логос, 2003.
19.Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2002. – 240с.
20.Фон Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. – М.: Наука, 1970.
21.Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВ-Петербург, 2005. – 416 с.
Похожие работы
... , чем обычно. Общий заработок в 1000 $ они должны поделить следующим образом: певцу 350 $, пианисту 435 $, ударнику 175 $. Глава . Принятие решений в условиях частичной неопределенности. Элементы теории статистических решений. Предметом рассмотрения данного раздела служат статистические модели приянятия решений, трактуемые как статистические игры или игры с природой при использовании ...
митационной модели , проведение экспериментов на этих моделях Обработка результатов экспериментов с целью выбора наилучшего варианта модернизации или реорганизации сети Проведение работы по модернизации и реорганизации сети Требования к специалисту на должность администратора сети Приведем некоторые примеры требований: Работодатель №1: Опыт построения и сопровождения программных/аппаратных ...
... максимизирующий выделенный критерий на множестве исходов, оценки которых по остальным критериям не ниже назначенных. Всякие задачи принятия решения является: Альтернативы (варианты, планы, допустимые альтернативы) Исходы (Результаты) Оптимальные решения (Наилучшие решения) Математическая модель ЗПР включает в себя формальное описание этих компонентов. X - множество допустимых альтернатив A ...
... , среднее распределение процентных отношений, дисперсия, стандартные отклонения, коэффициенты вариации Коэффициенты – j, c2, Чупрова, Спирмена, коэффициент корреляции Пирсона 2. Теория принятия решений Выбор любого управленческого решения всегда ограничен. Это объясняется необходимостью следовать определённым нормам поведения, которые и ориентируют руководителя. В зависимости от ...
0 комментариев