Навигация
Описання алгоритму та засобів, які будуть використовуватися
2. Описання алгоритму та засобів, які будуть використовуватися
При виконанні даної курсової роботи буде проводитись статистичний аналіз.
Статистичний аналіз, який виконується з метою визначення залежностей між метриками, складається з трьох етапів: первинний статистичний аналіз, кореляційний аналіз та регресійний аналіз.
Схема побудови залежностей між метриками представлена на рис. 1.
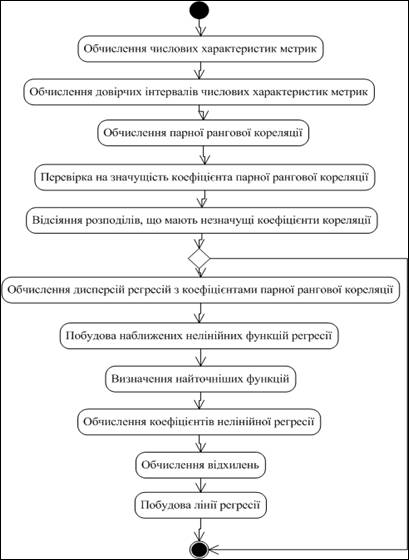
Рис. 1 Схема побудови залежностей
Первинний статистичний аналіз метрик та експертних оцінок
Метою первинного статистичного аналізу являється визначення закону розподілу випадкової величини, точніше визначення відповіді на питання „Чи є даний закон розподілу випадкової величини нормальним?”. На етапі первинного статистичного аналізу відбувається дослідження вхідних статистичних даних. Спочатку аналізуються метрики, отримані в результаті вимірювання набору програм, далі експертні оцінки, що зробили експерти для цього ж набору програм.
Кінцевою метою первинного статистичного аналізу є визначення, чи належить побудований закон до нормального. Причиною цього є те, що подальший аналіз базується на перевірці на „нормальність” закону розподілу, тобто кожний з наступних етапів починається цією перевіркою, і в залежності від відповіді застосовуються різні методи обчислень.
Кореляційний аналіз пар „метрика – експертна оцінка”
На етапі кореляційного аналізу визначається, чи існує залежність між певними метриками та експертними оцінками, чи її немає. Якщо залежність існує, то проводиться первинна обробка даних для визначення довірчої ймовірності та виду залежності. В іншому випадку робиться висновок про відсутність залежності.
Отже, результатом даного етапу є відсіювання незалежних між собою пар „метрика – експертна оцінка” та визначення за можливістю виду залежності для інших пар.
Регресійний аналіз залежних величин
Регресійний аналіз – останній етап в дослідженні на залежність метрик та експертних оцінок. Він проводиться тільки при виконанні умови, що дисперсія залежної змінної (експертної оцінки) повинна залишатися постійною при зміні значення аргументу (метрики), тобто, спочатку визначається дисперсія експертної оцінки для кожного прийнятого значення метрики.
Якщо пара „метрика – експертна оцінка” пройшла всі етапи і не була відсіяною, робиться висновок, що експертна оцінка залежить певним чином від значення метрики з силою, що показує коефіцієнт детермінації, а вигляд залежності визначає лінія регресії.
3. Первинний статистичний аналіз із гістограмами метрик, експертної оцінки властивості ПЗ та основними статистичними характеристиками, та перевірками
Первинний статистичний аналіз проводиться за допомогою програми Statistica, що набагато спрощує обчислення.
Важливим способом "опису" змінної є форма її розподілу, яка показує, з якою частотою значення змінної потрапляють в певні інтервали. Ці інтервали, що називаються інтервалами угруповання, обираються дослідником. Зазвичай дослідника цікавить, наскільки точно розподіл можна апроксимувати нормальним (див. нижче картинку з прикладом такого розподілу) (див. також Елементарні поняття статистики). Прості описові статистики дають про це деяку інформацію. Наприклад, якщо асиметрія (показує відхилення розподілу від симетричного) істотно відрізняється від 0, то розподіл несиметрично, у той час як нормальний розподіл абсолютно симетрично. Отже, у симетричного розподілу асиметрія дорівнює 0. Асиметрія розподілу з довгим правим хвостом позитивна. Якщо розподіл має довгий лівий хвіст, то його асиметрія негативна. Далі, якщо ексцес (показує "гостроту піку" розподілу) істотно відрізняється від 0, то розподіл має або більше закруглений пік, ніж нормальне, або, навпаки, має більш гострий пік (можливо, є декілька піків). Зазвичай, якщо ексцес позитивний, то пік загострений, якщо негативний, то пік закруглений. Ексцес нормального розподілу дорівнює 0.
Більш точну інформацію про форму розподілу можна отримати за допомогою критеріїв нормальності (наприклад, критерію Колмогорова-Смирнова або W критерію Шапіро-Уїлки). Однак жоден із цих критеріїв не може замінити візуальну перевірку за допомогою гістограми (графіка, що показує частоту влучень значень змінної в окремі інтервали).
Гістограма дозволяє "на око" оцінити нормальність емпіричного розподілу. На гістограму також накладається крива нормального розподілу. Гістограма дозволяє якісно оцінити різні характеристики розподілу. Наприклад, на ній можна побачити, що розподіл бімодальному (має 2 піку). Це може бути викликано, наприклад, тим, що вибірка неоднорідна, можливо, витягли з двох різних популяцій, кожна з яких більш-менш нормальна. У таких ситуаціях, щоб зрозуміти природу спостережуваних змінних, можна спробувати знайти якісний спосіб поділу вибірки на дві частини.
Кінцевою метою первинного статистичного аналізу є визначення, чи належить побудований закон до нормального. Причиною цього є те, що подальший аналіз базується на перевірці на „нормальність” закону розподілу, тобто кожний з наступних етапів починається цією перевіркою, і в залежності від відповіді застосовуються різні методи обчислень.
Статистичні дані, які були виміряні за допомогою програмного забезпечення Statistica подано в таблиці 4.
Таблиця 4. Статистичні дані
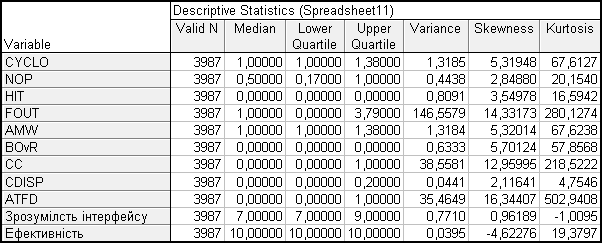
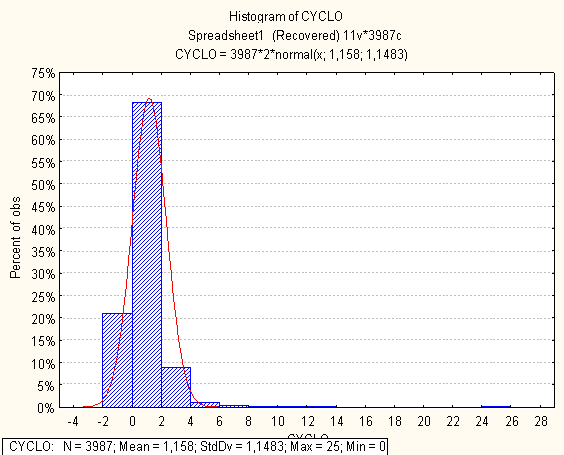
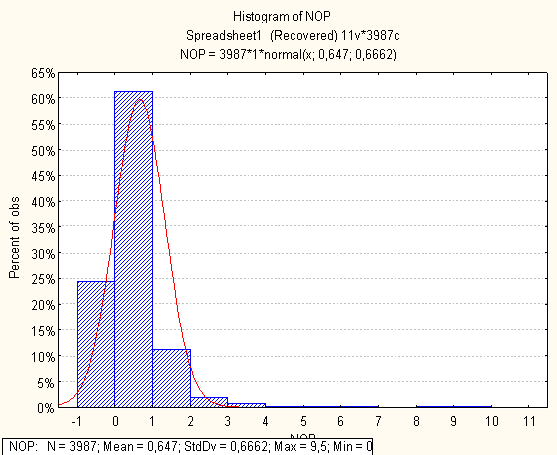
Нижче на малюнках подано побудовані гістограми по кожній метриці
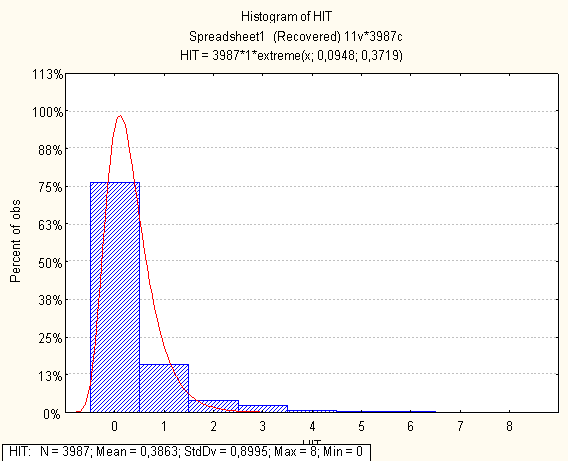
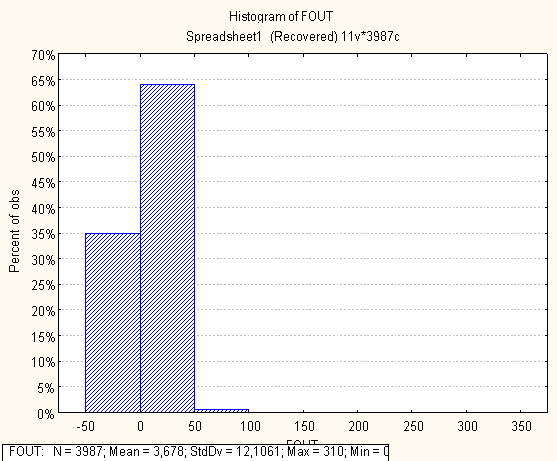

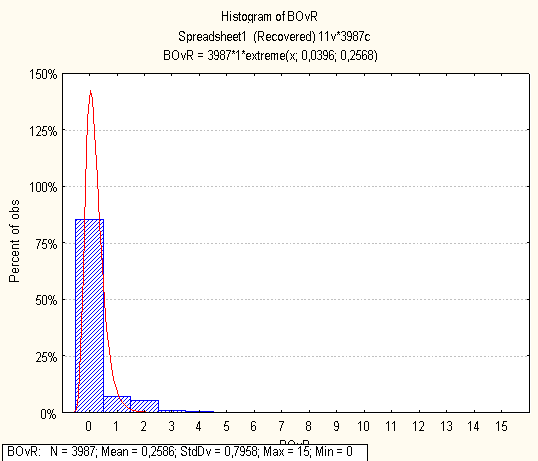
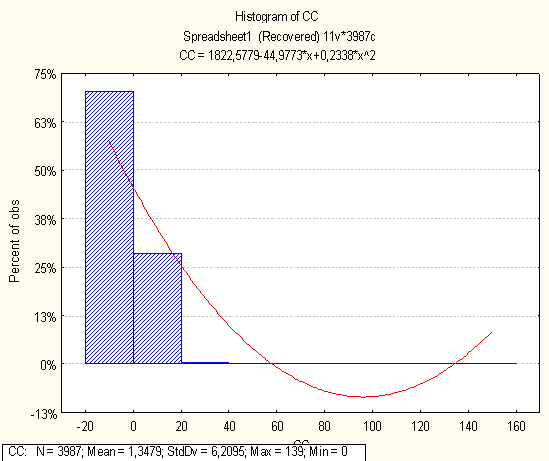
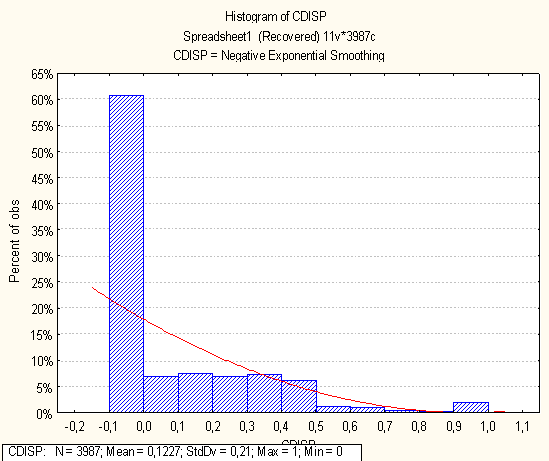
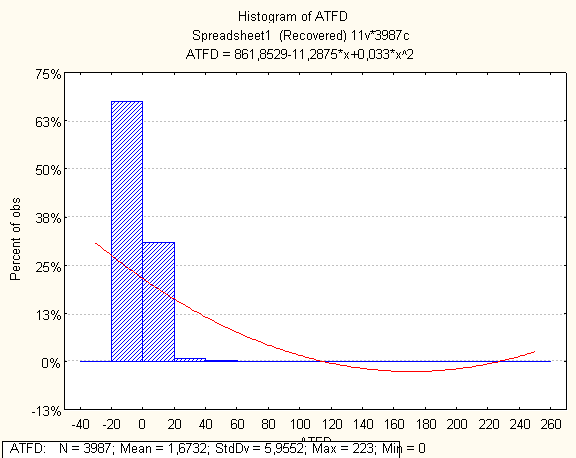
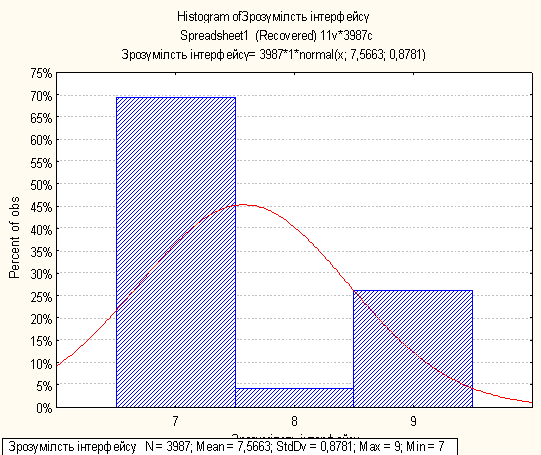
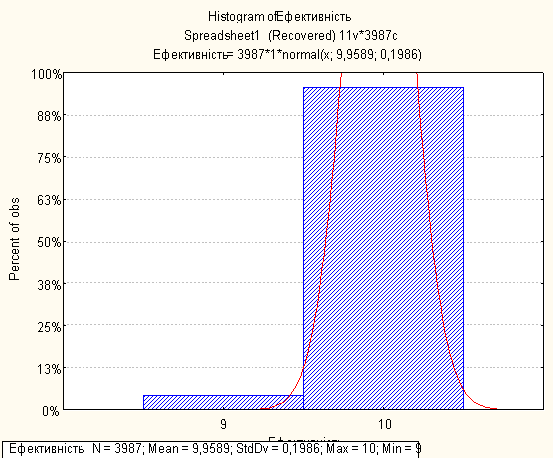
0 комментариев