Висновки по первинному статистичному аналізі

4.  Висновки по первинному статистичному аналізі

При проведенні первинного статистичного аналізу було обчислено статичні характеристики такі, як математичне сподівання, середнє квадратичне відхилення, коефіцієнт ексцесу та асиметрії, довірчі інтервали та визначено закони розподілу.

У відповідності до отриманих даних можна зробити наступні висновки:

Метрики з нормальним розподілом

-  CYCLO

-  NOP

-  FOUT

-  AMW

-  Ефективність(експертна оцінка)

Метрики з ненормальним розподілом

-  HIT

-  BOvR

-  CC

-  CDISP

-  ATFD

-  Зрозумілість інтерфейсу(експертна оцінка)

Ці дані будуть в подальшому використовуватись для кореляційного та регресійного аналізу.

5.  Кореляційний аналіз з кореляційними полями та розрахованими коефіцієнтами кореляції, та перевірками

Визначення кореляції. Кореляція являє собою міру залежності змінних. Найбільш відома кореляція Пірсона. При обчисленні кореляції Пірсона передбачається, що змінні виміряні, як мінімум, у інтервального шкалою. Деякі інші коефіцієнти кореляції можуть бути обчислені для менш інформативних шкал. Коефіцієнти кореляції змінюються в межах від -1.00 до +1.00. Зверніть увагу на крайні значення коефіцієнта кореляції. Значення -1.00 означає, що змінні мають строгу негативну кореляцію. Значення +1.00 означає, що змінні мають строгу позитивну кореляцію. Відзначимо, що значення 0.00 означає відсутність кореляції.

Негативна кореляція. Дві змінні можуть бути пов'язані таким чином, що при зростанні значень однієї з них значення іншої зменшуються. Це і показує негативний коефіцієнт кореляції. Про такі змінні говорять, що вони негативно корельовані.

Позитивна кореляція. Зв'язок між двома змінними може бути такою - коли значення однієї змінної зростають, значення іншої змінної також зростають. Це і показує позитивний коефіцієнт кореляції. Про такі змінні говорять, що вони позитивно корельовані.

Найбільш часто використовуваний коефіцієнт кореляції Пірсона r називається також лінійної кореляцією, тому що вимірює ступінь лінійних зв'язків між змінними.

Проста лінійна кореляція (Пірсона r). Кореляція Пірсона (далі називана просто кореляцією) припускає, що дві розглянуті перемінні виміряні в інтервальній шкалі. Вона визначає ступінь, з якою значення двох змінних "пропорційні" один одному. Важливо, що значення коефіцієнта кореляції не залежить від масштабу виміру. Наприклад, кореляція між ростом і вагою буде однієї і тієї ж, незалежно від того, проводилися виміри в дюймах і чи фунтах у сантиметрах і кілограмах. Пропорційність означає просто лінійну залежність. Кореляція висока, якщо на графіку залежність "можна представити" прямою лінією (з позитивним чи негативним кутом нахилу).

Помилкові кореляції. Грунтуючись на коефіцієнтах кореляції, ви не можете строго довести причинного залежності між змінними , однак можете визначити помилкові кореляції, тобто кореляції, які обумовлені впливами "інших", що залишаються за межами вашого поля зору змінних. Найкраще зрозуміти помилкові кореляції на простому прикладі. Відомо, що існує кореляція між шкодою, завданою пожежею, і кількістю пожежних, почали гасити пожежу. Однак ця кореляція нічого не говорить про те, наскільки зменшаться втрати, якщо буде викликано менше число пожежних. Причина в тому, що є третя змінна яка впливає як на заподіяний збиток, так і на число викликаних пожежників. Якщо ви будете "контролювати" цю змінну, то вихідна кореляція або зникне, або, можливо, навіть змінить свій знак. Основна проблема хибної кореляції полягає в тому, що ви не знаєте, хто є її агентом. Тим не менше, якщо ви знаєте, де шукати, то можна скористатися приватні кореляції, щоб контролювати (частково виключена) вплив певних змінних.

Кореляційний аналіз проводився за допомогою пакету Statistica. Отримані результати по кореляційному аналізу подано в таблиці 4.

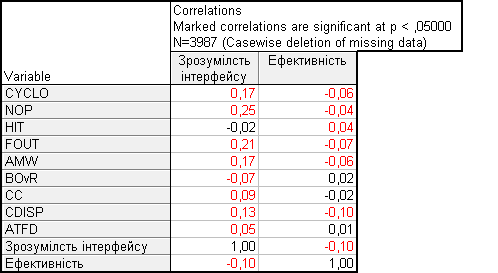
Таблиця 5. Результати кореляційного аналізу для пар прямі метрики-експертні оцінки, непрямі метрики-експертні оцінки

6.  Висновки по кореліційному аналізу

При проведенні кореляційного аналізу було за допомогою пакету Statistica обчислено коефіцієнти для пар метрика-експертна оцінка.

На основі отриманих даних, які подані в таблиці 4, можна зробити наступні висновки:

-  Значення коефіцієнтів кореляції для пар «метрика-експертна оцінка», що зображені червоним кольором вказують на залежність між метриками та експертною оцінкою

-  Значення коефіцієнтів кореляції для пар «метрика-експертна оцінка», що зображені чорним кольором не залежні між собою

-  Коефіцієнти кореляції не є дуже великим, що дає змогу сказати, що залежність між метриками та експертними оцінками, які досліджуються в данії курсовій роботі, не є значною.

Дані, що були отримані при проведені кореляційного аналізу, будуть використані з метою проведення регресійного аналізу.

7.  Регресійний аналіз з побудованими лініями регресій, визначеними функціями регресій, коефіцієнтами у функціях та перевірками

Загальне призначення множинної регресії (цей термін був вперше використаний в роботі Пірсона - Pearson, 1908) полягає в аналізі зв'язку між кількома незалежними змінними (званими також регрессорамі або предикторами) і залежною змінною. Наприклад, агент з продажу нерухомості міг би вносити в кожен елемент реєстру розмір будинку (у квадратних футів), кількість спалень, середній дохід населення в цьому районі відповідно до даних перепису і суб'єктивну оцінку привабливості будинку. Як тільки ця інформація зібрана для різних будинків, було б цікаво подивитися, чи пов'язані і яким чином ці характеристики будинку з ціною, за якою він був проданий. Наприклад, могло б виявитися, що кількість спальних кімнат є кращим пророкує фактором (предиктором) для ціни продажу будинку в деякому специфічному районі, ніж "привабливість" будинку (суб'єктивна оцінка). Могли б також виявитися і "викиди", тобто будинки, які могли б бути продані дорожче, з огляду на їхнє розташування і характеристики.

Фахівці з кадрів звичайно використовують процедури множинної регресії для визначення винагороди за адекватно виконану роботу. Можна визначити деяку кількість факторів або параметрів, таких, як "розмір відповідальності" (Resp) або "число підлеглих" (No_Super), які, як очікується, впливають на вартість роботи. Кадровий аналітик потім проводить дослідження розмірів окладів (Salary) серед порівнянних компаній на ринку, записуючи розмір платні та відповідні характеристики (тобто значення параметрів) по різних позиціях.

8.  Висновки по регресійному аналізу

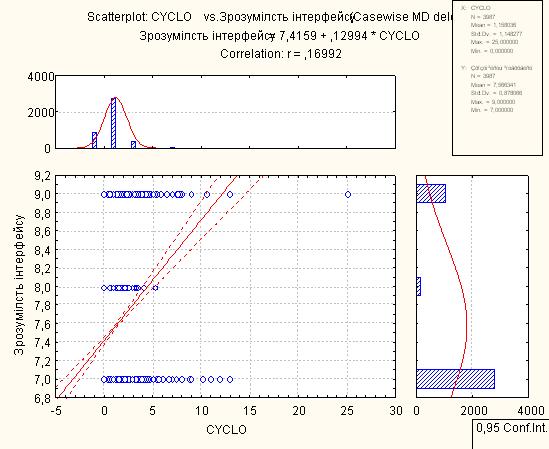
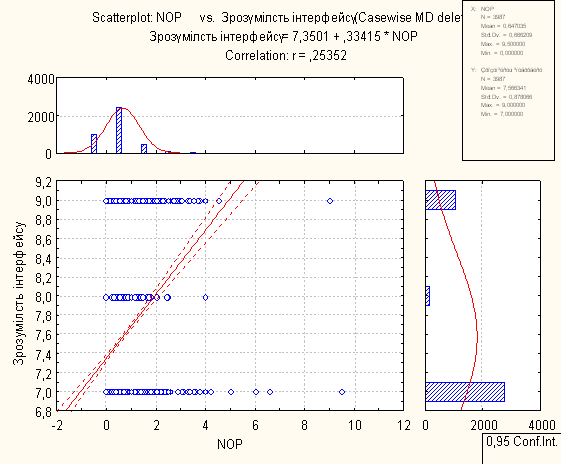
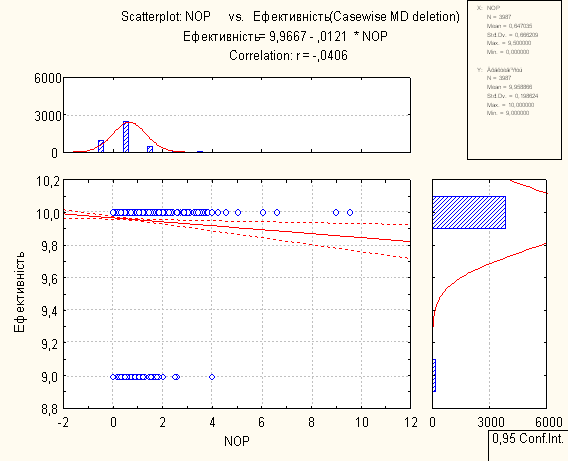
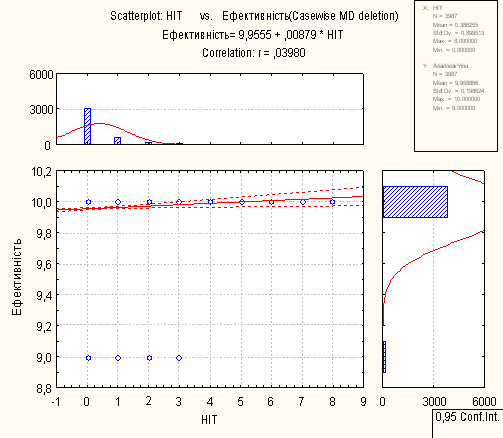
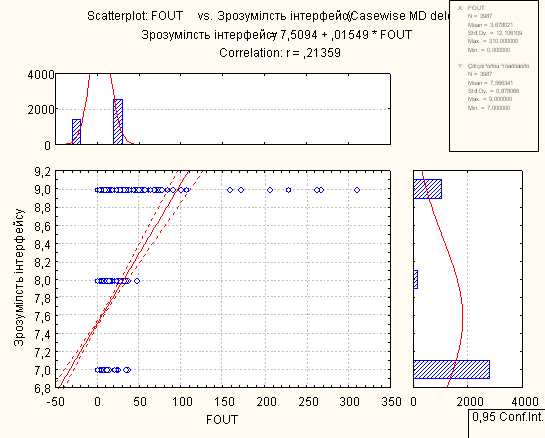
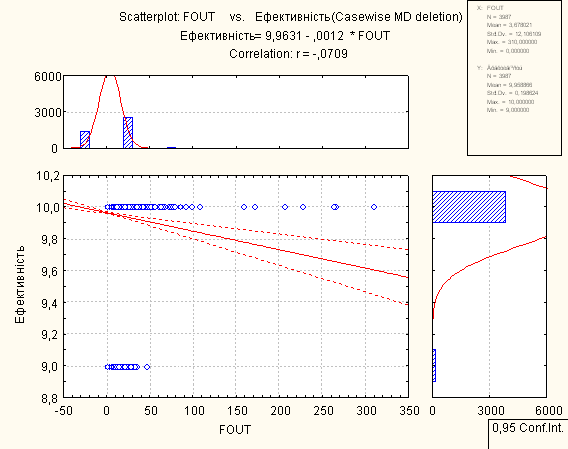
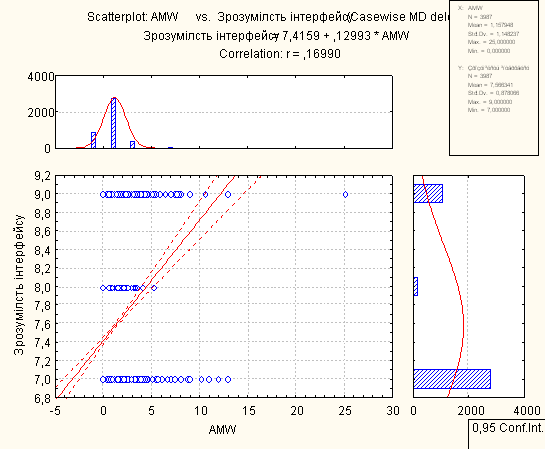
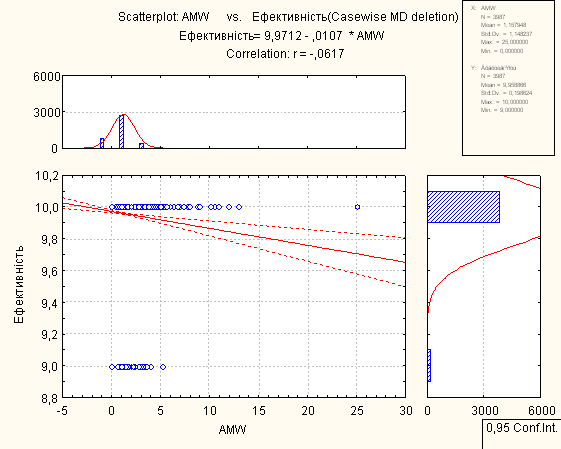
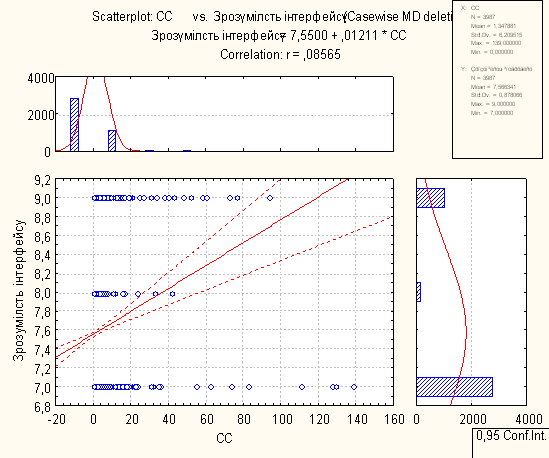
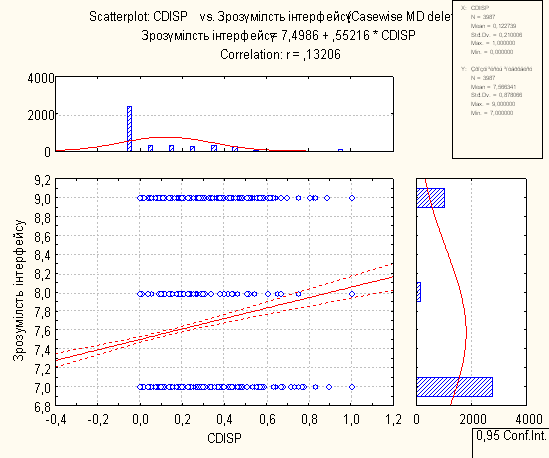
Для проведення регресійного аналізу був використаний пакет Statistica. За його допомогою було автоматично побудовано лінії регресії для пар метрика-експертна оцінка, визначено функції регресії.

На основі отриманих даних можна зробити наступні висновки:

-  В основному присутня лінійна регресія

-  З побудованих графіків можна зробити висновок, що переважна більшість пар «метрика-експертна» дуже слабо повязані.

9.  Загальні висновки

При виконанні даної курсової роботи було засвоєно теоретичні та практичні навички. На основі отриманих даних по первинному статичному, кореляційному та регресійному аналізі можна зробити наступні висновки:

Було визначено:

·  Метрики з нормальним розподілом

-  CYCLO

-  NOP

-  FOUT

-  AMW

-  Ефективність(експертна оцінка)

·  Метрики з ненормальним розподілом

-  HIT

-  BOvR

-  CC

-  CDISP

-  ATFD

-  Зрозумілість інтерфейсу(експертна оцінка)

Було оцінено значення отриманих коефіцієнтів кореляції

-  Коефіцієнти кореляції не є дуже великим, що дає змогу сказати, що залежність між метриками та експертними оцінками, які досліджуються в даній курсовій роботі, не є значними.

На основі регресійного аналізу можна зробити висновок, що :

-  В основному присутня лінійна регресія

-  Переважна більшість пар «метрика-експертна» дуже слабо повязані.