Багатокомпонентні оптичні системи. Еквівалентна фокусна відстань

4. Багатокомпонентні оптичні системи. Еквівалентна фокусна відстань

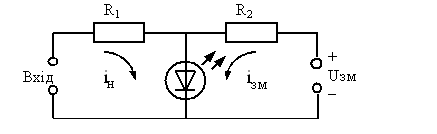
У практиці розрахунку оптичних систем велику роль відіграють двокомпонентні системи (рис. 9). Розглянемо дію такої системи за умови, що фокусні відстані компонентів і їхнє взаємне розташування відомі. Визначити положення фокальних і головних площин системи, що по своїй дії еквівалентна будь-якому числу заданих компонентів, можна шляхом розрахунку променів, рівнобіжних оптичний осі, у прямому і зворотному ході.

Послідовно застосовуючи формули кутів (21) і висот (24) для двокомпонентної системи, одержимо

tg s₁ = 0; tg s₂ = h₁Ф₁/n₂;

h₂ = h₁ [1 -(Ф₁/n₂ )d];

tg s = h₁ [].

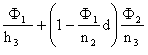Еквівалентна фокусна відстань системи

f¢ = h₁/tg s₃.

Тоді

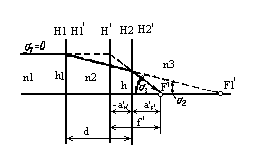
Рисунок 8- Система з двох компонентів

n₃/f¢ = Ф₁ + Ф₂ - (Ф₁Ф₂/n₂)d.

Відношення n₃/f є оптичною силою Ф усієї системи, тому

Ф = Ф₁ + Ф₂ - (Ф₁Ф₂/n₂)d. (25)

Відстань від другого компонента до еквівалентного заднього фокуса системи а'_F¢ = h₃/tgs₃, або

А¢_F' = f¢[1-(Ф₁/n₂ )d], (26)

а відстань від цього компонента до задньої головної площини системи

а¢_H¢ = а'_F¢ - f¢. (27)

З розрахунку ходу променя в зворотному ході, тобто з права на ліво, відповідно до формул (21) і (24) одержимо, що

-n/f = Ф = Ф_{1 +} Ф₂ – (Ф₁Ф₂/n₂)d;

a_F = f(1 - (Ф₂/n₂)d); (28)

a_H = a_F – f.

Якщо обидва компоненти оптичної системи знаходяться в однорідному середовищі, наприклад у повітрі, то

Ф = -1/f = 1/f¢ = Ф₁ + Ф₂ – Ф₁Ф₂d;

a_F = f(1- Ф₂d);

a_H = a_F - f;(29)

а¢_F¢ = f' (1 – Ф₁d);

a¢_H¢ = a¢_F¢ - f¢.

Для трикомпонентної системи, усі компоненти якої знаходяться в повітрі, еквівалентну оптичну силу Ф і відрізок а¢_F¢- визначають за такими формулами:

Ф = Ф₁ + Ф₂ + Фз - (Ф₂ + Фз) Ф₁d₁ - (Ф₁ + Ф₂ - Ф₁Ф₂d₁) Ф₃d₂;

a'_F¢ = (1/Ф) [1 – Ф₁ (d₁ + d₂) – Ф₂d₂ (1 – Ф₁d₁)].

Якщо в розглянутій системі компонента стикаються (d₁ = d₂ = 0), то оптична сила

Ф = Ф₁ + Ф₂ + Ф_з,

а відрізок а¢_F¢ дорівнює еквівалентній фокусній відстані системи f'.

Знайти параметри еквівалентної системи можна графічно шляхом побудови ходу променя, рівнобіжного оптичній осі, у прямому і зворотному напрямках.

5. Параксіальна область оптичної системи. Параксіальні і нульові промені

Реальні оптичні системи, що складаються зі сферичних і плоских заломлюючих і поверхонь, що відбивають, у загальному випадку не дають стигматичних зображень, тобто не задовольняють положенням ідеальної оптичної системи, Замість точкових зображень виходять кола розсіювання, Гомоцентричність пучка променів зберігається тільки за умови, що кути s і e, утворені реальними променями з оптичною віссю і з нормаллю до поверхні, нескінченно малі. При нескінченно малих кутах s, e, а отже, і s', e' справедливі такі вирази:

sin s/sin s' » s/s' = s'/s » const; (30)

для сферичної заломлюючої поверхні

n'/s' - n/s = (n' - n)/r: (31)

для плоскої заломлюючої поверхні

n'/s' - n/s = 0;(32)

для сферичної поверхні, що відбиває

l/s' + 1/s = 2/r. (33)

У виразах (30)-(33) відрізки s і s' визначають відповідно положення осьової предметної точки і її зображення щодо поверхні. Як видно з (30)-(33), відрізок s' залишається постійним для заданого відрізка s, тобто всі промені, що виходять із предметної точки під будь-якими, але малими кутами, після переломлення перетинаються в одній точці - точці зображення. Промені, що утворять малі кути s і s' з оптичною віссю і малі кути e й e' з нормаллю до заломлюючої поверхні, називають параксіальними променями, а область біля осі, усередині якої поширюються ці промені, - параксіальною областю. Кути s і s' для параксіальної області позначають a і a'. Співвідношення (31)-(38) називають рівняннями параксіальних променів і використовують для розрахунку ходу променів.

Для зручності виконання розрахунків вводиться поняття нульових променів. Нульовим променем називають фіктивний промінь, що переломлюється (віддзеркалюваний) так само, як і параксіальний, на поверхнях, але зустрічається з ними на кінцевих відстанях від оптичної осі і відтинає на оптичній осі ті ж відрізки, що і параксіальний промінь.

Шляхом розрахунку ходу нульового променя через оптичну систему визначають фокусні відстані і фокальні відрізки, а також положення зображення і лінійне збільшення системи для випадку, коли предмет знаходиться на кінцевій відстані.

Формули для розрахунку ходу нульового променя:

; (34)

₁h_k+1= h_k– d_k tg s_k+.₁

З виразу (34) одержимо формулу радіуса:

яку використовують для обчислення радіусів поверхонь при заданому ході променя. Для спрощення написання у формулах (34), (35) tg s рекомендується заміняти s.

6. Положення головних площин. Фокусні відстані заломлюючої поверхні в параксіальній області

У параксіальній області для реальних центрованих оптичних систем справедливі усі формули і положення ідеальної оптичної системи. Представимо малий предмет як би накладеним на поверхню в її вершини. Очевидно, що зображення цього предмета по положенню і розміру збігається із самим предметом. Отже, у вершині поверхні О (рис. 10) знаходиться сполучена пара сполучених точок, лінійне збільшення в який дорівнює одиниці, тобто, тут знаходяться співпадаючі головні точки заломлюючої поверхні. Головні площини збігаються і лежать у площині, дотичної до сфери в точці 0. Якщо предметну точку А переміщати уздовж оптичної осі так, щоб вона вилучилася в нескінченність, то точка А' збігається з заднім фокусом F' заломлюючої поверхні, тобто

s = -¥; s' = f'. (36)

Підставивши (36) у (31) і розв’язавши отриманий вираз відносно f', одержимо формулу для визначення задньої фокусної відстані заломлюючої поверхні:

f' = n'r/(n' - n). (37)

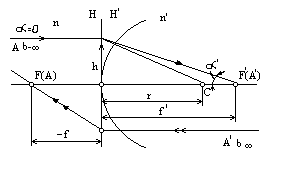
Рисунок 9- Схема для знаходження фокусних відстаней сферичної поверхні радіусом r

При переміщенні точки А' уздовж осі в нескінченність сполучена точка А збігається з переднім фокусом F поверхні, тобто

s = f;s' = ¥. (38)

З огляду на вираз (38), з формули (31) знайдемо вираз для передньої фокусної відстані сферичної поверхні:

f = nr/(n'- п). (39)

Розділивши (37) на (39), одержимо

f'/f = n'/n.(40)

Цей важливий вираз записано тут для однієї заломлюючої поверхні, але воно справедливо і для будь-якої складної оптичної системи.