Решение задачи о рассеянии на цилиндре

1.2 Решение задачи о рассеянии на цилиндре

Решается задача о нахождении полей на таком удалении от точек рассеяния, что фронт распространения волн этих полей можно считать плоскостью. Найдём для этого сперва общее решение, характеризующее бесконечно длинный цилиндр, а затем подставим в решение граничные условия, обобщив его тем самым на цилиндр длинны L.

Пусть поле падающих волн задаётся выражением:

, (1.2.1)

где  (см. рис. 2.1), падающая волна раскладывается в суперпозицию двух поляризаций – горизонтальной линейной и вертикальной линейной, а  и  горизонтальный и вертикальный вектора поляризации.

Падающая волна также может быть представлена в виде векторных цилиндрических волн, т.е. следующим образом:

. (1.2.2)

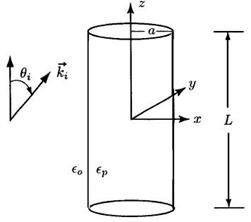
Цилиндр высоты L, радиуса a и проницаемости

Общее решение будет состоять из выражений для рассеянного поля и поля внутри цилиндра объединённых граничными условиями. Запишем теперь выражения, определяющие рассеянное и внутренне поля с точностью до неизвестных коэффициентов , , ,на оговоренном ранее расстоянии от точки рассеяния

, (1.2.3)

, (1.2.4)

где ,  – символ, с помощью которого обозначается конфигурация функций Бесселя и Ханкеля для величин, перед которыми он стоит, а  – коэффициенты, получаемые с использованием преобразования Фурье от выражения (1.2.1)

,

известны для такого приближения.

Граничные условия задаются равенствами:

, (1.2.5)

, (1.2.6)

из которых можно путём преобразований получить следующие выражения

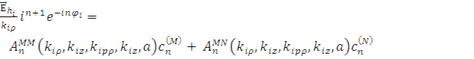, (1.2.7)

, (1.2.8)

которые задают зависимость неизвестных коэффициентов  из выражения для внутреннего поля (1.2.4) от направлений распространения , полей , , координаты  и  – радиуса цилиндра. Таким образом, поле определено, т. к. коэффициенты  могут быть легко получены из (1.2.7), (1.2.8).

Поле, образовавшееся после рассеяния падающего поля на цилиндре высоты L, в точках находящихся на достаточном для нашего приближения удалении определим путём интегрирования по конечной поверхности цилиндра, исключая граничные точки, используя формулу

. (1.2.9)

После подстановки (1.2.4) в (1.2.9) и выполнения интегрирования по dz в интервале ( и по dφ в интервале (0; 2π) получим следующее выражение для поля рассеянных волн:

{[

]

 [

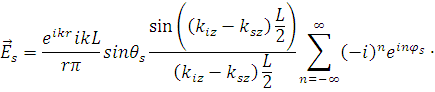
]}. (1.2.10)

Итак, нами были найдены поля  и . Однако есть несколько ограничений для полученных решений. Во-первых, следует иметь в виду, что такое решение непригодно вблизи точек рассеяния. Во-вторых, амплитудные коэффициенты, которые использовались в уравнениях (2.3), (2.4), были взяты готовыми, как известные для плоских волн. В общем случае их нужно рассчитывать отдельно для каждой конкретной задачи, используя преобразование Фурье, как это делается в работе [9].