Свойства маскирующих покрытий и требования, предъявляемые к ним

2.2 Свойства маскирующих покрытий и требования, предъявляемые к ним

Первое моделирование обтекания было проведено Каммером С.А. [5] в бесконечно длинной цилиндрической оболочке кругового сечения. Картина взаимодействия линейно поляризованной волны, вектор  которой параллелен оси цилиндра, с пространственно неоднородными компонентами проницаемостей покрытием показана на рисунке 2.2.1а. В этой модели были рассмотрены различные приближения.

Реальные покрытия имеют слоистую структуру, т.е. являются дискретными, что вызывает рассеяние, из-за которого траектории лучей вне оболочки перестают быть прямолинейными (рис. 2.2.1 б).

Идеальные параметры, использованные при построении графика 2.2.1а можно упростить. Если вектор  падающей волны параллелен оси цилиндра z, то задача становится двумерной и z – компоненты проницаемостей можно положить постоянными. Результат использования таких параметров отражен в графике 2.2.1в.

В маскирующем покрытии также присутствует частотная дисперсия , вследствие чего оно может быть полностью эффективным только на одной частоте, для которой компоненты проницаемостей имеют нужный вид. Ясно что чем меньше составляющие спектра поглощения оболочки в её рабочем диапазоне, тем лучше. Но поглощение в свою очередь зависит и от дисперсии. Так следствием из соотношений Крамерса-Кронига является большое поглощение в диапазоне частот, в котором эта среда проявляет сильные изменения дисперсии. Таким образом, чем более плавный вид имеют зависимости  и , тем меньше поглощение и тем ближе к идеалу эффект маскировки.

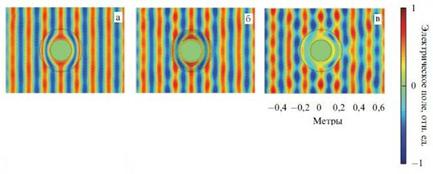
Распределение нормированной амплитуды электрического поля вблизи цилиндрической маскирующей оболочки

2.3 Разнообразие форм маскирующих покрытий

Сейчас скрытие уже теоретически осуществимо на оболочках произвольной двумерной формы, а именно в сечении трёхмерной модели. Рассмотрим их классификацию. Изначально рассматриваемый метод, как уже упоминалось, базировался на сферической оболочке (см. гл. 2 § 1). Дальнейшее развитие метода, как и следовало ожидать, привело к появлению многих других форм.

Одно из простейших покрытий с формой эллиптического цилиндра рассмотрено в работе [6].

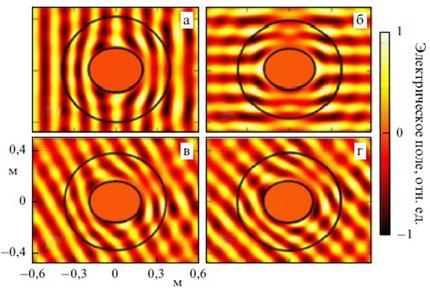
Распределение нормированной амплитуды электрического поля для различных углов падения излучения на эллиптическую оболочку: (а) 0°, (б) 90°, (в) 30°, (г) 45°

Для расчета его параметров используется линейное преобразование координат эллиптического цилиндра  , сжимающее сплошной эллиптический цилиндр в цилиндр с полостью:

, , . (2.3.1)

Направление падающего излучения для такой оболочки не безразлично из-за меньшей степени симметрии чем, например, у сферы. Из рисунка 2.3.1 видно, что поле после прохождения препятствия имеет наиболее близкую исходному структуру при нулевом угле падения излучения.

Произвольный цилиндр – оболочка-цилиндр с произвольным сечением. В общем случае не существует преобразования, переводящего произвольную односвязную область в подобную ей двусвязную. В таком случае  и  задают отдельно для каждой подобласти и используют отдельное преобразование для каждой из них. Например, цилиндрическая оболочка квадратного сечения (рис. 2.3.2), параметры которого рассчитаны в [7].

Для разбиения гладких оболочек на сектора их аппроксимируют кривыми Безье второго порядка. Эти кривые могут представлять собой любые канонические сечения (эллипсы, параболы, гиперболы), в зависимости от параметров. Для того чтобы достаточно точно аппроксимировать гладкую кривую, потребуется ломанная, состоящая из нескольких сотен отрезков, а кривых может понадобиться и две, как, например, для аппроксимации формы сердца. Параметрические уравнения кривой второго порядка по трём точкам  и трем параметрам (весам)  имеют вид [4]:

, (2.3.2)

. (2.3.3)

Кроме уже исследованной сферической формы оболочки из трёхмерных моделей появилась ещё и модель эллипсоида вращения [8]. Пока решения задачи о рассеянии на оболочках произвольной формы не найдено, что связано с трудностями моделирования таких задач.

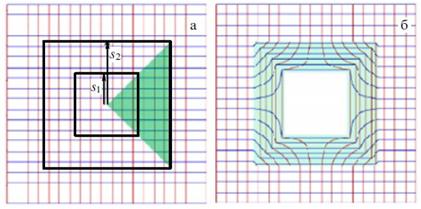
Координатное преобразование для цилиндрической оболочки квадратного сечения: для каждого сектора, выделенного на рисунке а, делается своё преобразование координат

Заключение

Итак, определившись с преобразованием координат для маскирующей оболочки, находим распределение её параметров  и . Затем, разложив при помощи БПФ падающую волну на элементарные плоские волны, определяем амплитудные коэффициенты. Далее, используя граничные условия, вычисляем поля распределения рассеянных волн и волн внутри рассеивателя. Найденные поля и есть решение поставленной задачи, которое в дальнейшем может быть также представлено графически. Варьируя изначальные параметры оболочки  и  можно тем самым приближать модель к реальным условиям и рассчитывать сечение рассеяния с учетом потерь и дисперсии материала.

В дальнейшем хотелось бы смоделировать решение для определённой оболочки, рассчитав её параметры, построить графики решений для этих оболочек. В дальней перспективе – написать программу, рассчитывающую сами поля, имея в качестве входящих значений параметры оболочки. Включить в неё функцию построения графиков решений. Подбирать оболочки и варьировать их параметры в поисках наиболее удачных.

Список литературы

1.  Leung Tsang, Jin Au Kong, Kung-Hau Ding «Scattering of electromagnetic waves: theories and applications», «A Wiley-lnterscience» (2000);

2.  W.H. Press, S.A. Teukolsky, W.T. Vetterling, Cambridge university press, New York (2002);

3.  Pendry J B, Schurig D, Smith D R Science 312 1780 (2006);

4.  А.Е. Дубинов, Л.А. Мытарева «Маскировки материальных объектов методом волнового обтекания», УФН (май 2010);

5.  Cummer S A et al. Phys. Rev. E 74 036621 (2006);

6.  Ma H et al. Phys. Rev. A 77 013825 (2008);

7.  Rahm Met al. Photon. Nanostruct. Fund. Appl. 6 87 (2008);

8.  Luo Y et al. Phys. Rev. B 78 125108 (2008);

9.  A VNovitsky, «Matrix approach for light scattering by bianisotropic cylindrical particles», J. Phys.: Condens. Matter 19 (2007);

10.  Г. Нуссбаумер, «Быстрое преобразование Фурье и алгоритмы вычисления свёрток», Москва, «Радио связь» (1985);