Навигация
Элементы практического применения теории массового обслуживания
2. Элементы практического применения теории массового обслуживания
Рассмотрим систему массового обслуживания на примере обслуживания рабочих необходимым инвентарем.Допустим, что в инвентарной кладовой работают два человека. Требуется определить, в какой степени они своевременно обеспечивают заявки на обслуживание, поступающие от рабочих; не обходятся ли простои рабочих в очереди дороже, чем дополнительное содержание еще одного или двух работников кладовой?
Таблица 1. – Расчет полного числа прихода рабочих в кладовую
| Число приходов в единицу времени (за 15 мин) | Наблюдаемое число приходов, % | Наблюдаемая частота приходов, % | Полное число приходов рабочих (гр.1 * гр.2) | Число приходов в единицу времени (за 15 мин) | Наблюдаемое число приходов, % | Наблюдаемая частота приходов, % | Полное число приходов рабочих (гр.1 * гр.2) |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 0 0 1 3 5 8 10 12 13 16 18 20 19 21 25 | 0 0 0,33 1,00 1,67 2,67 3,33 4,00 4,33 5,33 6,00 6,67 6,33 7,00 8,33 | 0 0 2 9 20 40 60 84 104 144 180 220 228 273 350 | 15 16 17 18 19 20 21 22 23 24 25 26 | 23 20 18 16 13 11 10 8 5 3 1 1 300 | 7,67 6,67 6,00 5,33 4,33 3,67 3,33 2,67 1,67 1,00 0,33 0,33 99,99 | 345 320 306 288 247 220 210 176 115 72 25 26 |
Для решения данной задачи необходимы прежде всего хронометражные замеры о потоке требований на обслуживание в единицу времени. Если хронометраж осуществляется в течение 10 дней каждые 15 минут за смену (кроме начала и конца рабочего дня), то за этот период времени было произведено 300 наблюдений (30 наблюдений, умноженное на 10 дней). Время наблюдений (T) составит 4500 мин (15 ×300). Причем таких промежутков, когда на склад никто не приходил или приходил только один рабочий, не наблюдалось, приход двух рабочих отмечался один раз, трех – три раза и т. д. (табл. 1).
Частота прихода двух рабочих при 300 наблюдениях равна 0,33![]() , трех – 1
, трех – 1![]() и т. д.
и т. д.
Для определения среднего числа приходов в единицу времени (![]() ) исчисляется полное число приходов (N) как сумма произведений числа приходов (количества пришедших в кладовую рабочих) на наблюдаемое число приходов.
) исчисляется полное число приходов (N) как сумма произведений числа приходов (количества пришедших в кладовую рабочих) на наблюдаемое число приходов.
Таким образом, среднее число требований на обслуживание, т. е. среднее число приходов в единицу времени (![]() ), составит:
), составит:
![]() =
=![]() =
=![]() =0,903 чел. – мин.
=0,903 чел. – мин.
Чтобы определить распределение вероятностей для длительности обслуживания при предположении, что закон распределения экспоненциальный, вычислим среднюю продолжительность одного обслуживания (Тобсл); она равна 1,6 мин.
После этого можно установить интенсивность обслуживания (![]() ):
):
![]() =
= ![]() ;
; ![]() =
=![]() =0,625 чел. – мин.
=0,625 чел. – мин.
В случае, когда ![]() <
<![]() , увеличение очереди не возникает, так как удовлетворение требований происходит не ранее их поступления. В данном примере
, увеличение очереди не возникает, так как удовлетворение требований происходит не ранее их поступления. В данном примере ![]() >
>![]() (0,903>0,625) и в кладовой образуется очередь.
(0,903>0,625) и в кладовой образуется очередь.
Точно определить величину очереди как случайную нельзя. Можно вычислить вероятность того, что в момент времени (t) очередь будет характеризоваться числом требований Pn(t):
Pn(t)=![]() (1-
(1-![]() ); P0(t) =(1-
); P0(t) =(1-![]() );
); ![]() =
=![]() ,
,
где P0(t) – вероятность отсутствия очереди.
В тех случаях, когда ![]()
![]() 1, вероятность отсутствия очереди (
1, вероятность отсутствия очереди (![]() 0) обычно берется из графиков (в данном примере
0) обычно берется из графиков (в данном примере ![]() =1,445).
=1,445).
Для построения таких графиков воспользуемся таблицей значений Р0 для различных значений ![]() и n (n –количество кладовщиков в инструментальной кладовой).
и n (n –количество кладовщиков в инструментальной кладовой).
Таблица 2. – Значения Р0 для различных значений ![]() и n
и n
|
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 1 2 3 4 | 0,33 | 0,363 0,111 | 0,367 0,130 0,037 | 0,367 0,134 0,046 0,013 | 0,367 0,135 0,049 0,016 | 0,367 0,135 0,049 0,017 | 0,368 0,135 0,050 0,018 |
По данным табл.2 , в данном случае рассматривается многолинейная система, когда n ![]() 1 (количество кладовщиков превышает единицу).
1 (количество кладовщиков превышает единицу).
Определим среднее время ожидания (Tс), которе складывается из среднего времени ожидания обслуживания в очереди (Тож) и среднего времени обслуживания (Тобсл):
Tс= Тож + Тобсл.
В том случае, когда в системе работает n кладовщиков, среднее время ожидания в очереди определяется по формуле при n =2:
Тож =  =
=![]() = 1,613;
= 1,613;
Tс = 1,613+1,6=3,213 мин;
при n=3
Тож =  =
=![]() = 0,199;
= 0,199;
Tс = 0,199 +1,6 =1,799 мин;
при n=4
Тож = 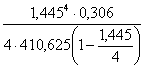 =
=![]() = 0,035;
= 0,035;
Tс = 0,035 +1,6 =1,635 мин и т. д.
Предположим, что у рабочего потери от простоев составляют 5, а содержание кладовщика – 4 ден. ед. в единицу времени. За период времени Т в систему поступает ![]() Т заявок, т. е. 1,445Т заявок.
Т заявок, т. е. 1,445Т заявок.
Потери вследствие простоя рабочих при различном числе кладовщиков, расходы на заработную плату кладовщиков, а также суммарные затраты и потери приведены в табл.3.
Таблица 3
| Количество кладовщиков | Потери от простоя Рабочих | Затраты на содержание кладовщиков | Суммарные затраты и потери |
| 2 3 4 | 3,213*1,445*5Т=23,214 Т 1,799*1,445*5Т=12,998Т 1,635*1,445*5Т=11,813Т | 8Т 12Т 16Т | 31,214Т 24,998Т 27,813Т |
Из табл. 3 следует, что экономически выгоднее в инструментальной кладовой иметь трех кладовщиков, поскольку суммарные затраты будут наименьшими (min 24,998Т).
Выводы
В процессе исследования были рассмотрены теоретические аспекты следующих методов программирования: динамическое программирование, сетевое планирование и управление, моделирование систем массового обслуживания, теория игр. Были рассмотрены основные задачи, решаемые с помощью этих методов, их основные достоинства и недостатки, а также основные понятия и теоремы. Динамическое программирование представляет собой математический аппарат, позволяющий осуществить оптимальное планирование многошаговых планируемых процессов и процессов, зависящих от времени. Предметом динамического планирования являются задачи оптимального планирования, носящие динамический характер в том смысле, что при их решении приходиться учитывать фактор времени или последовательность операций. Достоинством является то, что, используя поэтапное планирование, метод позволяет не только упростить решение задачи, но и решить те их них, к которым нельзя применить методы математического анализа. Недостатки: трудность решения многомерных задач, отсутствие универсального метода.
Сетевое планирование и управление представляет собой комплекс графических и расчетных методов, организационных мероприятий с целью моделирования, анализа и оптимизации плана работ по проектированию или изготовлению некоторого изделия. В основе лежит сетевой график, который является совершенной формой представления плана, которая значительно облегчает его восприятие и упрощает процесс руководства работами. Недостатки: не обеспечивает нахождение оптимального решения, не исключает влияния субъективных оценок.
Задача теории массового обслуживания состоит в выработке рекомендаций по рациональному построению систем массового обслуживания, рациональной организации их работы и регулирования потока заявок с целью обеспечения более высокой эффективности обслуживания при малых затратах на создание и функционирование системы. Метод дает оптимальный вариант обслуживания населения, при котором время обслуживания будет минимальным, качество – высоким, при этом не будет лишних затрат.
Теория игр – это теория математических моделей, интересы участников которых различны, причем они достигают своей цели различными путями. Теория игр дает рекомендации по рациональному образу действий участников многократно повторяющегося конфликта. Задачей теории игр является нахождение решения игры, т. е. определение для каждого игрока его оптимальной стратегии и цены игры.
В III главе приведена задача, которая решается с помощью теории массового обслуживания. Требовалось определить, своевременно ли обеспечиваются заявки на обслуживание, не обходятся ли простои рабочих в очереди дороже, чем затраты на содержание еще одного кладовщика. На основе хронометражных замеров определяется среднее число требований на обслуживание. Затем рассчитываются показатели среднего обслуживания одного работника и интенсивности обслуживания. Выясняем, что образуется очередь. Рассчитываем время ожидания обслуживания при различном числе кладовщиков (n=2,3,4,…). На основе таблицы затрат и потерь от простоя выясняем, что выгоднее содержать трех кладовщиков, т. к. затраты на их содержание будут больше, чем потери от простоя рабочих.
Литература
1. Баканов М.И., Шеремет А.Д. Теория экономического анализа: Учебник. – 4-е изд., доп. и перераб. – М.: Финансы и статистика, 1999
2. Браславец М.Е. Экономико – математические методы в организации и планировании сельскохозяйственного производства, 1974
3. Кравченко Р.Г., Попов И.Г., Толпекин С.З. Экономико – математические методы в организации и планировании сельскохозяйственного производства, 1974
4. Кузнецов Ю. Н., Кузубов В. И., Волощенко А. Б. Математическое программирование. Учебное пособие для ВУЗов. – М.: "Высшая школа", 1980.
Похожие работы
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
... 6. Петухов О.А. , Морозов А.В. , Петухова Е.О. Моделирование системное, имитационное, аналитическое. Учебное пособие – Санкт-Петербург 2008 7. Норенков И.П., Федорук Е.В.Имитационное моделирование систем массового обслуживания. Методические указания – Москва 1999 8. Кутузов О.И., Татарникова Т.М., Петров К.О. Распределенные информационные системы управления. Учебное пособие – Санкт-Петербург ...
... *0,1*25 – 1*,09 = 2148,2 ден.ед. Таким образом, максимальная прибыль достигается при установлении трех телефонных линий. Программа имитационного моделирования для оптимального режима работы примет вид: имитационный моделирование массовый обслуживание Результаты расчетов функциональных характеристик СМО: Характеристика Значение l 1/0,67 = 1,5 зв./мин. m 60/2=30 зв./мин. ...

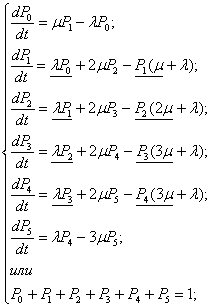




0 комментариев