Навигация
Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке
12342
знака
0
таблиц
10
изображений
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу 
в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
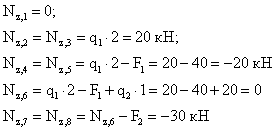
3. По найденным значениям строим эпюру .
Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные - под осью.
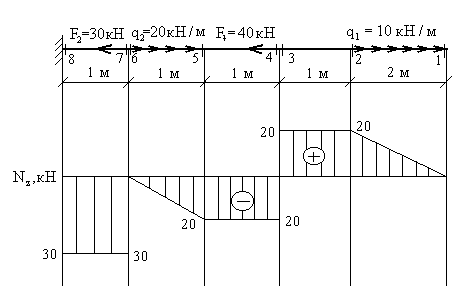
Рис. 4
Построение эпюр крутящих моментов
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.
Правило знаков для : условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным - в противном случае.
Пример 2. Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5,а).
Порядок расчета.
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.
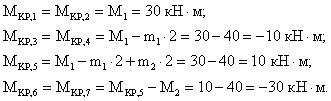
3.По найденным значениям строим эпюру (рис.5,б).
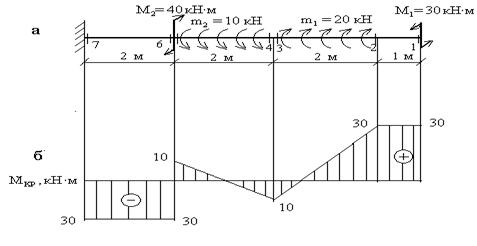
Рис. 5
Правила контроля эпюр
и Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.
1. Эпюры и всегда прямолинейные.
2. На участке, где нет распределенной нагрузки, эпюра () - прямая, параллельная оси; а на участке под распределенной нагрузкой - наклонная прямая.
3. Под точкой приложения сосредоточенной силы на эпюре обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре будет скачок на величину этого момента.
и изгибающих моментов 
в балках Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора - поперечная сила и изгибающий момент .
Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.
Правило знаков для : условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной - в противном случае.
Схематически это правило знаков можно представить в виде
Изгибающий момент в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.
Правило знаков для : условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной - в противном случае.
Схематически это правило знаков можно представить в виде:
Следует отметить, что при использовании правила знаков для в указанном виде, эпюра всегда оказывается построенной со стороны сжатых волокон балки.
При построении эпюр и в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.
Пример 3. Построить эпюры и (рис.6).
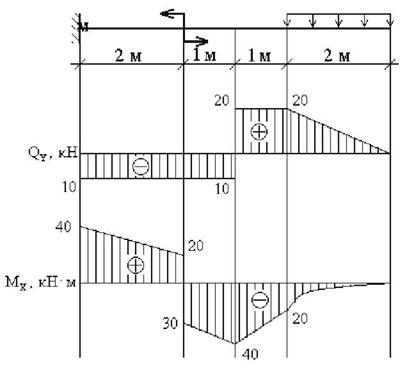
Рис. 6
Порядок расчета.
1. Намечаем характерные сечения.
2. Определяем поперечную силу в каждом характерном сечении.
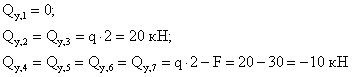
По вычисленным значениям строим эпюру .
3. Определяем изгибающий момент в каждом характерном сечении.
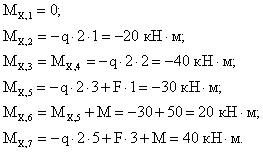
По вычисленным значениям строим эпюру , причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.
Указанные зависимости используются при построении эпюр 
, поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.
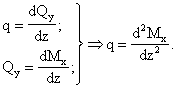
Пример 4. Построить эпюры (рис.7).
В данном случае для правильного построения эпюры необходимо использовать приведенные выше дифференциальные зависимости.
Порядок расчета.
1. Намечаем характерные сечения.
2. Определяем поперечные силы в характерных сечениях.
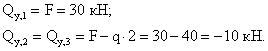
Строим эпюру .
Характер эпюры, то есть тот факт, что эпюра пересекает ось, говорит о том, что в этом сечении момент будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении 
, а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.
Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры разделить на интенсивность распределенной нагрузки q:
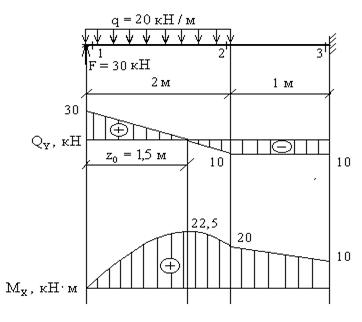
Рис. 7
Определяем изгибающие моменты в характерных сечениях.
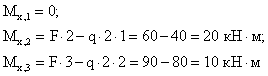
4. Вычисляем экстремальное значение изгибающего момента в сечении, где 
: 
Строим эпюру .
Литература:
1. Авдотьин Л.H., Лежава И.Г., Смоляр И.М. Градостроительное проектирование. Учебник для вузов. - М.: Стройиздат, 1989.
2. Архитектура гражданских и промышленны зданий. Т.2 «Основы проектирования» под ред. Предтеченского В.М. –М.: Стройиздат, 1976. 214 с.
3. Архитектура гражданских и промышленных зданий т.3 «Жилые здания» под ред. Шевцова К.К. –М.: Стройиздат, 1982. 239 с.
4. Архитектура гражданских и промышленных зданий т.5 «Промышленные здания» под ред. Шубина Л.Ф. –М.: Стройиздат, 1986. 239 с.
5. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: Общий курс. – М.: Стройиздат, 1991. - 768 с.
6. БНІП 2.02.01-83 Будівельні норми і правила. Норми проектування основ будівельників та споруд. М: Будвидав. 1985
7. Горохов В.А. и др. Инженерное благоустройство городских территорий, М.: Стройиздат, 1986.
8. Губень П.І. Проблеми ціноутворення в умовах ринкових відносин та шляхи їх подолання. – „Вісник Академії будівництва України”. 2000, № 8. с.19-22.
9. Долматов Б.І. Механіка грунтів, основи та фундаменти. – М. Будвидав, 1990
10. Дикман Л.Г. Организация и планирование строительного производства. – М.: Высшая школа, 1988. – 559 с.
Похожие работы
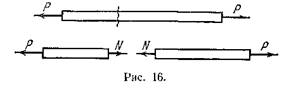
... процессов разрушения материалов или при исследовании поведения длинных и тонких стержней, для которых сжатие сопровождается, как правило, изгибом. Рассмотрим напряжения, возникающие в поперечном сечении растянутого стержня. Нормальная сила N является равнодействующей внутренних сил в сечении (рис. 17). Естественно предположить, что для однородного стержня внутренние силы распределены по ...
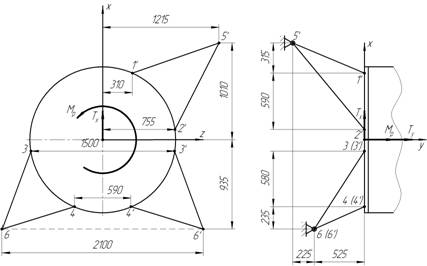
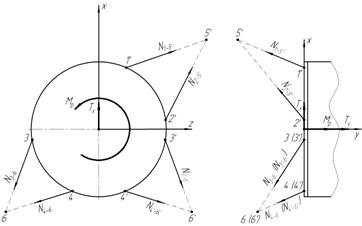
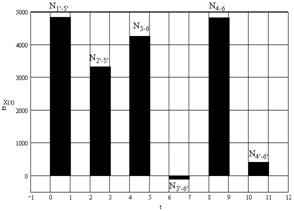
... 235 525 755 949.14 0.248 0.553 0.795 1.2 Расчетная схема фермы Расчетная схема фермы представлена на рисунке 1.2. Рисунок 1.2 – Расчетная схема подредукторной фермы вертолета 1.3 Определение усилий в стержнях фермы Составляем для данной статически определимой стержневой системы 6 уравнений равновесия: : После подстановки значений косинусов углов и сокращения на ...
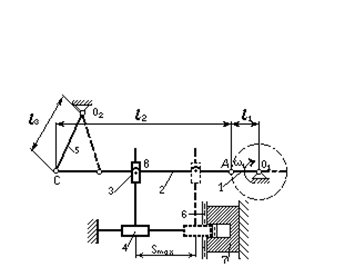
... характеристик решим графо-аналитическим методом, который основан на построении ряда последовательных положений звеньев механизма и соответствующих им планов скоростей. Механизм привода пресс-автомата с плавающим ползуном в масштабе μL=0,006 м/мм изобразим в двенадцати положениях. Положение механизма задаётся положением кривошипа 1. Каждое последующее положение кривошипа 1 отличается от ...
... представление о характере изменения силового фактора по длине или координате и позволяют установить местонахождение опасных сечений. 20. Сформулировать основные гипотезы и допущения, принятые в сопротивлении материалов. 1) Гипотеза о сплошном строении тела. 2) Гипотеза об идеальной упругости материала. 3) Гипотеза об однородности материала. 4) Гипотеза об изотропности материала. ...
0 комментариев