Навигация
Расчет собственной концентрации электронов и дырок
1. Расчет собственной концентрации электронов и дырок
![]() Е Е+dЕ
Е Е+dЕ
![]()
![]()
![]()
![]() Зона проводимости
Зона проводимости
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Е
Е
![]()
![]()
0 ![]()
![]()
![]() Е
Е![]()
- m
![]()
![]()
![]() Е
Е![]()
![]() -m¢
-m¢
Е![]()
Валентная зона.
Рис.1.Положение уровня Ферми в невырожденном полупроводнике.
На рис. 1 показана зонная структура невырожденного полупроводника. За нулевой уровень отсчета энергии принимают обычно дно зоны проводимости Е![]() . Так как для невырожденного газа уровень Ферми m должен располагаться ниже этого уровня, т.е. в запрещенной зоне, то m является величиной отрицательной (-m >>kT). При температуре Т, отличной от абсолютного нуля, в зоне проводимости находятся электроны, в валентной зоне – дырки. Обозначим их концентрацию соответственно через n и p. Выделим около дна зоны проводимости узкий интервал энергий dЕ, заключенный между Е и Е+dЕ. Так как электронный газ в полупроводнике является невырожденным, то число электронов dn, заполняющих интервал энергии dЕ (в расчете на единицу объема полупроводника), можно определить, воспользовавшись формулой :
. Так как для невырожденного газа уровень Ферми m должен располагаться ниже этого уровня, т.е. в запрещенной зоне, то m является величиной отрицательной (-m >>kT). При температуре Т, отличной от абсолютного нуля, в зоне проводимости находятся электроны, в валентной зоне – дырки. Обозначим их концентрацию соответственно через n и p. Выделим около дна зоны проводимости узкий интервал энергий dЕ, заключенный между Е и Е+dЕ. Так как электронный газ в полупроводнике является невырожденным, то число электронов dn, заполняющих интервал энергии dЕ (в расчете на единицу объема полупроводника), можно определить, воспользовавшись формулой :
N(E)dE=![]() (2m)
(2m)![]() e
e![]() E
E![]() dE
dE
dn=![]() (2m
(2m![]() )
)![]() e
e![]() e
e![]() E
E![]() dE
dE
где m – эффективная масса электронов, располагающихся у дна зоны проводимости.
Обозначим расстояние от дна зоны проводимости до уровня Ферми через -m, а от уровня Ферми до потолка валентной зоны через -m¢. Из рис. 1 видно, что
m+m¢=-E![]() ,
,
m¢=-(Е![]() +m)
+m)
где Е![]() (
(![]() Е) - ширина запрещенной зоны.
Е) - ширина запрещенной зоны.
E![]() =Е +bТ
=Е +bТ
Полное число электронов n, находящихся при температуре Т в зоне проводимости, получим, интегрируя (1.2) по всем энергиям зоны проводимости, т.е. в пределах от 0 до Е![]() :
:
n=4![]()
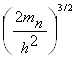
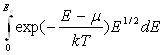
Так как с ростом Е функция exp(-E/kT) спадает очень быстро, то верхний предел можно заменить на бесконечность:
n=4![]()

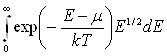
Вычисление этого интеграла приводит к следующему результату:
n=2 exp
exp ![]() (1.5)
(1.5)
N![]() =2(2
=2(2![]() m
m![]() kT/h
kT/h![]() )
)![]() (1.6)
(1.6)
Тогда (1.5) примет следующий вид:
n=N![]() exp(
exp(![]() /kT) (1.7)
/kT) (1.7)
Множитель N![]() в (1.7) называют эффективным числом состояний в зоне проводимости, приведенным ко дну зоны. Смысл этого числа состоит в следующем. Если с дном зоны проводимости, для которой Е=0, совместить N
в (1.7) называют эффективным числом состояний в зоне проводимости, приведенным ко дну зоны. Смысл этого числа состоит в следующем. Если с дном зоны проводимости, для которой Е=0, совместить N![]() состояний, то, умножив это число на вероятность заполнения дна зоны, равную f
состояний, то, умножив это число на вероятность заполнения дна зоны, равную f![]() (0)=exp(
(0)=exp(![]() /kT), получим концентрацию электронов в этой зоне.
/kT), получим концентрацию электронов в этой зоне.
Подобный расчет, проведенный для дырок, возникающих в валентной зоне, приводит к выражению:
p=2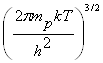 exp
exp![]() =N
=N![]() exp
exp![]() = N
= N![]() exp
exp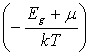 (1.8)
(1.8)
где
N![]() =2
=2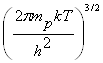 (1.9)
(1.9)
– эффективное число состояний в валентной зоне, приведенное к потолку зоны.
Из формул (1.7) и (1.8) следует, что концентрация свободных носителей заряда в данной зоне определяется расстоянием этой зоны от уровня Ферми: чем больше это расстояние, тем ниже концентрация носителей, так как m и m¢ отрицательны.
В собственных полупроводниках концентрация электронов в зоне проводимости n![]() равна концентрации дырок в валентной зоне p
равна концентрации дырок в валентной зоне p![]() , так как
, так как
каждый электрон, переходящий в зону проводимости, «оставляет» в валентной зоне после своего ухода дырку. Приравнивая правые части соотношения (1.5) и (1.8), находим
2 exp
exp ![]() =2
=2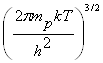 exp
exp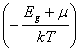
Решая это уравнение относительно m, получаем
m![]() = -
= -![]() +
+![]() kT ln
kT ln![]() (1.10)
(1.10)
Подставив m![]() из (1.10) в (1.5) и (1.7), получим
из (1.10) в (1.5) и (1.7), получим
n![]() =p
=p![]() =2
=2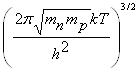 exp
exp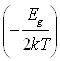 =(N
=(N![]() N
N![]() )
)![]() exp
exp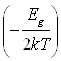 (1.11)
(1.11)
Из формулы (6.12) видно, что равновесная концентрация носителей заряда в собственном полупроводнике определяется шириной запрещенной зоны и температурой. Причем зависимость n![]() и p
и p![]() от этих параметров является очень резкой.
от этих параметров является очень резкой.
Рассчитаем собственную концентрацию электронов и дырок при Т=300К.
Eg=(0,782-3,9![]() 10
10![]()
![]() 300)1,6 10-19 =1,064
300)1,6 10-19 =1,064![]() 10-19 Дж
10-19 Дж
N![]() =2(2
=2(2![]() m
m![]() kT/h
kT/h![]() )
)![]() =2
=2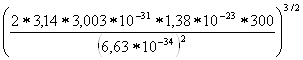 =2
=2![]() = =2
= =2![]() =4,7
=4,7![]() 10
10![]() (см
(см![]() )
)
N![]() =2
=2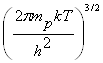 =2
=2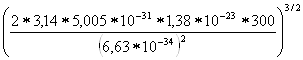 =2
=2![]() =10,2
=10,2![]() 10
10![]() (см
(см![]() )
)
n![]() =p
=p![]() =(N
=(N![]() N
N![]() )
)![]() exp
exp![]() =
=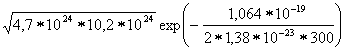 =
=
6,92![]() 10
10![]()
![]() 2
2![]() 10
10![]() =13,8
=13,8![]() 10
10![]() (см
(см![]() )
)
Похожие работы
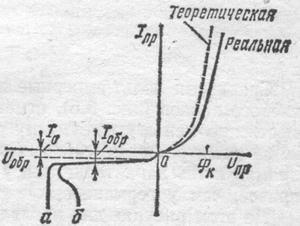
... облети присоединяют положительный полюс источника, p-n переход пропускают только малый ток неосновных носителей. Лишь при очень большом напряжении сила тока резко возрастает, что обусловлено электрическим пробоем перехода(обратное направление, левая ветвь ВАХ). При включении в цепь переменного тока p-n переходы действуют как выпрямители. Устройство в цепь пременного тока p-n переход, называется ...
... несколько сложнее, но, в любом случае наличие сборок предопределяет скачки. Практически в процессе естественной эволюции извержения на каждом ее этапе преобладает изменение лишь одного или двух параметров, и поведение системы может быть описано простой сборкой. Физический механизм катастрофического скачка заключается в следующем. Рост расхода приводит к росту скорости потока на всем протяжении ...
... его сопротивления и, таким образом, ток, протекающий через канал, порождает условия, при которых происходит ограничение его возрастания. Механизм насыщения скорости дрейфа позволяет получить совпадение теории и эксперимента; дело в том, что почти все падение напряжения сосредоточено в самой узкой части канала (верхней его части - горловине). В результате в этой области напряженность поля ...
... токи: , Наличие этих градиентов в p-n-переходе обуславливает существенное отличие его электрофизических свойств от свойств, прилегающих к нему p- и n-областей. Энергетическая диаграмма электронно-дырочного перехода. Энергетические диаграммы уединенных p- и n-областей полупроводника показаны на рисунке. В p-области уровень Ферми WFpсмещен в сторону валентной зоны, а в n-области уровень Ферми ...


0 комментариев