Навигация
Расчет контактной разности потенциалов
2. Расчет контактной разности потенциалов
Для n-области основными носителями являются электроны, для p-области – дырки. Основные носители возникают почти целиком вследствие ионизации донорных и акцепторных примесей. При не слишком низких температурах эти примеси ионизированы практически полностью, вследствие чего концентрацию электронов в n-области n![]() можно считать равной концентрации донорных атомов: n
можно считать равной концентрации донорных атомов: n![]() »N
»N![]() , а концентрацию дырок в p-области p
, а концентрацию дырок в p-области p![]() – концентрация акцепторных атомов в p-области: p
– концентрация акцепторных атомов в p-области: p![]() »N
»N![]() .
.
Помимо основных носителей эти области содержат не основные носители: n-область – дырки (p![]() ), p-область – электроны (n
), p-область – электроны (n![]() ). Их концентрацию можно определить, пользуясь законом действующих масс:
). Их концентрацию можно определить, пользуясь законом действующих масс:
n![]() p
p![]() = p
= p![]() n
n![]() =n
=n![]() .
.
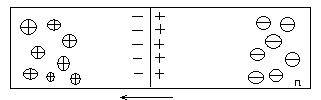
Как видим, концентрация дырок в p-области на 6 порядков выше концентрации их в n-области, точно так же концентрация электронов в n-области на 6 порядков выше их концентрации в p-области. Такое различие в концентрации однотипных носителей в контактирующих областях полупроводника приводит к возникновению диффузионных потоков электронов из n-области в p-область и дырок из p-области в n-область. При этом электроны, перешедшие из n- в p-область, рекомбинируют вблизи границы раздела этих областей с дырками p-области, точно так же дырки, перешедшие из p- в n-область, рекомбинируют здесьс электронами этой области. В результате этого в приконтактном слое n-области практически не остается свободных электронов и в нем формируется неподвижный объемный положительный заряд ионизированных доноров. В приконтактном слое p-области практически не остается дырок и в нем формируется неподвижный объемный отрицательный заряд ионизированных акцепторов.
Неподвижные объемные заряды создают в p–n-переходе контактное электрическое поле с разностью потенциалов V![]() , локализованное в области перехода и практически не выходящее за его пределы. Поэтому вне этого слоя, где поля нет, свободные носители заряда движутся по-прежнему хаотично и число носителей, ежесекундно наталкивающихся на слой объемного заряда, зависит только от их концентрации и скорости теплового движения. Как следует из кинетической теории газов, для частиц, подчиняющихся классической статистике Максвела–Больцмана, это число nопределяется следующим соотношением:
, локализованное в области перехода и практически не выходящее за его пределы. Поэтому вне этого слоя, где поля нет, свободные носители заряда движутся по-прежнему хаотично и число носителей, ежесекундно наталкивающихся на слой объемного заряда, зависит только от их концентрации и скорости теплового движения. Как следует из кинетической теории газов, для частиц, подчиняющихся классической статистике Максвела–Больцмана, это число nопределяется следующим соотношением:
n=![]() n
n![]() S, (2.1)
S, (2.1)
где n![]() - концентрация частиц;
- концентрация частиц;![]() - средняя скорость теплового движения; S – площадь, на которую они падают.
- средняя скорость теплового движения; S – площадь, на которую они падают.
Неосновные носители – электроны из p-области и дырки из n-области, попадая в слой объемного заряда, подхватываются контактным полем V![]() и переносятся через p–n-переход.
и переносятся через p–n-переход.
Обозначим поток электронов, переходящих из p- в n-область, через n![]() , поток дырок, переходящих из n- в p-область, через p
, поток дырок, переходящих из n- в p-область, через p![]() .
.
n![]() =
=![]() n
n![]()
![]()
![]() S, (2.2)
S, (2.2)
p![]() =
=![]() p
p![]()
![]()
![]() S. (2.3)
S. (2.3)
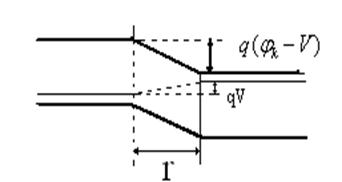
Иные условия складываются для основных носителей. При переходе из одной области в другую они должны преодолевать потенциальный барьер высотой qV![]() , сформировавшийся в p–n-переходе. Для этого они должны обладать кинетической энергией движения вдоль оси c, не меньшей qV
, сформировавшийся в p–n-переходе. Для этого они должны обладать кинетической энергией движения вдоль оси c, не меньшей qV![]() . Согласно (2.1) к p–n-переходу подходят следующие потоки основных носителей:
. Согласно (2.1) к p–n-переходу подходят следующие потоки основных носителей:
n![]() =
=![]() n
n![]()
![]()
![]() S,
S,
p![]() =
=![]() p
p![]()
![]()
![]() S.
S.
В соответствии с законом Больцмана преодолеть потенциальный барьер qV![]() сможет только n
сможет только n![]() exp (-qV
exp (-qV![]() /kT) электронов и p
/kT) электронов и p![]() exp (-qV
exp (-qV![]() /kT) дырок. Поэтому потоки основных носителей, проходящие через p–n-переход, равны
/kT) дырок. Поэтому потоки основных носителей, проходящие через p–n-переход, равны
n![]() =
=![]() n
n![]()
![]()
![]() exp (-qV
exp (-qV![]() /kT), (2.4)
/kT), (2.4)
p![]() =
=![]() p
p![]()
![]()
![]() exp (-qV
exp (-qV![]() /kT), (2.5)
/kT), (2.5)
На первых порах после мысленного приведения n- и p-областей в контакт потоки основных носителей значительно превосходят потоки неосновных носителей: n![]() >>n
>>n![]() , p
, p![]() >>p
>>p![]() . Но по мере роста объемного заряда увеличивается потенциальный барьер p–n-перехода qV
. Но по мере роста объемного заряда увеличивается потенциальный барьер p–n-перехода qV![]() и потоки основных носителей согласно (2.4) и (2.5) резко уменьшаются. В то же время потоки неосновных носителей, не зависящие от qV
и потоки основных носителей согласно (2.4) и (2.5) резко уменьшаются. В то же время потоки неосновных носителей, не зависящие от qV![]() [ см. (2.2) и (2.3)] остаются неизменными. Поэтому относительно быстро потенциальный барьер достигает такой высоты j
[ см. (2.2) и (2.3)] остаются неизменными. Поэтому относительно быстро потенциальный барьер достигает такой высоты j![]() = qV
= qV![]() , при которой потоки основных носителей сравниваются с потоками неосновных носителей:
, при которой потоки основных носителей сравниваются с потоками неосновных носителей:
n![]() =n
=n![]() , (2.6)
, (2.6)
p![]() =p
=p![]() . (2.7)
. (2.7)
Это соответствует установлению в p–n-переходе состояния динамического равновесия.
Подставляя в (2.6) n![]() из (2.4) и n
из (2.4) и n![]() из (2.2), а в (2.7) p
из (2.2), а в (2.7) p![]() из (2.5) и p
из (2.5) и p![]() из (2.3), получаем
из (2.3), получаем
n![]() exp (-qV
exp (-qV![]() /kT)= n
/kT)= n![]() , (2.8)
, (2.8)
p![]() exp (-qV
exp (-qV![]() /kT)= p
/kT)= p![]() . (2.9)
. (2.9)
Отсюда легко определить равновесный потенциальный барьер p–n-перехода j![]() = qV
= qV![]() . Из (2.8) находим
. Из (2.8) находим
j![]() = qV
= qV![]() = kTln (n
= kTln (n![]() / n
/ n![]() )= kTln (n
)= kTln (n![]() p
p![]() /n
/n![]() ). (2.10)
). (2.10)
j![]() = kTln (p
= kTln (p![]() / p
/ p![]() )=kTln (p
)=kTln (p![]() n
n![]() / n
/ n![]() ). (2.11)
). (2.11)
Из (2.10) и (2.11) следует, что выравнивание встречных потоков электронов и дырок происходит при одной и той же высоте потенциального барьера j![]() . Этот барьер тем выше, чем больше различие в концентрации носителей одного знака в n- и p-областях полупроводника.
. Этот барьер тем выше, чем больше различие в концентрации носителей одного знака в n- и p-областях полупроводника.
Рассчитаем контактную разность потенциалов при 300 К.
n![]() =N
=N![]() =1,0
=1,0![]() 10
10![]()
p![]() =N
=N![]() =1,0
=1,0![]() 10
10![]()
j![]() = kTln(p
= kTln(p![]() n
n![]() /n
/n![]() )=1,38
)=1,38![]() 10
10![]()
![]() 300
300![]() ln
ln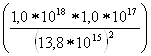 =
=
= 414![]() 10
10![]()
![]() 6,26=2,6
6,26=2,6![]() 10
10![]() (Дж)
(Дж)
V![]() =
=![]() =
=![]() =0,16 (В)
=0,16 (В)
Похожие работы
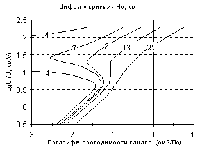
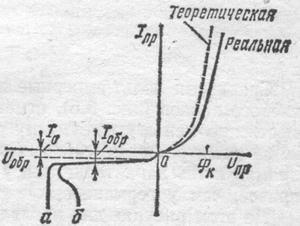
... облети присоединяют положительный полюс источника, p-n переход пропускают только малый ток неосновных носителей. Лишь при очень большом напряжении сила тока резко возрастает, что обусловлено электрическим пробоем перехода(обратное направление, левая ветвь ВАХ). При включении в цепь переменного тока p-n переходы действуют как выпрямители. Устройство в цепь пременного тока p-n переход, называется ...
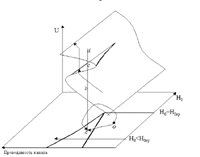
... несколько сложнее, но, в любом случае наличие сборок предопределяет скачки. Практически в процессе естественной эволюции извержения на каждом ее этапе преобладает изменение лишь одного или двух параметров, и поведение системы может быть описано простой сборкой. Физический механизм катастрофического скачка заключается в следующем. Рост расхода приводит к росту скорости потока на всем протяжении ...
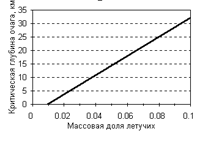
... его сопротивления и, таким образом, ток, протекающий через канал, порождает условия, при которых происходит ограничение его возрастания. Механизм насыщения скорости дрейфа позволяет получить совпадение теории и эксперимента; дело в том, что почти все падение напряжения сосредоточено в самой узкой части канала (верхней его части - горловине). В результате в этой области напряженность поля ...
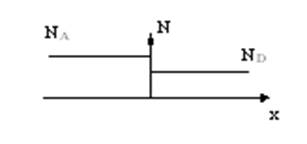
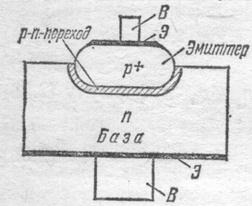
... токи: , Наличие этих градиентов в p-n-переходе обуславливает существенное отличие его электрофизических свойств от свойств, прилегающих к нему p- и n-областей. Энергетическая диаграмма электронно-дырочного перехода. Энергетические диаграммы уединенных p- и n-областей полупроводника показаны на рисунке. В p-области уровень Ферми WFpсмещен в сторону валентной зоны, а в n-области уровень Ферми ...


0 комментариев