Постановка задачі

Коефіцієнт швидкої ліквідності Постановка задачі Методика розрахунку точності прогнозування за критерієм Персона Ефективність отриманих результатів Робочі місця, що уперше вводяться в експлуатацію після запровадження в дію цих Правил, повинні в повному обсязі задовольняти їхньої вимоги Підходи до засобів пожежегасіння повинні бути вільними

86676

знаков

таблиц

изображение

Коефіцієнт швидкої ліквідності Читать далее: Методика розрахунку точності прогнозування за критерієм Персона

1.6 Постановка задачі

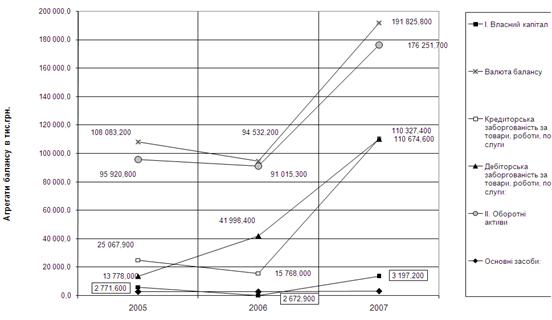
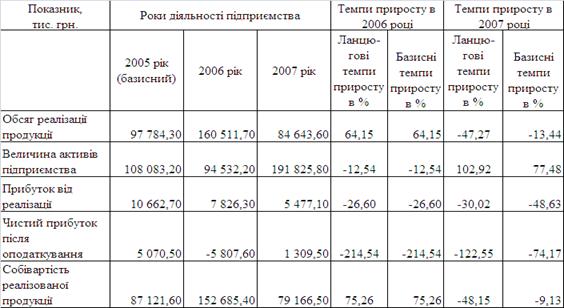
Після того, як завод отримав статус відкритого акціонерного товариства, з`явились певні проблеми та складнощі. Завод з ремонту та будівництву пасажирських вагонів, після того як отримав статус відкритого акціонерного товариства, та в результаті чого з`явилися акціонери які мають надію отримати для себе певну вигоду. Відомо, що державні настанови далеко не зовсім співпадають з інтересами підприємців та акціонерів, бо у останніх мета отримати якомога більший прибуток. А для отримання максимального прибутку треба налагодити економічну діяльність підприємства, що є мабуть однією з найважливіших сторін підприємства. Якщо є питання з приводу того, що саме треба зробити для чіткої та організованої економічної моделі? То за відповіддю далеко йти не потрібно. Одним з методів поліпшення економіки є прогнозування зміни економічних показників у часі. Для цього беруться певні фінансові коефіцієнти по яким будується схема прогнозу. А саме нам потрібні наступні коефіцієнти:

- коефіцієнт зміни валового прибутку.

- коефіцієнт зміни прибутку до виплати відсотків і податків.

- коефіцієнт зміни аналізу операційних витрат.

- коефіцієнт зміни керуванням активами.

- коефіцієнт зміни оборотності постійних активів.

- коефіцієнт зміни оборотності запасів.

- коефіцієнт зміни ліквідності.

- коефіцієнт зміни поточної ліквідності.

- коефіцієнт зміни фінансового левериджу.

- коефіцієнт зміни довгострокової заборгованості.

- коефіцієнт зміни середнього періоду погашення дебіторської заборгованості.

Оскільки характер зміни цих вибраних коефіцієнтів нелінійних, потрібно застосовувати новітні методи отримання числових значень коефіцієнтів у формулах апроксимації.

2 ТЕОРЕТИЧНА ЧАСТИНА

2.1 Опис методики отримання формул апроксимації довільного вигляду

Економічні цикли, сезонність продаж, цикл життя товару або послуги та інші чинники можуть суттєво впливати на економічні показники окремого підприємства. Періодичність економічних процесів викликана зміною життєвої активності людей протягом доби, тижня, місяця та року (існують і більші періоди циклічності).

Тому перед дослідниками постає задача підбору такого виду функції, яка б своєю формою відповідала основним формам періодичних і неперіодичних залежностей економічних процесів. Другою задачею є визначення коефіцієнтів обраної функції за вибіркою статистичних даних.

Існуючі в економіці залежності повинні мати не тільки періодичні функції, але й експоненціальні та степеневі. Тому була обрана наступна формула

, (2.1.1)

де х – аргумент, у – функція, A - Н – константи, e – основа натурального логарифму. В залежності від чисельних значень констант, ця формула дає множину кривих, представлену на рис.2.1.1.

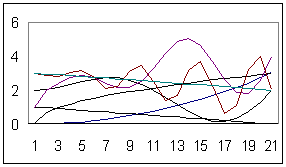
Рис. 2.1.1 Типи кривих, які можна створити за допомогою формули (2.1.1)

Вирішення другої задачі ускладнюється тим, що не існує таких математичних перетворень, які б дозволили лінеаризувати (2.1.1), щоб потім отримати значення констант A - Н методом регресії або найменших квадратів. Тому був застосований наступний оптимізаційний підхід:

1. Встановити довільні значення констант A - Н .

2. Для всіх значень аргументу і довільних значень констант розрахувати величину у, яку позначимо як у_р за формулою.

3. Для кожного значення функції знайти (у_р – у_ф)², де у_ф – фактичне значення функції, отримане за статистичними даними.

4. Вирішити оптимальну задачу з функціоналом виду

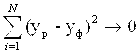, (2.1.2)

а параметрами, що змінюються, будуть константи A - Н . Де N – розмір статистичної вибірки.

Вже перші розрахунки за допомогою функції “Пошук рішень” електрон-них таблиць Excel показали, що константи E та G визначаються як нулі у випадку, коли амплітуда синусоїди менше середнього значення функції у 3-10 разів. Тому, для збільшення точності розрахунку, рекомендується встановлювати обмеження на значення констант за наступним правилом:

1. На графіку, який було побудовано за статистичними даними, виділяється елемент кривої, що нагадує синусоїду і знаходиться проміжок значень аргументу, на якому ця синусоїда здійснює повне коливання – Δх. Тоді, для константи E треба встановити наступне обмеження

E ≤ (0,5 – 1,5) 2π/Δх₁. (2.1.3)

2. Початкові значення констант B та F рекомендується становити рівними одиниці, константи Н – середньому арифметичному статистичного значення функції, константу – D - 0.05, А=0.

3. Константа C визначається з максимальної амплітуди Δу тієї частини графіку, яка визначена як синусоїдальна, і має наступні обмеження

С ≤ (0,4 – 0,6) Δу. (2.1.4)

Наведемо приклади застосування запропонованої методики. Нижче під заголовками наведені графіки різних періодичних процесів економіка, а в таблиці 2.1.1. подані значення констант для цих графіків, знайдені з урахуванням. В малюнках прийняті наступні умовні позначення у_р – ■ у_ф – ♦.

Таблиця 2.1.1.

Номер рисунка	Значення констант для (1)
Номер рисунка	A	B	C	D	E	F	G	H
2	0,00145	7,34660	150000	-29,39	0,9	-0,436	-0,39	98923
3	11042,3	-3,901	25396,8	-0,899	0,855	0,8772	0,409	226049
4	-22,22	0,7731	4204,4	-0,009	0,0006	4,5492	7,829	285,39
5	595,51	-4,862	60	0,0235	1	0,8697	9,5	45
6	17,0537	0,57627	19,9770	-0,05	201,32	-94,12	1,684	30,100

Споживання палива енергогенеруючою компанією

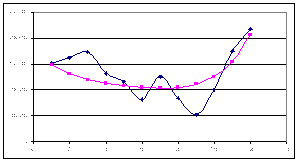
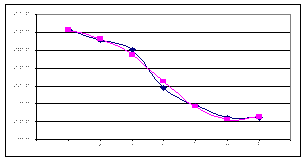
Рис. 2.1.2. За місяцями Рис. 2.1.3. За днями тижня

Потік замовлень на підприємство зв’язку

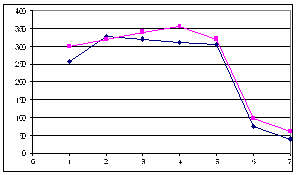
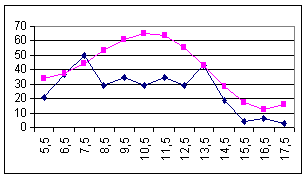
Рис. 2.1.4. За днями тижня Рис. 2.1.5. За годинами робочого дня

Залежність прибутку приватного підприємства від свого попереднього значення.

В цьому випадку була використана так звана авторегресійна модель, тобто залежність прибутків та збитків (прибутків зі знаком мінус) від своїх попередніх значень. Оскільки формула не дає бажаного результату, якщо якесь число зі статистичної вибірки має від’ємне значення (константи B та F можуть бути дробовими, а, отже, жодне значення аргументу не може бути від’ємним, бо воно знаходиться через логарифмування), то до значень статистичної вибірки було додано число більше за найбільше за модулем від’ємне значення аргументу.

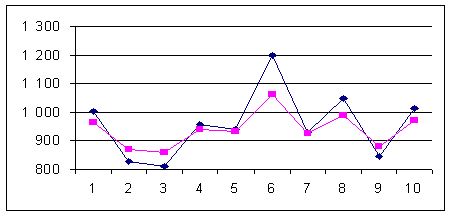
Рис.2.1.6 Прибуток за кварталами

З отриманих результатів проведених досліджень можна зробити наступні висновки:

1. Запропонований оптимізаційний алгоритм дозволяє будувати модель циклічних економічних процесів за будь-якою наперед обраною формулою.

2. Запропонована формула дозволяє будувати моделі різних за своєю природою економічних процесів.

2.2 Опис методики отримання числових коефіцієнтів за допомогою метода Ньютона

Метод Ньютона може бути віднесено до оптимізаційних задач в наступній постановці

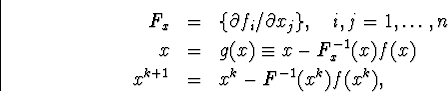$\begin{eqnarray}F_x&=&\{\partial f_i/\partial x_j\},\quad i,j=1,\ldots,n\nonum... ...quiv x-F^{-1}_x(x)f(x)\nonumber\\ x^{k+1}&=&x^k-F^{-1}(x^k)f(x^k),\end{eqnarray}$ (2.2.1)

тобто потрібно вирішити систему F_x(x^k⁺¹-x^k)=-f(x^k) . Будемо використовувати $x,\enskipf,\enskip g$ - розуміючи під цим вектора.

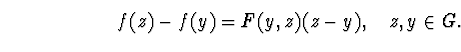
$\begin{equation}f(z)-f(y)=F(y,z)(z-y),\quad z,y\in G.\end{equation}$

Теорема 3. Якщо f_i(x) безперервні, разом з першими похідними в опуклій області G , що містить рішення системи $X^{\ast}$ і при $x= X^{\ast}$ матриця F_x не вироджена, то існує така околиця $R \{\Vert x-X^{\ast}\Vert,<\delta\}$ що при кожнім $x^0\in R$ метод Ньютона сходиться к. $x^{\ast}$ $\Box$

Доказ. Розглянемо

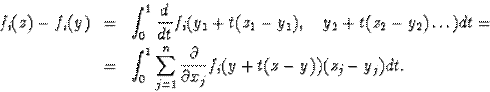$\begin{eqnarray*}f_i(z)-f_i(y)&=&\int^1_0\frac{d}{dt}f_i(y_1+t(z_1-y_1),\quady... ...um^n_{j=1}\frac{\partial}{\partial x_j}f_i(y+t(z-y))(z_j-y_j)dt.\end{eqnarray*}$ (2.2.2)

Введемо

$F_{ij}(y,z)=\int^1_0\frac{\partial}{\partial x_j}f_i(y+t(z-y))dt$

і матрицю

$F(y,z)=\{F_{ij}\}$ .

Очевидно, що F(x,x)= F(x) , тобто маємо тотожності

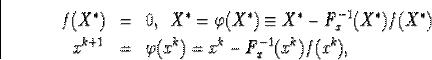$\begin{eqnarray*}f(X^{\ast})&=&0,\enskip X^{\ast}=\varphi(X^{\ast})\equiv X^{\... ...st})f(X^{\ast})\\ x^{k+1}&=&\varphi(x^k)=x^k-F^{-1}_x(x^k)f(x^k),\end{eqnarray*}$ (2.2.3)

тоді

$x^{k+1}-X^{\ast}=x^k-X^{\ast}-F^{-1}_x(x^k)(f(x^k)-f(X^{\ast}))$

Використовуючи одержимо

$\begin{displaymath}x^{k+1}-X^{\ast}=\big[E-F^{-1}_x(x^k)F(X^{\ast},x^k)\big](x^k-X^{\ast}).\end{displaymath}$

Поблизу околиці $X^{\ast}$ для кожного $\delta\gt$ найдеться таке x⁰ , що якщо

$\Vert x^0-X^{\ast}\Vert<\delta$ ,

то $\begin{displaymath}\Vert E-F^{-1}_x(x^0)F(X^{\ast},x^0)\Vert\leq K<1.\end{displaymath}$

Тоді $\begin{displaymath}\vert x^1-X^{\ast}\Vert\leq K\cdot\delta<\delta,\end{displaymath}$

тобто

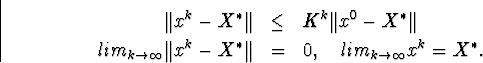
$\begin{eqnarray*}\Vert x^k-X^{\ast}\Vert& \leq &K^k\Vert x^0-X^{\ast}\Vert\\ li... ...}\Vert x^k-X^{\ast}\Vert&=&0,\quad lim_{k\to\infty}x^k=X^{\ast}.\end{eqnarray*}$

На початкове наближення x⁰ накладена умова, яку перевірити складно.

Теорема Канторовича 4. Якщо функції f_i(x) безперервні разом зі своїми 1 -ми і 2 -ми похідними в деякій опуклій області G , що містить крапку x⁰ разом з її околицею $\{\Vert x-x^0\Vert\leq\rho\}$ і виконані наступні умови:

1) у крапці x⁰ існує матриця F^-1 така

$\begin{displaymath}\Vert F^{-1}_x(x^0)\Vert _{\infty}\leq M_0\end{displaymath}$

2) $\Vert f(x^0)\Vert _{\infty}\leq\delta;\quad M_0\delta=r_0\leq\rho/2$ (2.2.4)

3) $\sum^n_{k=1}\arrowvert\frac{\partial^2f_i(x)}{\partial x_j\partial x_k}\arrowvert\leq N,\quad i,j=1,\ldots,n;\quad x\in R;$ (2.2.5)

4) $h_0=2nr_0M_0N\leq 1,$ (2.2.6)

те послідовність x^k⁺¹=x^k-f^-1_x(x^k)F(x^k) сходиться к. $X^{\ast}$ $X^{\ast}$ є єдиним рішенням системи f(x)=0 в області $\Vert x-x^0\Vert\leq 2r_0$ і має місце оцінка

$\begin{displaymath}\Vert X^{\ast}-x^k\Vert _1\leq(\frac{1}{2})^{k-1}h^{2^k}_0r_0.\end{displaymath}$ $\Box$

Доведемо 3 нерівності

а) $\Vert f(x+\Delta x)-f(x)\Vert _{\infty}\leq F_x(\xi)\Vert\Vert\Delta x\Vert$

б) $\Vert F_x(x+\Delta x)-F_x(x)\Vert\leq nN\Vert\Delta x\Vert$

в) $\Vert f(x+\Delta x)-f(x)-F_x(x)\Delta x\Vert\leq\frac{1}{2}nN\Vert\Delta x\Vert^2_{\infty}$

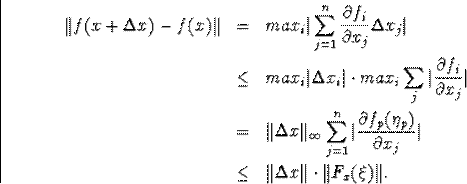
а) $\begin{eqnarray*}\Vert f(x+\Deltax)-f(x)\Vert&=&max_i\vert\sum^n_{j=1} \frac{\... ...ial x_j}\vert\\ &\leq&\Vert\Deltax\Vert\cdot\Vert F_x(\xi)\Vert.\end{eqnarray*}$

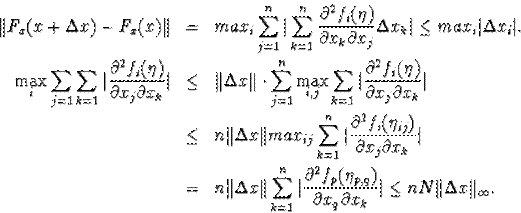
б) $\begin{eqnarray*}\Vert F_x(x+\Deltax)-F_x(x)\Vert&=&max_i\sum^n_{j=1}\vert\sum... ...partial x_q\partial x_k}\vert\leq nN\Vert\Deltax\Vert _{\infty}.\end{eqnarray*}$

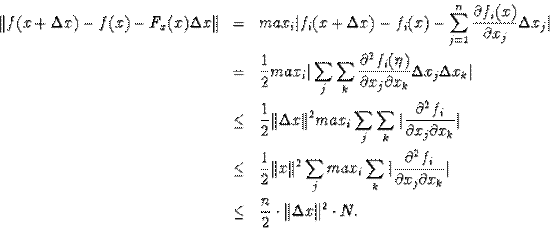
в) $\begin{eqnarray*}\Vert f(x+\Delta x)-f(x)-F_x(x)\Delta x\Vert&=&max_i\vert f_i... ...al x_k}\vert\\ &\leq&\frac{n}{2}\cdot\Vert\Delta x\Vert^2\cdot N.\end{eqnarray*}$

З ітераційного процесу при k=0

$\begin{displaymath}\Vert x^1-x^0\Vert=\Vert F^{-1}_x(x^0)f(x^0)\Vert\leq\Vert F^{-1}_x\Vert\Vert f(x^0)\Vert\leqM_0\delta=r_0<\frac{\rho}{2}.\end{displaymath}$

Тепер

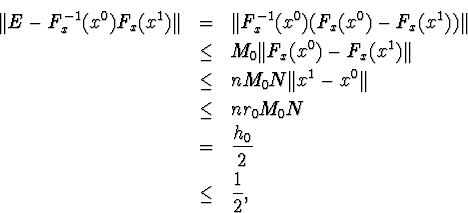
$\begin{eqnarray*}\Vert E-F^{-1}_x(x^0)F_x(x^1)\Vert&=&\Vert F^{-1}_x(x^0)(F_x(x... ...0\Vert\\ &\leq&nr_0M_0N\\ &=& \frac{h_0}{2}\\ &\leq&\frac{1}{2},\end{eqnarray*}$

тобто матриця F^-1_x(x⁰)F_x(x¹) не вироджена, і

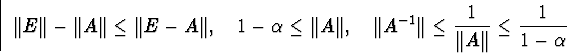
$\begin{displaymath}\Vert\big[F^{-1}_x(x^0)F_x(x^1)\big]^{-1}\Vert\leq\frac{1}{1-h_0/2}\leq 2.\end{displaymath}$ $\begin{displaymath}\Vert E\Vert-\Vert A\Vert\leq\Vert E-A\Vert,\quad1-\alpha\l... ...rt A^{-1}\Vert\leq\frac{1}{\Vert A\Vert}\leq\frac{1}{1-\alpha}\end{displaymath}$ $\begin{displaymath}F^{-1}_x(x^1)=\big[F^{-1}_x(x^0)F_x(x^1)\big]^{-1}F^{-1}_x(x^0)\end{displaymath}$ і $\begin{displaymath}\Vert F^{-1}_x(x^1)\Vert\leq 2\cdot M_0.\end{displaymath}$

З F_x(x⁰)(x¹-x⁰)+f(x⁰)=0

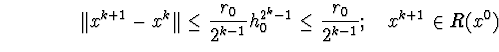
$\begin{equation}\Vert x^{k+1}-x^k\Vert\leq\frac{r_0}{2^{k-1}}h^{2^k-1}_0\leq\frac{r_0}{2^{k-1}};\quad x^{k+1}\in R(x^0)\end{equation}$ $\begin{displaymath}\Vert f(x^1)\Vert\leq\Vert f(x^1)f(x^0)-F_x(x_0)(x^1-x^0)\Vert\leq\frac{1}{2}nN\cdot r^2_0\end{displaymath}$ $\begin{displaymath}\Vert F^{-1}(x^1)f(x^1)\Vert\leq\frac{1}{2} nN\cdotr^2_0\cdot 2M_0=(M_0nr_0N)r_0=\frac{h_0r_0}{2}\leq\frac{r_0}{2}.\end{displaymath}$

Покажемо, що при всіх k мають місце нерівності:

$\begin{displaymath}\Vert F^{-1}_x(x^k)\Vert\leq 2M_0;\quad \Vert f(x^k)\Vert\leq\frac{nNr^2_0}{2^{2k-1}}h^{2^k-2}_0\leq\frac{nNr^2_0}{2^{2k-1}}.\end{displaymath}$ (2.2.6)

$\begin{displaymath}\Vert F^{-1}_x(x^k)f(x^k)\Vert\leq\frac{r_0}{2^k} \mbox{, при }k=1\mbox{ ужепоказали.}\end{displaymath}$

Нехай має місце m=k-1 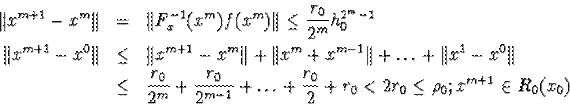$\begin{eqnarray*}\Vert x^{m+1}-x^m\Vert&=&\Vert F^{-1}_x(x^m)f(x^m)\Vert\leq\fr... ...1}}+\ldots+\frac{r_0}{2}+r_0<2r_0\leq\rho_0; x^{m+1}\in R_0(x_0)\end{eqnarray*}$

Повторимо нерівності

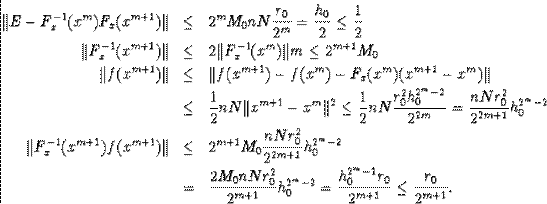
$\begin{eqnarray*}\Vert E-F^{-1}_x(x^m)F_x(x^{m+1})\Vert&\leq& 2^mM_0nN\frac{r_0... ...{2^m-2}_0=\frac{h^{2^m-1}_0r_0}{2^{m+1}}\leq\frac{r_0}{2^{m+1}}.\end{eqnarray*}$

Нерівність показує, що в колі R послідовність x^k є фундаментальною, тобто мається межа.

Оцінимо збіжність

$\begin{eqnarray*}\Vert x^{k+p}-x^k\Vert&\leq&\Vert x^{k+p}-x^{k+p-1}\Vert+\ldot... ...\ldots+\frac{1}{2^{p-1}}\big]\leq\frac{r_0}{2^{k-1}}h^{2^k-1}_0,\end{eqnarray*}$

тобто, спрямовуючи $p\to\infty$ права частина не міняється, $\Vert X^{\ast}-x^k\Vert\leq\frac{r_0}{2^{k-1}}h^{2^k-1}_0$ , тобто при дуже гарна збіжність.

Модифікація методу Ньютона в тім, що F^-1_x(x^kp) обчислюють не на кожнім кроці; при $k_p\leq k<k_{p+1}$ матриця не міняється, що різко зменшує число арифметичних дій, але накладає більш тверді обмеження на область і швидкість збіжності.

Раздел: Экономико-математическое моделирование
Количество знаков с пробелами: 86676
Количество таблиц: 19
Количество изображений: 41

Скачать

... ійного підвищення цін над зростанням її фізичного обсягу свідчить про підвищення попиту на неї); 2) відношення прибутку від реалізації продукції на зовнішньому ринку до обсягу її експорту (збільшення такого показника вказує на підвищення конкурентоспроможності продукції); 3) відношення обсягів реалізації експортної продукції до вартості матеріально-виробничих запасів (зменшення цього показника ...

Скачать

... яльність щодо зберігання зерна, міститься інформація про обсяги і рух зерна протягом місяця. Наступним заходом для створення організаційних умов конкурентоспроможного виробництва, формування рівноважного ринку зерна та налагодження діяльності зернопродуктового підкомплексу повинно відбутися врегулювання цін на зерно в післяжнивний період, що характеризується найбільшою диспропорційністю між міні ...

Скачать

... підприємства - це покупка фірмою ТОВ «Граніт» у ВАТ “Запорізьке кар’єроуправління” в 2007 році гранітного кар'єру «Дніпропетровський-1» та початок ведення відбудовних робіт на його території. . Основне фінансування здійснюється за рахунок Статутного капіталу підприємства. Другорядним джерелом фінансування - є кредитування під заставу кар'єрної техніки. У перспективі, планується збувати продукц ...

Скачать

... парка обладнання підприємства. Всі ці задачі розглядаються більш конкретно в наступному підрозділі роботи. 1.3 Проблеми законодавчого регулювання і стимулювання відновлення устаткування, як методу підвищення ефективності виробництва Науково-практичні завдання, що потребують рішення у процесі відновлення ОВФ в Україні, витікають з цілої низки взаємозалежних проблем, що виникають на усіх рівнях ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями