Коефіцієнт швидкої ліквідності
Постановка задачі
Методика розрахунку точності прогнозування за критерієм Персона
Ефективність отриманих результатів
Робочі місця, що уперше вводяться в експлуатацію після запровадження в дію цих Правил, повинні в повному обсязі задовольняти їхньої вимоги
Підходи до засобів пожежегасіння повинні бути вільними
Навигация
Методика розрахунку точності прогнозування за критерієм Персона
Прогнозування зміни економічних показників у часі ВАТ "Вагоно-ремонтний завод"
86676
знаков
19
таблиц
41
изображение
2.3 Методика розрахунку точності прогнозування за критерієм Персона
Для визначення точності прогнозування необхідно знайти різницю між прогнозованим і реальним значенням параметра.
Нуль-гіпотеза приймається, якщо критерій узгодження Пірсона (або «хі-квадрат»)
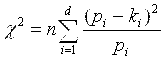, (2.3.1)
буде менший або дорівнювати табличному значенню цього критерію при достатньо великому значенні довірчої ймовірності. Фрагмент таблиці критерію Пірсона χ2(r, р) поданий нижче. Тут п – розмір вибірки, kі – прогнозоване значення параметру; рі – реальне значення параметру: d – загальна кількість діапазонів, на які розбита область існування випадкової величини. r= d - 1 – число ступенів свободи.
Таблиця 2.3.1. Значення χ2(r, р)| r р | 1 | 3 | 5 | 7 | 10 | 15 | 20 | 25 | 30 |
| 0,99 | 0 | 0,115 | 0,554 | 1,239 | 2,56 | 5,23 | 8,26 | 11,52 | 14,95 |
| 0,95 | 0,004 | 0,352 | 1,145 | 2,17 | 3,94 | 7,26 | 10,85 | 14,61 | 18,49 |
| 0,9 | 0,016 | 0,584 | 1,61 | 2,83 | 4,86 | 8,55 | 12,44 | 16,47 | 20,6 |
| 0,8 | 0,064 | 1,005 | 2,34 | 3,82 | 6,18 | 10,31 | 14,58 | 18,94 | 23,4 |
2.4 Результати отримання числових значень коефіцієнтів у апроксимаційних формулах
Для цього було взято перші 12 точок значень кожного числового коефіцієнта і виконано розрахунок коефіцієнтів в апроксимаційних формулах у наступному порядку:
1. Проведена лінія тренду по реальним значенням параметру К з визначенням формули лінії тренду Y(x). Тут і далі х – номер часового періоду, з кроком в один квартал, починаючи з 1-го кварталу 2004 року.
2. Різниця між лінією тренду і реальними значеннями була апроксимована за наведеною вище методикою Y(x)-K.
3. Для різниці було застосовано методику нелінійної апроксимації і отримано числові значення коефіцієнтів складної формули y(x).
4. Три останніх точки були використані для перевірки за критерієм Пірсона якості прогнозування із застосуванням функції ХИ2РАСП електронних таблиць Excel. Було визначено рівень довірчої ймовірності при заданому рівні хі-квадрат та числа степенів свободи.
Результати розрахунків представлено на рис. 4.4.1-2.4.22 і в табл.. 2.4.1.-2.4.11.
Значення довірчої імовірності якості прогнозування зведені в табл.. 2.4.12.
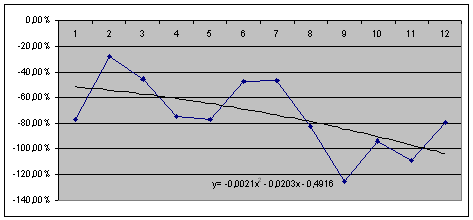
Рис. 2.4.1. Графік зміни коефіцієнта валового прибутку(
) та лінії тренда (
) з формулою.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | -76,83% | -51,40% | -0,25 | -0,01 | 0,06 | -52,58% | -7,65% |
| 2 | -28,02% | -54,06% | 0,26 | 0,06 | 0,04 | -48,39% | -14,81% |
| 3 | -45,40% | -57,14% | 0,12 | 0,02 | 0,01 | -55,21% | -2,21% |
| 4 | -74,52% | -60,64% | -0,14 | -0,14 | 0 | -74,36% | 0,00% |
| 5 | -76,83% | -64,56% | -0,12 | 0 | 0,02 | -64,30% | -2,04% |
| 6 | -47,30% | -68,90% | 0,22 | 0,22 | 0 | -47,17% | 0,00% |
| 7 | -46,48% | -73,66% | 0,27 | 0,20 | 0 | -53,38% | -1,03% |
| 8 | -82,16% | -78,84% | -0,03 | -0,03 | 0 | -81,51% | -0,01% |
| 9 | -125,57% | -84,44% | -0,41 | -0,25 | 0,03 | -109,37% | -2,09% |
| 10 | -93,90% | -90,46% | -0,03 | -0,28 | 0,06 | -118,02% | -6,19% |
| 11 | -108,95% | -96,90% | -0,12 | -0,07 | 0 | -103,78% | -0,25% |
| 12 | -79,06% | -103,76% | 0,25 | 0,27 | 0 | -76,47% | -0,09% |
| 13 | -109,69% | -111,04% | 0,01 | 0,60 | 0,35 | -50,91% | 53,59% |
| 14 | -76,99% | -118,70% | 0,42 | 0,80 | 0,15 | -38,84% | 49,55% |
| 15 | -66,27% | -126,90% | 0,61 | 0,82 | 0,05 | -44,51% | 32,84% |
 |
(2.4.1)
Рис. 2.4.2. Графік зміни коефіцієнта валового прибутку () апроксимуючого графіка (
) та результатів перевірки якості прогнозування (після горизонтальної лінії (
)).
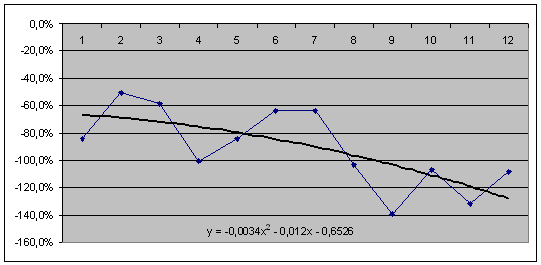
Рис. 2.4.3. Графік зміни коефіцієнта прибутку до виплати відсотків і податків () та лінії тренда () з формулою.
Таблиця 2.4.2. Результат розрахунку числових значень коефіцієнта прибутку до виплати відсотків і податків.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | -84,10% | -66,80% | -0,17 | -0,06 | 0,01 | -73,08% | -0,01 |
| 2 | -50,23% | -69,02% | 0,19 | 0,03 | 0,02 | -65,71% | -0,05 |
| 3 | -58,91% | -71,92% | 0,13 | 0,01 | 0,01 | -70,73% | -0,02 |
| 4 | -100,42% | -75,50% | -0,25 | -0,11 | 0,02 | -86,91% | -0,02 |
| 5 | -84,10% | -79,76% | -0,04 | 0,02 | 0 | -78,20% | 0,00 |
| 6 | -63,64% | -84,70% | 0,21 | 0,21 | 0 | -63,44% | 0,00 |
| 7 | -63,52% | -90,32% | 0,27 | 0,20 | 0 | -70,57% | -0,01 |
| 8 | -103,14% | -96,62% | -0,07 | -0,02 | 0 | -98,41% | 0,00 |
| 9 | -139,33% | -103,60% | -0,36 | -0,22 | 0,02 | -125,70% | -0,01 |
| 10 | -107,21% | -111,26% | 0,04 | -0,23 | 0,08 | -134,68% | -0,07 |
| 11 | -132,09% | -119,60% | -0,12 | -0,04 | 0,01 | -123,52% | -0,01 |
| 12 | -108,20% | -128,62% | 0,20 | -0,25 | 0 | -103,96% | 0,00 |
| 13 | -142,38% | -85,28% | -0,57 | 0,46 | 1,07 | -38,79% | 0,73 |
| 14 | -104,58% | -86,82% | -0,18 | 0,51 | 0,47 | -36,20% | 0,65 |
| 15 | -93,95% | -88,36% | -0,06 | 0,35 | 0,17 | -53,27% | 0,43 |
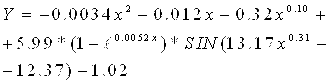(2.4.2)
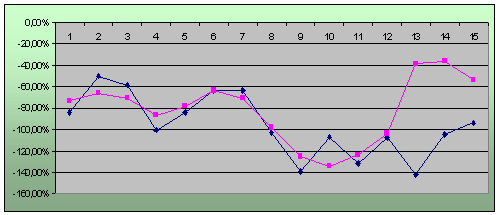
Рис. 2.4.4. Графік зміни коефіцієнта прибутку до виплати відсотків і податків () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
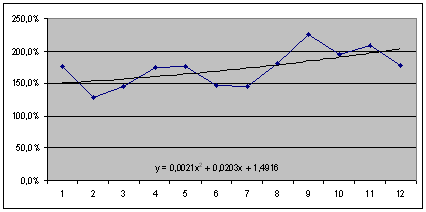
Рис. 2.4.5. Графік зміни коефіцієнта аналізу операційних витрат () та лінії тренда () з формулою.
Таблиця 2.4.3. Результат розрахунку числових значень коефіцієнта аналізу операційних витрат.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 176,83% | 151,40% | 0,25 | 0,01 | 0,06 | 152,05% | 0,03 |
| 2 | 128,02% | 154,06% | -0,26 | -0,08 | 0,03 | 146,37% | 0,03 |
| 3 | 145,40% | 157,14% | -0,12 | -0,06 | 0,00 | 151,15% | 0,00 |
| 4 | 174,52% | 160,64% | 0,14 | 0,10 | 0,00 | 170,90% | 0,00 |
| 5 | 176,83% | 164,56% | 0,12 | 0,04 | 0,01 | 168,51% | 0,00 |
| 6 | 147,30% | 168,90% | -0,22 | -0,18 | 0,00 | 150,43% | 0,00 |
| 7 | 146,48% | 173,66% | -0,27 | -0,21 | 0,00 | 153,20% | 0,00 |
| 8 | 182,16% | 178,84% | 0,03 | -0,06 | 0,01 | 184,42% | 0,00 |
| 9 | 225,57% | 184,44% | 0,41 | 0,31 | 0,01 | 215,81% | 0,00 |
| 10 | 193,90% | 190,46% | 0,03 | 0,28 | 0,06 | 218,81% | 0,03 |
| 11 | 208,95% | 196,90% | 0,12 | 0,00 | 0,01 | 196,47% | 0,01 |
| 12 | 179,06% | 203,76% | -0,25 | -0,25 | 0,00 | 178,54% | 0,00 |
| 13 | 209,69% | 211,04% | -0,01 | -0,18 | 0,03 | 193,15% | 0,08 |
| 14 | 176,99% | 218,74% | -0,42 | 0,25 | 0,45 | 243,51% | -0,38 |
| 15 | 166,27% | 226,86% | -0,61 | 0,80 | 1,98 | 307,12% | -0,85 |
(2.4.3)
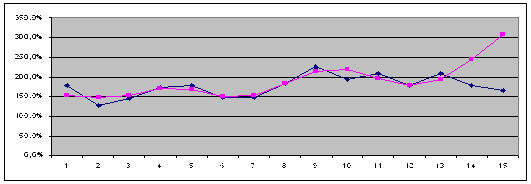
Рис. 2.4.6. Графік зміни коефіцієнта аналізу операційних витрат () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
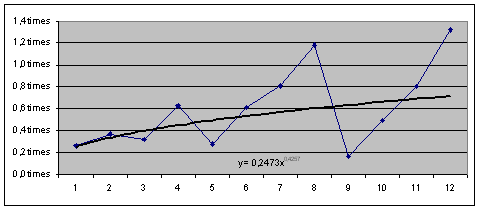
Рис. 2.4.7. Графік зміни коефіцієнта керуванням активами () та лінії тренда () з формулою.
Таблиця 2.4.4. Результат розрахунку числових значень коефіцієнта керуванням активами.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 0,3 | 0,2 | 0,01 | 0,01 | 0,00 | 0,26 | 0,00 |
| 2 | 0,4 | 0,3 | 0,03 | 0,06 | 0,00 | 0,39 | 0,00 |
| 3 | 0,3 | 0,4 | -0,08 | 0,02 | 0,01 | 0,42 | 0,03 |
| 4 | 0,6 | 0,4 | 0,18 | 0,23 | 0,00 | 0,68 | 0,00 |
| 5 | 0,3 | 0,5 | -0,22 | -0,12 | 0,01 | 0,37 | 0,03 |
| 6 | 0,6 | 0,5 | 0,09 | -0,07 | 0,02 | 0,46 | 0,04 |
| 7 | 0,8 | 0,6 | 0,24 | 0,36 | 0,01 | 0,93 | 0,02 |
| 8 | 1,2 | 0,6 | 0,58 | 0,26 | 0,10 | 0,86 | 0,09 |
| 9 | 0,2 | 0,6 | -0,46 | -0,26 | 0,04 | 0,37 | 0,26 |
| 10 | 0,5 | 0,7 | -0,17 | -0,35 | 0,03 | 0,31 | 0,06 |
| 11 | 0,8 | 0,7 | 0,12 | 0,16 | 0,00 | 0,85 | 0,00 |
| 12 | 1,3 | 0,7 | 0,61 | 0,62 | 0,00 | 1,34 | 0,00 |
| 13 | 0,4 | 0,7 | -0,38 | 0,46 | 0,71 | 1,20 | -2,36 |
| 14 | 0,6 | 0,8 | -0,16 | -0,17 | 0,00 | 0,59 | 0,02 |
| 15 | 0,7 | 0,8 | -0,10 | -0,65 | 0,31 | 0,13 | 0,81 |
(2.4.4)
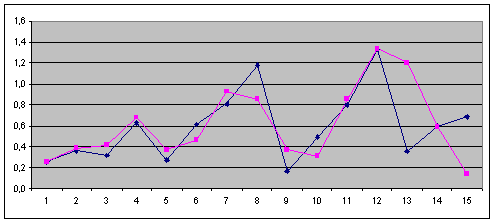
Рис. 2.4.8. Графік зміни коефіцієнта керуванням активами () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
Рис. 2.4.9. Графік зміни коефіцієнта оборотністю постійних активів () та лінії тренда () з формулою.
Таблиця 2.4.5. Результат розрахунку числових значень коефіцієнта оборотності постійних активів.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 0,54 | 0,45 | 0,08 | 0,09 | 0,00 | 0,54 | 0,00 |
| 2 | 0,74 | 0,77 | -0,03 | 0,20 | 0,05 | 0,97 | 0,07 |
| 3 | 0,70 | 1,04 | -0,35 | 0,09 | 0,19 | 1,13 | 0,27 |
| 4 | 2,05 | 1,30 | 0,76 | 1,06 | 0,09 | 2,36 | 0,05 |
| 5 | 0,93 | 1,54 | -0,61 | -0,43 | 0,03 | 1,10 | 0,03 |
| 6 | 1,56 | 1,76 | -0,20 | -0,49 | 0,08 | 1,27 | 0,05 |
| 7 | 3,61 | 1,98 | 1,62 | 1,48 | 0,02 | 3,46 | 0,01 |
| 8 | 4,87 | 2,19 | 2,67 | 1,36 | 1,73 | 3,55 | 0,36 |
| 9 | 0,73 | 2,40 | -1,66 | -0,94 | 0,53 | 1,46 | 0,72 |
| 10 | 1,56 | 2,60 | -1,04 | -1,63 | 0,35 | 0,97 | 0,23 |
| 11 | 3,31 | 2,79 | 0,51 | 0,54 | 0,00 | 3,33 | 0,00 |
| 12 | 5,24 | 2,98 | 2,26 | 2,71 | 0,20 | 5,69 | 0,04 |
| 13 | 1,38 | 3,17 | -1,79 | 2,04 | 14,66 | 5,21 | -2,78 |
| 14 | 1,90 | 3,35 | -1,45 | -0,85 | 0,36 | 2,51 | -0,32 |
| 15 | 2,44 | 3,53 | -1,10 | -2,85 | 3,09 | 0,68 | 0,72 |
(2.4.5)
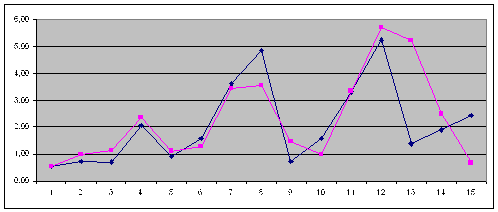
Рис. 2.4.10. Графік зміни коефіцієнта оборотністю постійних активів () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
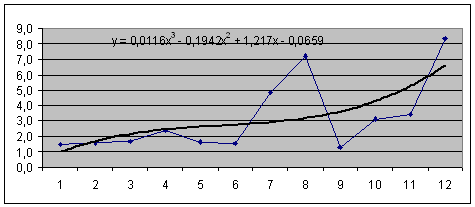
Рис. 2.4.11. Графік зміни коефіцієнта оборотністю запасів () та лінії тренда () з формулою.
Таблиця 2.4.6. Результат розрахунку числових значень коефіцієнта оборотності запасів.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 1,5 | 0,97 | 0,51 | 1,43 | 0,85 | 2,40 | 0,00 |
| 2 | 1,6 | 0,12 | 1,44 | 0,98 | 0,22 | 1,10 | 0,22 |
| 3 | 1,7 | 0,20 | 1,46 | 2,29 | 0,69 | 2,49 | 0,24 |
| 4 | 2,4 | 0,25 | 2,15 | 3,04 | 0,79 | 3,29 | 0,17 |
| 5 | 1,6 | 0,27 | 1,34 | 1,08 | 0,07 | 1,35 | 0,18 |
| 6 | 1,6 | 0,28 | 1,27 | 1,25 | 0,00 | 1,53 | 0,06 |
| 7 | 4,8 | 0,29 | 4,54 | 4,94 | 0,15 | 5,23 | 0,00 |
| 8 | 7,2 | 0,30 | 6,93 | 5,16 | 3,10 | 5,47 | 0,59 |
| 9 | 1,3 | 0,33 | 0,95 | 1,56 | 0,38 | 1,90 | 0,06 |
| 10 | 3,1 | 0,39 | 2,73 | 3,02 | 0,09 | 3,41 | 0,00 |
| 11 | 3,4 | 0,49 | 2,92 | 8,84 | 35,10 | 9,33 | 8,69 |
| 12 | 8,4 | 0,63 | 7,75 | 8,38 | 0,40 | 9,00 | 0,00 |
| 13 | 1,9 | 0,83 | 1,07 | 3,31 | 5,01 | 4,13 | -1,18 |
| 14 | 5,6 | 1,10 | 4,46 | 5,96 | 2,26 | 7,06 | -0,27 |
| 15 | 8,8 | 1,44 | 7,35 | 13,89 | 42,84 | 15,34 | -0,74 |
(2.4.6) 
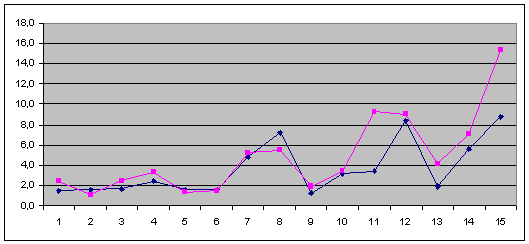Рис. 2.4.12. Графік зміни коефіцієнта оборотністю запасів () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()). 
Рис. 2.4.13. Графік зміни коефіцієнта ліквідності () та лінії тренда () з формулою.
Таблиця 2.4.7. Результат розрахунку числових значень коефіцієнта ліквідності.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 0,95 | 1,01 | -0,06 | -0,01 | 0,00 | 1,00 | 0,00 |
| 2 | 1,06 | 1,01 | 0,05 | 0,02 | 0,00 | 1,03 | 0,00 |
| 3 | 1,09 | 1,01 | 0,08 | -0,01 | 0,01 | 1,00 | 0,00 |
| 4 | 0,95 | 1,01 | -0,06 | 0,09 | 0,02 | 1,10 | 0,00 |
| 5 | 0,92 | 1,01 | -0,09 | 0,10 | 0,03 | 1,11 | 0,00 |
| 6 | 1,14 | 1,00 | 0,14 | -0,05 | 0,04 | 0,95 | 0,00 |
| 7 | 0,96 | 1,00 | -0,04 | -0,01 | 0,00 | 0,99 | 0,00 |
| 8 | 0,96 | 1,00 | -0,04 | -0,06 | 0,00 | 0,94 | 0,00 |
| 9 | 0,97 | 0,99 | -0,02 | 0,01 | 0,00 | 1,00 | 0,00 |
| 10 | 1,05 | 0,99 | 0,07 | 0,06 | 0,00 | 1,05 | 0,00 |
| 11 | 0,96 | 0,98 | -0,02 | -0,06 | 0,00 | 0,92 | 0,00 |
| 12 | 0,99 | 0,97 | 0,01 | -0,04 | 0,00 | 0,93 | 0,00 |
| 13 | 0,98 | 0,97 | 0,02 | 0,09 | 0,01 | 1,06 | -0,08 |
| 14 | 1,16 | 0,96 | 0,20 | -0,03 | 0,05 | 0,93 | 0,20 |
| 15 | 1,19 | 0,95 | 0,24 | -0,09 | 0,11 | 0,86 | 0,28 |
(2.4.7)
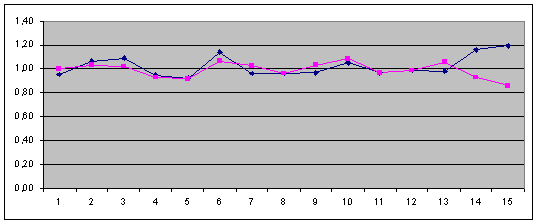
Рис. 2.4.14. Графік зміни коефіцієнта ліквідності () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
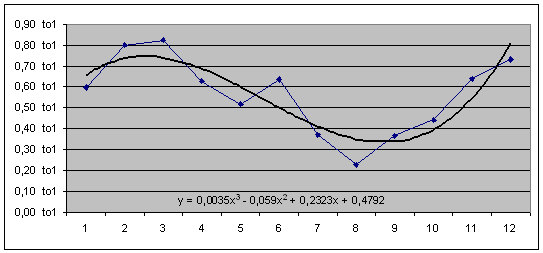
Рис. 2.4.15. Графік зміни коефіцієнта поточної ліквідності () та лінії тренда () з формулою.
Таблиця 2.4.8. Результат розрахунку числових значень коефіцієнта поточної ліквідності.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 0,60 | 0,66 | -0,06 | -0,01 | 0,00 | 0,65 | 0,00 |
| 2 | 0,80 | 0,74 | 0,06 | 0,01 | 0,00 | 0,74 | 0,00 |
| 3 | 0,83 | 0,74 | 0,09 | 0,02 | 0,00 | 0,76 | 0,01 |
| 4 | 0,63 | 0,69 | -0,06 | -0,05 | 0,00 | 0,64 | 0,00 |
| 5 | 0,52 | 0,60 | -0,09 | -0,01 | 0,01 | 0,59 | 0,01 |
| 6 | 0,64 | 0,51 | 0,13 | 0,07 | 0,00 | 0,57 | 0,01 |
| 7 | 0,37 | 0,41 | -0,04 | -0,01 | 0,00 | 0,41 | 0,00 |
| 8 | 0,23 | 0,35 | -0,13 | -0,11 | 0,00 | 0,24 | 0,00 |
| 9 | 0,37 | 0,34 | 0,02 | -0,04 | 0,00 | 0,31 | 0,01 |
| 10 | 0,44 | 0,40 | 0,04 | 0,11 | 0,00 | 0,51 | 0,01 |
| 11 | 0,64 | 0,55 | 0,08 | 0,08 | 0,00 | 0,63 | 0,00 |
| 12 | 0,73 | 0,82 | -0,09 | -0,10 | 0,00 | 0,72 | 0,00 |
| 13 | 0,69 | 1,22 | -0,53 | -0,17 | 0,13 | 1,05 | -0,51 |
| 14 | 0,97 | 1,77 | -0,80 | -0,03 | 0,60 | 1,75 | -0,79 |
| 15 | 0,98 | 2,50 | -1,52 | 0,16 | 2,83 | 2,66 | -1,72 |
(2.4.8)
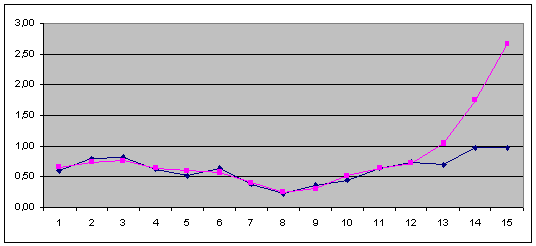
Рис. 2.4.16. Графік зміни коефіцієнта поточної ліквідності () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
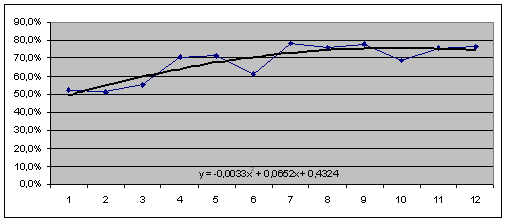
Рис. 2.4.17. Графік зміни коефіцієнта фінансового левериджу () та лінії тренда () з формулою.
Таблиця 2.4.9. Результат розрахунку числових значень коефіцієнта фінансового леверіджу.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 52,1% | 49,4% | 0,03 | 0,04 | 0,00 | 53,30% | 0,00 |
| 2 | 51,2% | 55,0% | -0,04 | -0,01 | 0,00 | 53,99% | 0,00 |
| 3 | 55,6% | 59,8% | -0,04 | -0,05 | 0,00 | 55,15% | 0,00 |
| 4 | 70,4% | 64,0% | 0,06 | 0,06 | 0,00 | 70,37% | 0,00 |
| 5 | 71,6% | 67,6% | 0,04 | 0,00 | 0,00 | 67,14% | 0,00 |
| 6 | 61,0% | 70,5% | -0,10 | -0,06 | 0,00 | 64,72% | 0,00 |
| 7 | 78,4% | 72,7% | 0,06 | 0,01 | 0,00 | 74,07% | 0,00 |
| 8 | 75,8% | 74,3% | 0,02 | 0,05 | 0,00 | 79,44% | 0,00 |
| 9 | 77,6% | 75,2% | 0,02 | -0,01 | 0,00 | 74,57% | 0,00 |
| 10 | 68,7% | 75,4% | -0,07 | -0,05 | 0,00 | 70,37% | 0,00 |
| 11 | 75,8% | 75,0% | 0,01 | -0,01 | 0,00 | 73,57% | 0,00 |
| 12 | 76,3% | 74,0% | 0,02 | 0,04 | 0,00 | 77,93% | 0,00 |
| 13 | 75,7% | 72,2% | 0,03 | 0,03 | 0,00 | 75,72% | 0,00 |
| 14 | 69,8% | 69,8% | 0,00 | -0,02 | 0,00 | 68,19% | 0,02 |
| 15 | 72,6% | 66,8% | 0,06 | -0,05 | 0,01 | 62,26% | 0,14 |
(2.4.9)
Рис. 2.4.18. Графік зміни коефіцієнта валового прибутку () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
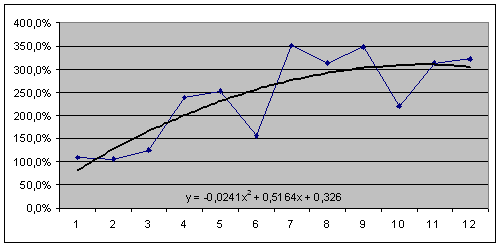
Рис. 2.4.19. Графік зміни коефіцієнта довгострокової заборгованості () та лінії тренда () з формулою.
Таблиця 2.4.10. Результат розрахунку числових значень коефіцієнта довгострокової заборгованості.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 108,6% | 81,8% | 0,27 | 0,02 | 0,06 | 83,68% | 0,06 |
| 2 | 104,8% | 126,2% | -0,21 | -0,01 | 0,04 | 125,50% | 0,04 |
| 3 | 125,0% | 165,8% | -0,41 | -0,09 | 0,10 | 156,57% | 0,08 |
| 4 | 238,3% | 200,6% | 0,38 | 0,30 | 0,01 | 230,11% | 0,00 |
| 5 | 252,7% | 230,6% | 0,22 | -0,05 | 0,07 | 225,95% | 0,03 |
| 6 | 156,2% | 255,7% | -0,99 | -0,37 | 0,39 | 218,71% | 0,25 |
| 7 | 351,0% | 276,0% | 0,75 | 0,16 | 0,34 | 292,40% | 0,10 |
| 8 | 313,7% | 291,5% | 0,22 | 0,58 | 0,12 | 349,06% | 0,04 |
| 9 | 347,4% | 302,2% | 0,45 | 0,05 | 0,16 | 307,30% | 0,05 |
| 10 | 219,8% | 308,0% | -0,88 | -0,63 | 0,06 | 244,57% | 0,03 |
| 11 | 313,4% | 309,0% | 0,04 | -0,43 | 0,22 | 266,51% | 0,07 |
| 12 | 322,1% | 305,2% | 0,17 | 0,47 | 0,09 | 352,68% | 0,03 |
| 13 | 311,5% | 296,6% | 0,15 | 0,94 | 0,62 | 390,56% | -0,25 |
| 14 | 231,1% | 283,2% | -0,52 | 0,36 | 0,78 | 319,50% | -0,38 |
| 15 | 265,6% | 265,0% | 0,01 | -0,67 | 0,46 | 197,99% | 0,25 |
(2.4.10)
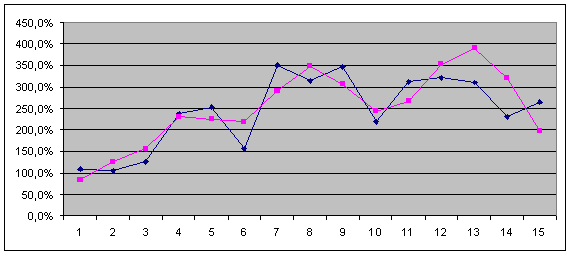
Рис. 2.4.20. Графік зміни коефіцієнта довгострокової заборгованості () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
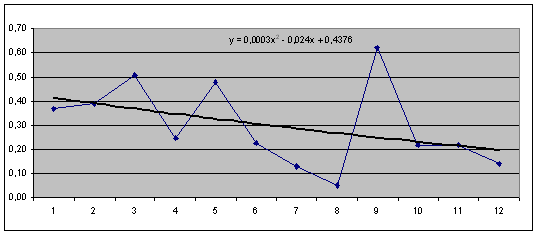
Рис. 2.4.21. Графік зміни коефіцієнта середнього періоду погашення дебіторської заборгованості () та лінії тренда () з формулою.
Таблиця 2.4.11. Результат розрахунку числових значень коефіцієнта середнього періоду погашення дебіторської заборгованості.
| X | K | Y | K-Y | y(x) | [(K-Y)-y(x)]^2 | Y+y(x) | (K-(Y+y(x))^2/K |
| 1 | 0,37 | 0,41 | -0,04 | -0,03 | 0,00 | 38,50% | 0,00 |
| 2 | 0,39 | 0,39 | 0,00 | 0,03 | 0,00 | 42,05% | 0,00 |
| 3 | 0,51 | 0,37 | 0,14 | -0,03 | 0,03 | 33,84% | 0,06 |
| 4 | 0,25 | 0,35 | -0,10 | -0,08 | 0,00 | 27,11% | 0,00 |
| 5 | 0,48 | 0,33 | 0,15 | 0,07 | 0,01 | 39,99% | 0,01 |
| 6 | 0,23 | 0,30 | -0,08 | 0,05 | 0,02 | 35,55% | 0,07 |
| 7 | 0,13 | 0,28 | -0,16 | -0,14 | 0,00 | 14,48% | 0,00 |
| 8 | 0,05 | 0,26 | -0,21 | -0,05 | 0,03 | 21,07% | 0,50 |
| 9 | 0,62 | 0,25 | 0,38 | 0,20 | 0,03 | 44,19% | 0,05 |
| 10 | 0,22 | 0,23 | -0,01 | 0,13 | 0,02 | 35,57% | 0,09 |
| 11 | 0,22 | 0,21 | 0,01 | -0,13 | 0,02 | 7,66% | 0,09 |
| 12 | 0,14 | 0,19 | -0,05 | -0,04 | 0,00 | 14,94% | 0,00 |
| 13 | 0,52 | 0,18 | 0,34 | 0,37 | 0,00 | 54,45% | -0,06 |
| 14 | 0,40 | 0,16 | 0,24 | 0,52 | 0,08 | 67,93% | -0,69 |
| 15 | 0,33 | 0,15 | 0,19 | 0,27 | 0,01 | 41,20% | -0,24 |
(2.4.11)
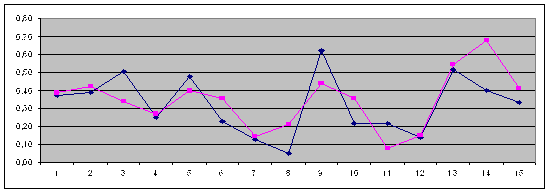
Рис. 2.4.22. Графік зміни коефіцієнта середнього періоду погашення дебіторської заборгованості () апроксимуючого графіка () та результатів перевірки якості прогнозування (після горизонтальної лінії ()).
Таблиця 2.4.12. Якість прогнозування фінансових коефіцієнтів
| Назва фінансового коефіцієнту | Якість прогнозування,% |
| коефіцієнт валового прибутку | 0,88672 |
| коефіцієнт прибутку до виплати відсотків і податків | 0,96132 |
| коефіцієнт аналізу операційних витрат | 0,99443 |
| коефіцієнт керуванням активами | 0,59102 |
| коефіцієнт оборотності постійних активів | 0,59051 |
| коефіцієнт оборотності запасів | 0,98711 |
| коефіцієнт ліквідності | 0,99999 |
| коефіцієнт поточної ліквідності | 0,99991 |
| коефіцієнт фінансового леверіджу | 0,99999 |
| коефіцієнт довгострокової заборгованості | 0,76730 |
| коефіцієнта середнього періоду погашення дебіторської заборгованості | 0,95165 |
Похожие работы
... ійного підвищення цін над зростанням її фізичного обсягу свідчить про підвищення попиту на неї); 2) відношення прибутку від реалізації продукції на зовнішньому ринку до обсягу її експорту (збільшення такого показника вказує на підвищення конкурентоспроможності продукції); 3) відношення обсягів реалізації експортної продукції до вартості матеріально-виробничих запасів (зменшення цього показника ...
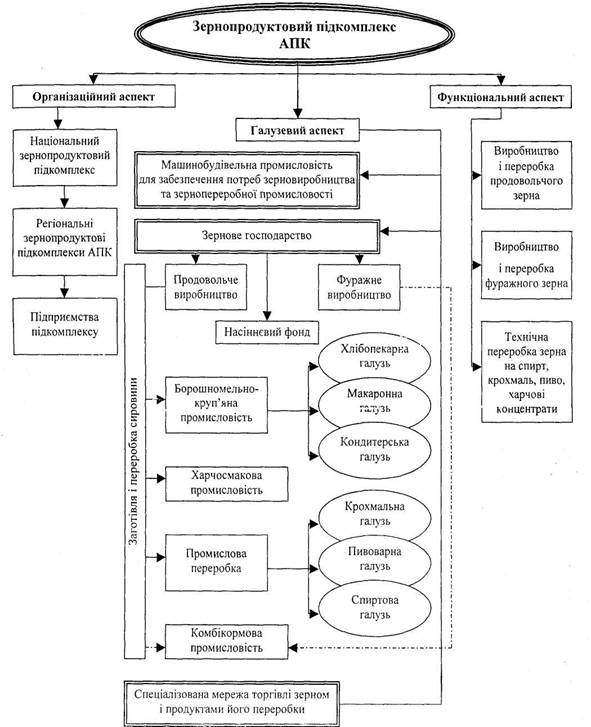
... яльність щодо зберігання зерна, міститься інформація про обсяги і рух зерна протягом місяця. Наступним заходом для створення організаційних умов конкурентоспроможного виробництва, формування рівноважного ринку зерна та налагодження діяльності зернопродуктового підкомплексу повинно відбутися врегулювання цін на зерно в післяжнивний період, що характеризується найбільшою диспропорційністю між міні ...
... підприємства - це покупка фірмою ТОВ «Граніт» у ВАТ “Запорізьке кар’єроуправління” в 2007 році гранітного кар'єру «Дніпропетровський-1» та початок ведення відбудовних робіт на його території. . Основне фінансування здійснюється за рахунок Статутного капіталу підприємства. Другорядним джерелом фінансування - є кредитування під заставу кар'єрної техніки. У перспективі, планується збувати продукц ...
... парка обладнання підприємства. Всі ці задачі розглядаються більш конкретно в наступному підрозділі роботи. 1.3 Проблеми законодавчого регулювання і стимулювання відновлення устаткування, як методу підвищення ефективності виробництва Науково-практичні завдання, що потребують рішення у процесі відновлення ОВФ в Україні, витікають з цілої низки взаємозалежних проблем, що виникають на усіх рівнях ...
0 комментариев