Статистика рынка товаров и услуг

1. Статистическая сводка. Группировка данных

Задание 1. Для целей анализа и сравнения применить характеристики центра группирования, к которым относятся средняя арифметическая, мода и медиана. Для характеристики степени отклонения распределения частот от симметричной формы рассчитать показатели эксцесса и ассиметрии. Проанализировать полученные значения показателей центра распределения и формы распределения. Сформулировать вывод.

Решение:

Величина равного интервала рассчитывается по формуле:

где k – число выделенных интервалов.

Определим длину интервала для денежных средств: d=(8854-1006)/5=1569.6(т.р.)

Мода – часто встречающаяся характеристика признака. Для дискретного вариационного ряда – наибольшая частота. Для интервального вариационного ряда мода рассчитывается по следующей формуле:

 - нижняя граница модального интервала

i– длина модального интервала

f_Mo – частота модального интервала

f_Mo+1 – частота интервала следующего за модальным

Модальный интервал – интервал с наибольшей частотой

х_Мо=1006; i_Mo =1962; f_Mo =16; f_Mo-1 =0; f_Mo+1 =6;

(т.р.)

Медиана – значение признака, делящее всю совокупность на две равные части. Интервальный вариационный ряд:

х_Ме – нижняя граница медианного интервала;

i – длина медианного интервала

 - накопленная частота интервала предшествующая медианному.

 - частота медианного интервала

Медианный интервал – первый интервал накопленная частота которого превышает половину от общей суммы частот.

х_Ме=1006; i_Mе =1962; f_Mе =16; f_Mе-1 =16, f=30.

Выявление общего характера распределения предполагает вычисление таких показателей распределение, как, асимметрия и эксцесс. Для симметричных распределений частоты двух вариант, равноотстоящих в обе стороны от центра распределения (вершины распределения), равны между собой. Для симметричных распределений совпадают между собой средняя, мода, медиана. Статистическим показателем, характеризующим асимметрию распределения, является относительный показатель асимметрии. Он рассчитывается по формуле:

=3556,6-2213,38=1343,22

 — среднее значение признака;

M_o – мода;

A_s- относительный показатель асимметрии.

Если A_s положителен, то распределение имеет правостороннюю асимметрию, и общая частота признаков справа от вершины больше общей частоты признака слева от вершины.

Соотношение моды, медианы и средней арифметической указывает на характер распределения и позволяет оценить его асимметрию. Так в симметричных распределениях все эти три характеристики равны между собой. Чем больше расхождение между модой и средней арифметической , тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней.

Эксцесс (Э) - показатель, характеризующий остроту вершины распределения. Если Э положительный, то распределение называется островершинным. Это означает, что частота появления наибольшего значения признака существенно больше частот появления всех других значений признака.

Если Э отрицателен, то это означает, что частота появления наибольшего значение признака в выбранной статистической совокупности не очень велика по сравнению с частотами появления всех других значений признаков.

Наиболее интересный случай, когда Э принимает нулевое значение. В этом случае говорят, что статистическая совокупность (признак) имеет нормальное распределение.

Задание 2. Для выявления зависимости между экономическими показателями деятельности предприятий провести аналитическую группировку показателей 30 предприятий. Группировку провести с равными интервалами, выделив четыре или пять групп. Рассчитать коэффициенты вариации по группировочному признаку на основании исходных данных и по аналитической группировке согласно своего варианта. Объяснить расхождения в значениях полученных коэффициентов.

Решение:

Распределим предприятия по группировочному признаку денежные средства.

Величина равного интервала рассчитывается по формуле:

где k – число выделенных интервалов.

Определим длину интервала для денежных средств, число групп зададим равное 4:

(т.р.)

Коэффициент вариации рассчитаем по формуле:

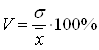
Для расчета средних величин используем формулы средней арифметической простой и взвешенной в зависимости от исходных данных.

Среднее квадратическое отклонение так же рассчитаем по формуле простой (при расчете по исходным данным) и взвешенной.

Рассчитаем коэффициенты для исходных данных и по аналитической таблице:

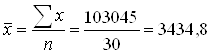
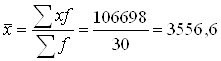
Среднее квадратическое отклонение:

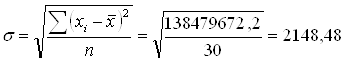
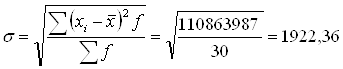
Рассчитаем коэффициент вариации:

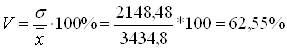
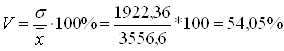
Вывод: в обоих расчетах коэффициент вариации значительно больше 33%. Следовательно, рассмотренная совокупность неоднородна и средняя для нее недостаточно типична.