Навигация
Статистическое изучение взаимосвязей
6. Статистическое изучение взаимосвязей
Задание 1. Для выявления зависимости между группировочным и результативным показателями рассчитайте линейный коэффициент корреляции по исходным данным своего варианта.
| № | Чистая прибыль отчетного периода, т.р. | Денежные средства, т.р. | № | Чистая прибыль отчетного периода, т.р. | Денежные средства, т.р. | № | Чистая прибыль отчетного периода, т.р. | Денежные средства, т.р. |
| 9 | 1523 | 1378 | 19 | 6154 | 6222 | 29 | 4589 | 1202 |
| 10 | 24971 | 1901 | 20 | 1170 | 8854 | 30 | 1579 | 7555 |
| 11 | 8124 | 6082 | 21 | 2189 | 1537 | 31 | 1570 | 4393 |
| 12 | 1478 | 1638 | 22 | 1776 | 3136 | 32 | 1321 | 4400 |
| 13 | 941 | 4999 | 23 | 1621 | 1006 | 33 | 1754 | 3650 |
| 14 | 18180 | 1576 | 24 | 9882 | 2232 | 34 | 3501 | 5718 |
| 15 | 3030 | 2387 | 25 | 1235 | 2810 | 35 | 2160 | 3417 |
| 16 | 13123 | 6031 | 26 | 8882 | 1277 | 36 | 2363 | 2942 |
| 17 | 2271 | 1299 | 27 | 4813 | 1085 | 37 | 1007 | 1972 |
| 18 | 2017 | 3757 | 28 | 1653 | 6701 | 38 | 1145 | 1888 |
| Итого | 136022 | 103045 | ||||||
Решение:
Предположим наличие линейной зависимости между рассматриваемыми признаками. Уравнение связи будет иметь следующий вид:
![]()

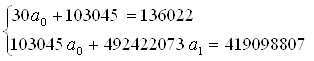
| Денежные средства, т.р., х | Чистая прибыль отчетного периода | x2 | xy | Yx | (x-xср)2 | (Y-Yср.)2 | (x-xср) * *(у-уср.) |
| 1378 | 1523 | 1898884,0 | 2098694,0 | 5248,7 | 4230563,4 | 9066522 | 6193262 |
| 1901 | 24971 | 3613801,0 | 47469871,0 | 5067,0 | 2352644,7 | 417668244 | -31346850 |
| 6082 | 8124 | 36990724,0 | 49410168,0 | 3614,3 | 7007491,4 | 12887621 | 9503152 |
| 1638 | 1478 | 2683044,0 | 2420964,0 | 5158,4 | 3228610,0 | 9339543 | 5491242 |
| 4999 | 941 | 24990001,0 | 4704059,0 | 3990,6 | 2446617,4 | 12910128 | -5620155 |
| 1576 | 18180 | 2483776,0 | 28651680,0 | 5179,9 | 3455261,4 | 186211497 | -25365516 |
| 2387 | 3030 | 5697769,0 | 7232610,0 | 4898,1 | 1097954,7 | 2262217 | 1576011 |
| 6031 | 13123 | 36372961,0 | 79144813,0 | 3632,0 | 6740081,4 | 73769776 | 22298302 |
| 1299 | 2271 | 1687401,0 | 2950029,0 | 5276,2 | 4561784,0 | 5121471 | 4833533 |
| 3757 | 2017 | 14115049,0 | 7577869,0 | 4422,1 | 103791,4 | 6335625 | -810915 |
| 6222 | 6154 | 38713284,0 | 38290188,0 | 3565,7 | 7768298,0 | 2624184 | 4515024 |
| 8854 | 1170 | 78393316,0 | 10359180,0 | 2651,2 | 29367367,4 | 11316945 | -18230438 |
| 1537 | 2189 | 2362369,0 | 3364493,0 | 5193,5 | 3601771,4 | 5499338 | 4450546 |
| 3136 | 1776 | 9834496,0 | 5569536,0 | 4637,9 | 89301,4 | 7606932 | 824202 |
| 1006 | 1621 | 1012036,0 | 1630726,0 | 5378,0 | 5899231,4 | 8485957 | 7075353 |
| 2232 | 9882 | 4981824,0 | 22056624,0 | 4952,0 | 1446808,0 | 28600391 | -6432672 |
| 2810 | 1235 | 7896100,0 | 3470350,0 | 4751,2 | 390416,7 | 10883841 | 2061367 |
| 1277 | 8882 | 1630729,0 | 11342314,0 | 5283,8 | 4656244,7 | 18904524 | -9382115 |
| 1085 | 4813 | 1177225,0 | 5222105,0 | 5350,5 | 5521716,7 | 77804 | -655447 |
| 6701 | 1653 | 44903401,0 | 11076753,0 | 3399,3 | 10667844,7 | 8300545 | -9410044 |
| 1202 | 4589 | 1444804,0 | 5515978,0 | 5309,9 | 4985544,7 | 3018 | -122657 |
| 7555 | 1579 | 57078025,0 | 11929345,0 | 3102,5 | 16975773,4 | 8732419 | -12175367 |
| 4393 | 1570 | 19298449,0 | 6897010,0 | 4201,2 | 918083,4 | 8785691 | -2840070 |
| 4400 | 1321 | 19360000,0 | 5812400,0 | 4198,7 | 931546,7 | 10323797 | -3101145 |
| 3650 | 1754 | 13322500,0 | 6402100,0 | 4459,3 | 46296,7 | 7728771 | -598178 |
| 5718 | 3501 | 32695524,0 | 20018718,0 | 3740,8 | 5212850,0 | 1067227 | -2358663 |
| 3417 | 2160 | 11675889,0 | 7380720,0 | 4540,3 | 318,0 | 5636193 | 42338 |
| 2942 | 2363 | 8655364,0 | 6951946,0 | 4705,3 | 242884,7 | 4713530 | 1069974 |
| 1972 | 1007 | 3888784,0 | 1985804,0 | 5042,3 | 2139881,4 | 12440199 | 5159511 |
| 1888 | 1145 | 3564544,0 | 2161760,0 | 5071,5 | 2392693,4 | 11485773 | 5242321 |
| 103045 | 136022 | 492422073 | 419098807 | 136022 | 138479672,2 | 908789722 | -48114093 |
n – число наблюдений; отсюда: а0= 5727,48; а1= -0,3474, т.к. ![]() <0 оценим связь как обратную.
<0 оценим связь как обратную.
Следовательно, уравнение корреляционной связи: yx=81,178х-37445,94
Рассчитаем линейный коэффициент корреляции по формуле:
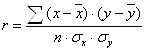
где ![]() - среднее квадратическое отклонение факторного и результативного признаков.
- среднее квадратическое отклонение факторного и результативного признаков.
![]()
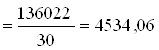
![]()
![]()

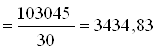
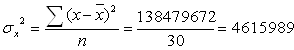
![]()
Таким образом, линейный коэффициент корреляции будет равен:
![]()
Вывод: Значение линейного коэффициента корреляции говорит о наличии слабой связи по шкале Чеддока и о том, что 13,6% изменений результата происходит под влиянием фактора.
Список литературы
1. Белявский И.К. и др. Статистика рынка товаров и услуг: Учебник. -М: Финансы и статистика, 1995.
2. Елисеева И.И, Юзбашев М.М. Общая теория статистики: Учебник. -М.: Финансы и статистика,1995.
3. Методические указания и решение типовых задач по статистике социально-экономической и отраслевой / Под ред. Т.Г. Храмцовой. - Новосибирск, 1990.
4. Ряузов Н.Н. Общая теория статистики: Учебник. -М.: Финансы и статистика, 1984.
5. Статистика: Учебно – методическое пособие/ Под ред. Т.Г. Храмцовой. - Новосибирск, 1999.
Похожие работы
... цен и ценообразования; изучение процессов товародвижения, товарооборота (продажи услуг), товарных запасов и товарооборачиваемости; оценка состояния и развития инфраструктуры рынка; выявление и анализ социально-экономических результатов и результативности функционирования рынка. 1.3. Система показателей статистики рынка В процессе реализации выдвинутых задач исследования рынка статистика ...
... импортных товаров с внутреннего рынка страны. Если говорить о положении на Воронежском потребительском рынке, то можно заметить, что за годы рыночных преобразований в торговле и бытовом обслуживании произошли некоторые перемены к лучшему. Потребительский рынок товаров и услуг стал более насыщенный, исчез дефицит на многие товары, ликвидированы очереди, наблюдается прирост торговой сети за счет ...
... подведомственной территории определяет особый интерес к нему со стороны органов местного самоуправления. На передний план выходят вопросы рационального управления развитием и состоянием рынка бытовых услуг на муниципальном уровне. Исследования, проведенные в работе, определили способы экономического регулирования рынка, которые целесообразно использовать на уровне муниципального управления. В ...
... исследуемых объектов, приводит к изменению установившихся причинно-следственных связей. Именно поэтому изучение структуры и структурных сдвигов занимает важное место в курсе теории статистики. В статистике под структурой понимают совокупность единиц, обладающих определенной устойчивостью внутригрупповых связей при сохранении основных признаков, характеризующих эту совокупность как целое. Основные ...

0 комментариев