Навигация
Решение СЛАУ методом Гаусса
4. Решение СЛАУ методом Гаусса
4.1 Теоретические сведения
Рассмотрим один из наиболее известных и широко применяемых прямых методов решения систем линейных уравнений. Обычно этот метод называют методом исключения или методом Гаусса.
Чтобы проиллюстрировать этот метод, рассмотрим сначала систему из трех уравнений с тремя неизвестными:
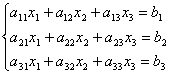 (4.1)
(4.1)
В такой системе по крайней мере один из коэффициентов ![]() ,
,![]() ,
,![]() должен быть отличен от нуля, иначе бы мы имели бы дело в этих трех уравнениях только с двумя неизвестными. Если
должен быть отличен от нуля, иначе бы мы имели бы дело в этих трех уравнениях только с двумя неизвестными. Если ![]() , то можно переставить уравнения так, чтобы коэффициент при
, то можно переставить уравнения так, чтобы коэффициент при ![]() в первом уравнении был отличен от нуля. Очевидно, что перестановка уравнений оставляет систему неизменной: ее решение остается прежним.
в первом уравнении был отличен от нуля. Очевидно, что перестановка уравнений оставляет систему неизменной: ее решение остается прежним.
Теперь введем множитель ![]() .
.
Умножим первое уравнение системы (4.1) на ![]() и вычтем его из второго уравнения системы. («Первое» и «второе» уравнения берем уже после перестановки, если она была необходима). Результат вычитания равен:
и вычтем его из второго уравнения системы. («Первое» и «второе» уравнения берем уже после перестановки, если она была необходима). Результат вычитания равен:
![]()
Так как
![]() ,
,
![]() фактически исключается из второго уравнения (именно для достижения такого результата и было выбрано значение
фактически исключается из второго уравнения (именно для достижения такого результата и было выбрано значение ![]() ).
).
Определим теперь новые коэффициенты
![]()
![]()
![]() .
.
Тогда второе уравнение системы приобретает вид
![]() (4.2)
(4.2)
Заменим второе из первоначальных уравнений уравнением (4.2) и введем множитель для третьего уравнения
![]() .
.
Умножим первое уравнение на этот множитель и вычтем его из третьего. Коэффициент при ![]() снова становится нулевым, и третье уравнение приобретает вид
снова становится нулевым, и третье уравнение приобретает вид
![]() (4.3)
(4.3)
где
![]()
![]()
![]() .
.
Если теперь в исходной системе уравнений (4.1) заменить третье уравнение на (4.3), то новая система выглядит так:
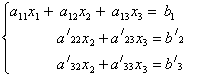 (4.4)
(4.4)
Эти новые уравнения полностью эквивалентны исходным уравнениям с тем преимуществом, что ![]() входит только в первое уравнение и не входит ни во второе, ни в третье. Таким образом, два последних уравнения представляют собой систему из двух уравнений с двумя неизвестными; если теперь найти решение этой системы, т.е. определить
входит только в первое уравнение и не входит ни во второе, ни в третье. Таким образом, два последних уравнения представляют собой систему из двух уравнений с двумя неизвестными; если теперь найти решение этой системы, т.е. определить ![]() и
и ![]() , то результат можно подставить в первое уравнение и найти
, то результат можно подставить в первое уравнение и найти ![]() . Иначе говоря, задача сведена к решению системы из двух уравнений с двумя неизвестными.
. Иначе говоря, задача сведена к решению системы из двух уравнений с двумя неизвестными.
Попытаемся теперь исключить ![]() из двух последних уравнений. Если
из двух последних уравнений. Если![]() , то снова мы переставим уравнения так, чтобы
, то снова мы переставим уравнения так, чтобы ![]() было отлично от нуля (если
было отлично от нуля (если ![]() и
и ![]() , то система вырождена и либо вовсе не имеет решения, либо имеет бесчисленное множество решений).
, то система вырождена и либо вовсе не имеет решения, либо имеет бесчисленное множество решений).
Введем новый множитель
![]() .
.
Умножим второе уравнение полученной системы (4.4) на ![]() и вычтем его из третьего. Результат вычитания равен
и вычтем его из третьего. Результат вычитания равен
![]()
В силу выбора![]()
![]() .
.
Полагая, что
![]()
окончательно получим
![]() (4.5)
(4.5)
Третье уравнение полученной системы (4.4) можно заменить уравнением (4.5), после чего система уравнений приобретает следующий вид:
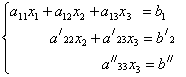 (4.6)
(4.6)
Такая система уравнений (4.6) иногда называется треугольной из-за своего внешнего вида.
Для решения необходимо определить ![]() из третьего уравнения системы (4.6), подставить этот результат во второе уравнение и определить
из третьего уравнения системы (4.6), подставить этот результат во второе уравнение и определить![]() . Полученные значения
. Полученные значения ![]() и
и![]() подставить в первое уравнение и определить
подставить в первое уравнение и определить![]() . Этот процесс, который обычно называется обратной подстановкой (обратный ход), определяется формулами:
. Этот процесс, который обычно называется обратной подстановкой (обратный ход), определяется формулами:
![]()
![]() (4.7)
(4.7)
![]() .
.
Необходимо отметить, если ![]() , то система уравнений вырождена.
, то система уравнений вырождена.
Теперь можно обобщить этот метод на случай системы из n – уравнений с n-неизвестными. Ниже записана система уравнений, приведенная к треугольному виду (4.8).
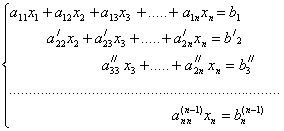 (4.8)
(4.8)
Формулы для вычисления неизвестных (обратный ход) будут иметь вид:
 (4.9)
(4.9)
4.2 Постановка задачи
Решение системы линейных алгебраических уравнений методом Гаусса.
4.3 Исходные данные
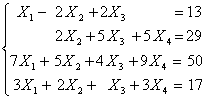
4.4 Блок-схема алгоритма
 | ||||||||
 | ||||||||
| ||||||||
Процедура для решения СЛАУ методом Гаусса
Похожие работы
... многих странах (в том числе развитых) применение компьютеров в управлении городскими территориями, ведении кадастра, анализе рыночных тенденций в рамках города весьма ограничено. В связи с этим выделим причины, по которым автоматизация решения типовых задач управления региональной недвижимостью Тульской области, как, впрочем, и других городов России, представляется весьма разумной: все материалы ...
... кадастра памятников России и привязки его к ГИС «Компас-2», я изучил возможности, функции ГИС «Компас-2», а также возможность использования его для создания различных видов природных кадастров. Компас-2 – это сетевая система для представления, моделирования и анализа географической информации Функциональные возможности системы КОМПАС 2: публикация географической информации (ГИ) в сетях ...
... информации. Набираемая информация отображается на дисплее, что позволяет контролировать ее правильность. Клавиатура и дисплей АИС должны быть независимыми от других навигационных устройств. Судовыми системами отображения АИС могут быть система отображения электронных карт (ECDIS, ECS, RCDS), РЛС, САРП или дисплей персонального компьютера. АИС и связанные с ней датчики информации питаются от ...
... де-факто, чему способствовала и их большая универсальность). Таким образом, именно Microsoft Excel был выбран мной для разработки средства автоматизации расчетов в лабораторной работе «Предварительные вычисления в триангуляции». Поэтому другие средства построения электронных таблиц здесь не рассматриваются, но зато уделяестся внимание некоторым специфичным средствам Excel. Возможности EXCEL ...
0 комментариев