Навигация
1. Общие сведения о волнах
1.1 Волновой процесс
Термины «волна», «волновой процесс», употребляемые в физике и технике, получили широкое распространение. Под распространением волны понимается постепенное вовлечение среды в некоторый физический процесс, приводящее к передаче энергии в пространстве.
Пусть в какой-то области пространства наблюдается физический процесс, который в точке ![]() можно охарактеризовать функцией
можно охарактеризовать функцией ![]() . В другой точке
. В другой точке ![]() измерения величины
измерения величины ![]() в это же время, быть может, покажут отсутствие процесса
в это же время, быть может, покажут отсутствие процесса![]() . Но через какое-то время он будет передан средой, и мы отметим, что
. Но через какое-то время он будет передан средой, и мы отметим, что ![]()
В простейшем случае будет обнаружено лишь запаздывание процесса во времени, т. е. ![]() , где
, где ![]() — время, требуемое для прохождения пути
— время, требуемое для прохождения пути ![]() со скоростью
со скоростью ![]() . Пусть в пространстве существует зависимость только от одной координаты
. Пусть в пространстве существует зависимость только от одной координаты ![]() . Характеризующая процесс функция
. Характеризующая процесс функция
![]() (1.1)
(1.1)
построена при ![]() и при
и при ![]() . Очевидно,
. Очевидно,![]()
![]() .
.
Говорят, что функция (1.1) описывает волну. Иногда волны этого рода называют «недеформируемыми»; имеется в виду, что временной закон во всех точках пространства — с точностью до сдвига ![]() — одинаков. Волна называется плоской и однородной. Дело в том, что, положив
— одинаков. Волна называется плоской и однородной. Дело в том, что, положив![]() , мы задаем плоскость, на которой мгновенное значение функции
, мы задаем плоскость, на которой мгновенное значение функции ![]() постоянно. Любую такую плоскость называют фронтом волны. В некоторый момент
постоянно. Любую такую плоскость называют фронтом волны. В некоторый момент ![]() фронт, для которого
фронт, для которого ![]() движется вдоль оси
движется вдоль оси ![]() со скоростью
со скоростью ![]() ,
,![]() . Плоскую однородную волну, распространяющуюся в противоположном направлении, следует описывать при помощи выражения (1.1) с изменением знака
. Плоскую однородную волну, распространяющуюся в противоположном направлении, следует описывать при помощи выражения (1.1) с изменением знака
![]() (1.1а)
(1.1а)
Обратимся к однородному волновому уравнению
![]() (1.2)
(1.2)
Если пользоваться декартовой системой координат ![]() и рассматривать только процессы, не зависящие от
и рассматривать только процессы, не зависящие от ![]() и
и ![]() , то волновое уравнение примет вид
, то волновое уравнение примет вид
![]() (1.3)
(1.3)
Путем непосредственной подстановки нетрудно убедиться, что функции, выражаемые формулами (1.1) и (1.1а), являются решениями одномерного волнового уравнения (1.3).
Общее решение уравнения (1.3) выражает формула
![]() (1.4)
(1.4)
где ![]() и
и ![]() — произвольные дважды дифференцируемые функции. Это наложение двух плоских однородных недеформируемых: волн, распространяющихся в противоположных направлениях.
— произвольные дважды дифференцируемые функции. Это наложение двух плоских однородных недеформируемых: волн, распространяющихся в противоположных направлениях.
1.2 Гармонические волны
Если в (1.1) взять такую функцию![]() , что
, что ![]() то в каждой точке пространства процесс будет иметь характер гармонических колебаний
то в каждой точке пространства процесс будет иметь характер гармонических колебаний
![]()
или
![]()
![]() (1.5)
(1.5)
Такого рода плоская однородная волна называется гармонической, а введенный параметр ![]() — волновым числом.
— волновым числом.
Как видно, полная фаза гармонических колебании в пространстве ![]() при заданном
при заданном ![]() убывает пропорционально
убывает пропорционально ![]() ; значения функции
; значения функции ![]() при этом периодически повторяются. Пространственный период называют длиной волны. Очевидно, для произвольного
при этом периодически повторяются. Пространственный период называют длиной волны. Очевидно, для произвольного ![]() должно быть
должно быть ![]()
![]() . Поэтому из (1.5) следует, что
. Поэтому из (1.5) следует, что ![]() , т. е.
, т. е.
![]() (1.6)
(1.6)
а также
![]() (1.7)
(1.7)
где ![]() —частота процесса.
—частота процесса.
Чтобы составить, более наглядное представление о гармонической волне, положим сначала ![]() и получим
и получим ![]() т.е. функцию, характеризующую распределение величины
т.е. функцию, характеризующую распределение величины ![]() вдоль оси
вдоль оси ![]() в начальный момент
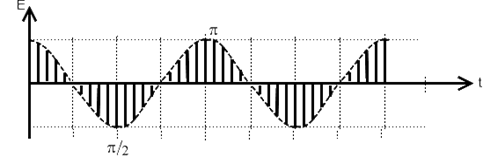
в начальный момент ![]() . Эта косинусоида (кривая на рис. 1.2а) представляет собой как бы «мгновенный снимок» процесса. Выберем следующий фиксированный момент
. Эта косинусоида (кривая на рис. 1.2а) представляет собой как бы «мгновенный снимок» процесса. Выберем следующий фиксированный момент ![]() и для него запишем
и для него запишем
![]()
где ![]() то есть не что иное, как расстояние, пройденное волной за истекшее время
то есть не что иное, как расстояние, пройденное волной за истекшее время ![]() . «Мгновенный снимок», соответствующий моменту
. «Мгновенный снимок», соответствующий моменту ![]() , дает, таким образом, косинусоиду, смещенную по оси
, дает, таким образом, косинусоиду, смещенную по оси ![]() на расстояние
на расстояние ![]() (кривая 2 на рис. 1.2а). Итак, распространение гармонической волны — это движение косинусоидального распределения и вдоль прямой с постоянной скоростью.
(кривая 2 на рис. 1.2а). Итак, распространение гармонической волны — это движение косинусоидального распределения и вдоль прямой с постоянной скоростью.
Плоская однородная гармоническая волна выражается одним из частных решений одномерного волнового уравнения (1.3). Метод комплексных амплитуд приводит (1.3) к виду
![]()
![]() (1.8)
(1.8)
Это не что иное, как одномерная форма уравнения Гельмгольца. Его общее решение можно выразить следующей суммой:
![]() (1.9)
(1.9)
(![]() и
и ![]() —комплексные константы:
—комплексные константы: ![]() и
и ![]() ).
).
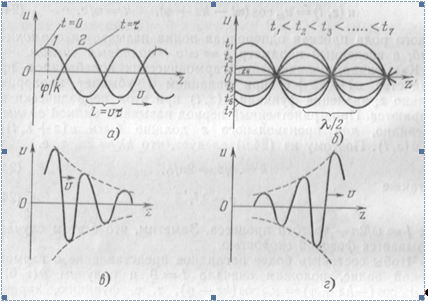
Рисунок 1.2
Умножая комплексную амплитуду ![]() на
на ![]() и отделяя вещественную часть, находим
и отделяя вещественную часть, находим
![]() (1.10)
(1.10)
Это наложение двух гармонических волн, распространяющихся в противоположных направлениях. Гармоническая волна, движущаяся вдоль оси ![]() , возникает как частное решение при
, возникает как частное решение при![]() .
.
В качестве другого частного решения рассмотрим наложение бегущих навстречу волн с одинаковыми амплитудами ![]() и начальными фазами
и начальными фазами ![]() . При этом из (1.10) получаем
. При этом из (1.10) получаем
![]() (1.11)
(1.11)
Такой процесс называется стоячей волной. Его отличительной особенностью является синфазность колебаний. Действительно, в каждой области постоянства знака множителя ![]() фаза зависит только от времени (это величина
фаза зависит только от времени (это величина ![]() или
или ![]() ). В зависимости от
). В зависимости от ![]() косинусоидального изменяется амплитуда гармонических колебаний
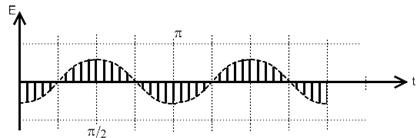
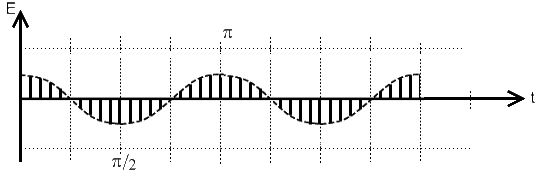
косинусоидального изменяется амплитуда гармонических колебаний ![]() . Ряд «мгновенных снимков» процесса для разных моментов времени дает картину, показанную на рис. 1.2б; косинусоидальное распределение и вдоль оси
. Ряд «мгновенных снимков» процесса для разных моментов времени дает картину, показанную на рис. 1.2б; косинусоидальное распределение и вдоль оси ![]() не движется (в отличие от бегущей волны), а испытывает «пульсации». При этом расстояния между соседними неподвижными нулями (узлами) равны
не движется (в отличие от бегущей волны), а испытывает «пульсации». При этом расстояния между соседними неподвижными нулями (узлами) равны ![]() ; таковы же и расстояния между соседними максимумами (пучностями).
; таковы же и расстояния между соседними максимумами (пучностями).
Похожие работы
... , то необходимость в дополнительной линии передачи вообще отпадает при передаче энергии на сотни километров, поскольку вся излучаемая энергия может быть перехвачена приемным устройством с апертурой приемлемых размеров. В диапазоне субмиллиметровых волн отношение допустимых размеров апертур к длине волны заметно уменьшается, тем не менее в ряде случаев подобные квазиоптические линии передачи могут ...
... в прямоугольном волноводе. КСВ равен отношению главных осей эллипса, величины которых соответствуют сумме и разности амплитуд падающей и отраженной волн. Таблица 1 Параметры измерительных линий Тип прибора Диапазон частот, ГГц Собственный КСВ Погрешность измерений КСВ, % (КСВ<2) Размеры сечения ВЧ-тракта, мм Р1-22 Р1-3 P1-7 Р1-20 Р1-13А 1-7,5 2,5-10,35 ...
... -зон 4 ГГц); - эквивалентная изотропно излучаемая мощность (ЭИИМ): дБВт; - полоса пропускания ствола: МГц ; - поляризация при передаче сигнала : круговая левая. Координаты земной станции спутниковой системы связи, расположенной в г. Киеве таковы: с.ш, в.д. 1.2.1. Определение угла места и азимута приёмной антенны земной станции Зная координаты ИСЗ, определим угол места и азимут А. При этом ...
... СОПРОВОЖДЕНИЕ (ферриты полностью размагничены). Отраженная от цели волна, вертикальной поляризации, проходя параболическое зеркало, падает на рефлектор, отражается с поворотом вектора поляризации на 90 град., и направляется на параболическое зеркало, отражается от него и фокусируется на облучателе, формируя на его выходах следующие ДН: - на выходе Σ (суммарного) канала -однолепестковая ДН ...
0 комментариев