Навигация
Метод измерения коэффициента отражения
3.3 Метод измерения коэффициента отражения
Задача измерения больших коэффициентов отражения актуальна при определении параметров короткозамкнутых нагрузок в волноводных трактах. Особенностью подобных измерений является большой динамический диапазон измеряемых величин, что затрудняет использование методов, связанных с применением измерительной линии ввиду сложности процедуры обеспечения квадратичности характеристики детектора в требуемом диапазоне. В настоящей работе теоретически и экспериментально обоснована методика измерения больших коэффициентов отражения на основе применения кольцевого резонатора бегущей волны.
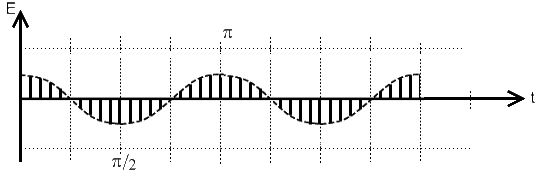
При широкодиапазонном возбуждении такого резонатора генератором качающейся частоты наблюдается чередование максимумов и минимумов амплитуды СВЧ-поля, как функция частоты возбуждения. Нетрудно показать, что соответствующие значения амплитуд определяются собственным затуханием линии α. Действительно, амплитуда в максимуме поля определяется, как результат интерференции волн, которые совершили целое число “оборотов” в кольцевой системе.
Е= ![]()
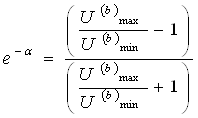
Так-как в максимуме поля j= 2kp. А в минимуме j= (2k+1)p/2, то
Емакс= Е0(1-e-α)-1
Емин= Е0(1+e-α)-
1
Если внести в кольцевую систему короткозамкнутую нагрузку, то её можно рассматривать, как отрезок короткозамкнутой линии, в которой установится режим стоячей волны в полном соответствии с рассмотренным во второй главе материалом. Тогда амплитуда поля в максимумах и минимумах аналогично рассмотренному выше для режима бегущих волн с учетом коэффициента отражения от обоих поверхностей представима в виде:
Емакс= Е0(1-Гe-α)-1,
Емин= Е0(1+Гe-α)-1.
Очевидно, что, исключив из уравнений параметры собственного затухания линии, можно определить модуль коэффициент отражения нагрузки Г.
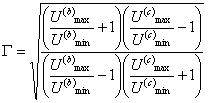
3.4 Реактивная нагрузка в линии
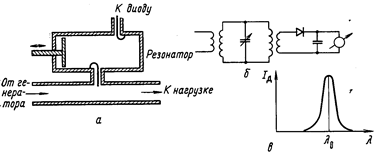
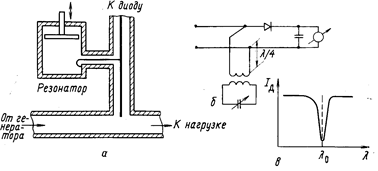
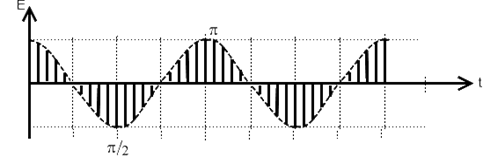
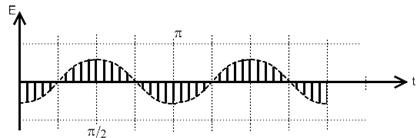
Известно, что внедрение диафрагмы в волновод эквивалентно включению в состав тракта реактивной нагрузки, характер которой определяется ориентацией диафрагмы относительно широкой стенки волновода. Данное обстоятельство позволяет судить о перспективности внедрения отражающей плоскости в кольцевой резонатор бегущей волны с целью его настройки – изменения. На рисунеке приведены осциллограммы частотной зависимости амплитуды поля при введении в зазор кольцевой системы диафрагмы ножевого типа.

Рисунок 3.5 Осциллограмма частотной зависимости амплитуды поля
Более высокие максимумы соответствуют режиму бегущей волны (а), низкие – дополнительные максимумы (б и в), возникающие при введении диафрагмы. Смещение начальных максимумов имеет место, однако составляет незначительную величину, в то время, как смещение побочных максимумов весьма значительно. На рисунке - б представлен случай введения диафрагмы параллельно широкой стенке, а на рисунке в – для случая введения диафрагмы параллельно узкой стенке. Очевидно, что в первом случае частота резонанса сдвигается в сторону низких частот, которые на осциллограмме слева, а во втором – в сторону высоких частот. При полном введении диафрагмы количество максимумов удваивается, и положения обоих добавочных максимумов совпадают. Таким образом, оказывается возможной настройка резонатора бегущей волны на любую частоту. Возможно также введение в волноводное кольцо диафрагмы, ножевая поверхность которой ориентирована перпендикулярно диагонали сечения волновода. В этом случае сопротивление носит чисто активный характер и влияет только на добротность резонатора.
Отмеченное свойство диафрагмы в кольцевой системе позволяет судить о возможности её применения не только для настройки резонатора, но и для целей согласования. Она может быть использована в качестве трансформатора сопротивления в волноводном тракте, в том числе – и в случае реактивной нагрузки для компенсации индуктивной либо емкостной составляющей. На представленных ниже зависимостях видно, что смещение начального максимума пренебрежимо мало и не превышает 5 МГц на основной частоте 7 ГГц.
3.5 Проверка аппаратной функции
При проведении измерений на установке данного типа появилась возможность определения зависимости и проверки аппаратной функции прибора измерения (Генератор качающейся частоты и индикатор КСВН и ослабления) в режиме бегущих волн. Аппаратная функция это закон по которому проходит измерение и изменение каких- либо параметров на конкретной установке, т. е. в нашем случае функция отклика системы на внешнее воздействие.
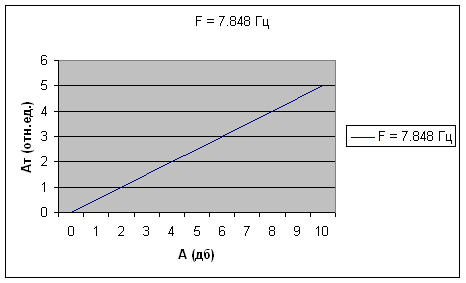
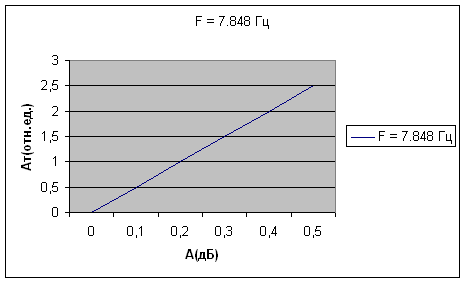
Для проведения эксперимента в нашу установку, в одно из плеч волноводноготракта был внедрен атенюатор поляризационного типа. Который осуществлял ослабление сигнала СВЧ . Измерения проводились на двух частотах: F1 = 8.355 Гц и F2 = 7.848 Гц. На установке регистрировались значения минимумов αmin(A) и максимумов αmax(A) при введении ослабления от 0 дБ до 10 дБ . Данные измерений приведены в таблице №1 и №2. Далее по этим измерениям были построены графики зависимости относительной величина Ат (отн.ед.) от ослабления аттенюатора A (дБ) в интервалах [0;1] и [0;10]. В ходе анализа графиков выяснилось, что с учетом погрешностей измерения и потерь, наблюдаемая нами зависимость практически линейна. Следовательно и линейна аппаратная функция установки .
A (дБ) – показания ослабления аттенюатора .
αmax(A) – положение максимума при заданной величине ослаблении.
αmin(A) – положение минимума при заданной величине ослаблении.
Ат (отн.ед.) – теоритическое значение величины ослабления.
Таблица данных №1.
F1 = 8.355 Гц
| A (дБ) | Ат (отн.ед.) | αmax(A) | αmin(A) |
| 0 | 0,489 | 5,10 | 1,225 |
| 1 | 1,052 | 2,50 | 1,210 |
| 2 | 1,479 | 1,90 | 1,195 |
| 3 | 1,876 | 1,60 | 1,175 |
| 4 | 2,057 | 1,50 | 1,160 |
| 5 | 2,645 | 1,32 | 1,145 |
| 6 | 3,206 | 1,22 | 1,125 |
| 7 | 3,358 | 1,19 | 1,110 |
| 8 | 3,637 | 1,17 | 1,110 |
| 9 | 3,709 | 1,15 | 1,095 |
| 10 | 4,016 | 1,13 | 1,090 |
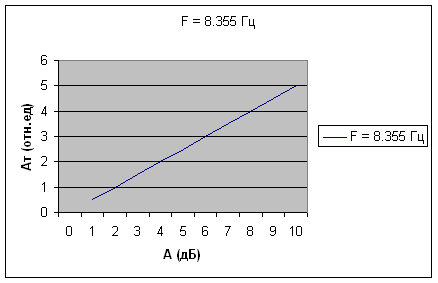 |
Таблица данных.
F2 = 7.848 Гц
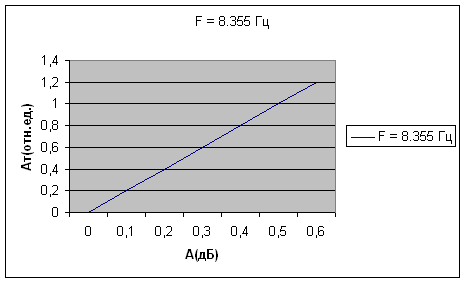
Таблица данных №2.
F1 = 7,848 Гц
| A (дБ) | Ат (отн.ед.) | αmax(A) | αmin(A) |
| 0 | 1,396 | 1,840 | 1,110 |
| 1 | 1,840 | 1,515 | 1,100 |
| 2 | 2,260 | 1,350 | 1,095 |
| 3 | 2,573 | 1,270 | 1,090 |
| 4 | 2,868 | 1,210 | 1,080 |
| 5 | 3,218 | 1,170 | 1,080 |
| 6 | 3,376 | 1,135 | 1,060 |
| 7 | 3,770 | 1,110 | 1,060 |
| 8 | 4,272 | 1,090 | 1,060 |
| 9 | 4,672 | 1,080 | 1,060 |
| 10 | 4,663 | 1,070 | 1,050 |
 |
Заключение
В работе экспериментально исследовалась частотная характеристика кольцевых (замкнутых) систем СВЧ - диапазона в режиме бегущих и стоячих волн. Показано, что в обоих случаях частотная зависимость является квазипериодической, причем, количество максимумов на ограниченном интервале для режима бегущих волн вдвое меньше, чем для режима стоячих волн. Экспериментально установлено, что добротность системы в режиме бегущих волн выше (примерно вдвое для рассматривавшейся системы), чем в режиме стоячих волн. На основании проделанных расчетов и экспериментальных исследований предложена методика (способ) определения больших коэффициентов отражения, что является актуальным для контроля качества короткозамыкателей СВЧ. Проведено практическое апробирование предложенной методики на образцах из различных материалов и получены частотные зависимости их коэффициента отражения в диапазоне от 6ГГц до 8,5 ГГц.
Исследовано влияние диафрагмирования волноводного кольца на характер частотной зависимости амплитуды волны в системе. Показано существенное влияние ориентация вводимой диафрагмы ножевого типа относительно широкой стенки волновода на положение максимумов амплитуды. Характер нагрузки при изменении положения диафрагмы изменяется от емкостного до индуктивного, а модуль сопротивления – от нуля до бесконечности, что позволяет производить перенастройку резонатора бегущей волны на любую частоту из рабочего диапазона, переходя от режима бегущих волн к режиму стоячих волн через режим смешанных волн. Проделанное экспериментальное исследование позволяет судить о перспективности использования режима бегущих волн в резонаторах СВЧ системах, по сравнению с традиционно применяющимися резонаторами, использующие стоячую волну.
Список использованных источников
1. Гуреев А.В.// Радиотехника и электроника (Москва).- 1994 -39 №6.- С.929-936
2. Ковалёв С. В., Нестеров С. М., Скородумов И. А. // Радиотехника и электроника (Москва)- 1993.- 38 №12.- С. 2138- 2140
3. Кирочкин Ю. А., Степанов К.Н. // Журнал экспериментальной и технической физики- 1993.- 104, №6.- С. 3955-3970.
4. Кубышкин Е. И. // Изв. РАН. Мех. тверд. тела.- 1992, №6.- С.- 42- 47.
5. Семин И. А. // Радиотехника и электроника.- 1993.- 38, №3.- С. 436- 439.
6. Свешников А. Г., Боголюбов А. Н., Минаев Д. В., Сычкова А. В. // Радиотехника и электроника – 1993.- 38 №5.- С. 804- 810
7. Кириленко А. А., Сенкевич С. Л., Тысик Б. Г.// Радиотехника и электроника (Москва).- 1990.- 35, №4.- С. 687- 694.
8. Козлова А. Н., Эткин В. С. // Журнал “Успехи физических наук”
9. Под редакцией Валитова Р. А. и Макаренко Б. И.// Измерения на миллиметровых и субмиллиметровых волнах (Москва).- 1984.-с. 91- 98.
10. Каценеленбаум Б. З. // Нерегулярные волноводы с медленно меняющимися параметрами.- М.: Изд- во АН СССР, 1961.- с.196.
11. Ваганов Р. Б., Матвеев Р. Ф., Мериакри В. В. // Многоволновые волноводы со случайными нерегулярностями.- М.: Сов.радио, 1972.- с.232.
12. Под редакцией Гроднева В.А. .. Многоволноводные круглые волноводы.- М.: Связь, 1972.- с. 198.
13. Валитова Р. А. // Методы и техника. М.: Радио и техника, 1984.- с.296
14. Вамберский М. В., Казанцев В. И., Шелухин С. А. // Передающие устройства СВЧ.- Москва «высшая школа»,1984.- с.57-74
15. Под ред. Мириманова // Миллиметровые и субмиллиметровые волны. Изд- во иностранной литературы.
16. Куликов Мю Н., Стальмахов В. С. // К расчету электронно- волнового усилителя типа М с тонким лучом. Радиотехника и электроника, 1964, т. 11, №2.-с. 252.
17. Лошаков Л. Н. // К теории электронного прибора СВЧ с взаимодействием в поперечном направлении. Радиотехника и электроника, 1960, т.5, №9.-с.1448.
18. Лошаков Л. Н. // О применении леммы Лоренца для приближенного расчета постоянных распространения в электронном приборе типа лампы с поперечным взаимодействием. Радиотехника и электроника, 1961, т.6, №12.-с.2012.
19. Лопухин В. М. // Возбуждение э\м колебаний и волн электронными потоками. Гостехиздат, 1953.
20. Под ред. Федотова // Электронные СВЧ приборы со скрещенными полями. Изд- во ин. лит., 1961.
Приложение
Таблица.1 Исследование параметров волны в линии при введении нагрузки параллельно узкой стенке
| № | L (мм) | f | f | Амплитуда волны | |
| f (db) | f | ||||
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 7,175 | 7,175 | 0 | 0 |
| 2 | 0,4 | 7,178 | 7,178 | 0 | 0 |
| 3 | 0,8 | 7,184 | 7,176 | -0,5 | -7,5 |
| 4 | 1,1 | 7,194 | 7,173 | -4,5 | -9 |
| 5 | 1,2 | 7,204 | 7,175 | -7 | -8 |
| 6 | 1,6 | 7,218 | 7,177 | -5 | -5 |
| 7 | 2 | 7,224 | 7,178 | -4 | -4,5 |
| 8 | 2,4 | 7,227 | 7,178 | -3 | -4 |
| 9 | 2,8 | 7,229 | 7,177 | -3 | -4,2 |
| 10 | 3 | 7,232 | 7,178 | -3,2 | -5 |
Таблица 2 Исследование параметров волны в линии при введении нагрузки параллельно узкой стенке
| № | L (мм) | f | f | Амплитуда волны | |
| f | f | ||||
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 7,690 | 7,690 | 0 | -9,8 |
| 2 | 0,4 | 7,692 | 7,688 | -0,2 | -9 |
| 3 | 0,8 | 7,697 | 7,682 | -1,6 | -7,8 |
| 4 | 1,1 | 7,710 | 7,683 | -8 | -8,2 |
| 5 | 1,2 | 7,715 | 7,685 | -7,9 | -8,1 |
| 6 | 1,6 | 7,730 | 7,685 | -7,8 | -8 |
| 7 | 2 | 7,739 | 7,686 | -8 | -7 |
| 8 | 2,4 | 7,774 | 7,688 | -7,4 | -5,6 |
| 9 | 2,8 | 7,745 | 7,692 | -6 | -5,6 |
| 10 | 3 | 7,745 | 7,693 | -5,5 | -5,7 |
Таблица 3 Исследование параметров волны в линии при введении нагрузки параллельно узкой стенке
| № | L (мм) | f | f | Амплитуда волны | |
| f | f | ||||
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 8,225 | 8,225 | 0 | 0 |
| 2 | 0,4 | 8,226 | 8,228 | 0 | 0 |
| 3 | 0,8 | 8,232 | 8,225 | -1 | -9,8 |
| 4 | 1,1 | 8,246 | 8,223 | -6,8 | -10 |
| 5 | 1,2 | 8,250 | 8,225 | -8 | -11 |
| 6 | 1,6 | 8,273 | 8,226 | -10,2 | -11,3 |
| 7 | 2 | 8,287 | 8,227 | -10 | -10 |
| 8 | 2,4 | 8,287 | 8,228 | -9 | -9,8 |
| 9 | 2,8 | 8,288 | 8,229 | -8 | -8,8 |
Таблица 4 Исследование параметров волны в линии при введении нагрузки параллельно широкой стенке
| № | L (мм) | f | f | Амплитуда волны | |
| f | f | ||||
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 8,228 | 8,228 | 0 | 0 |
| 2 | 0,3 | 8,220 | 8,220 | -3 | -3 |
| 3 | 0,6 | 8,201 | 8,222 | -5,2 | -8,8 |
| 4 | 0,9 | 8,194 | 8,224 | -5,1 | -10 |
| 5 | 1,2 | 8,182 | 8,230 | -5,4 | -11,8 |
| 6 | 1,5 | 8,179 | 8,234 | -4,8 | -8 |
Таблица .5 Исследование параметров волны в линии при введении нагрузки параллельно широкой стенке
| № | L (мм) | f | f | Амплитуда волны | |
| f | f | ||||
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 7,691 | 7,691 | 0 | 0 |
| 2 | 0,3 | 7,684 | 7,684 | -2,2 | -2,2 |
| 3 | 0,6 | 7,674 | 7,687 | -9 | -7,6 |
| 4 | 0,9 | 7,663 | 7,687 | -10,3 | -8,9 |
| 5 | 1,2 | 7,652 | 7,692 | -9,5 | -9,5 |
| 6 | 1,5 | 7,646 | 7,694 | -9 | -9 |
Таблица 6 Исследование параметров волны в линии при введении нагрузки параллельно широкой стенке
| № | L (мм) | f | f | Амплитуда волны | |
| f | f | ||||
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 7,188 | 7,188 | 0 | 0 |
| 2 | 0,3 | 7,179 | 7,188 | -7 | -4 |
| 3 | 0,6 | 7,172 | 7,188 | -9 | -7,3 |
| 4 | 0,9 | 7,156 | 7,188 | -9,2 | -8 |
| 5 | 1,2 | 7,145 | 7,188 | -9,2 | -9,2 |
| 6 | 1,5 | 7,138 | 7,190 | -8,2 | -8,2 |
Похожие работы
... , то необходимость в дополнительной линии передачи вообще отпадает при передаче энергии на сотни километров, поскольку вся излучаемая энергия может быть перехвачена приемным устройством с апертурой приемлемых размеров. В диапазоне субмиллиметровых волн отношение допустимых размеров апертур к длине волны заметно уменьшается, тем не менее в ряде случаев подобные квазиоптические линии передачи могут ...
... в прямоугольном волноводе. КСВ равен отношению главных осей эллипса, величины которых соответствуют сумме и разности амплитуд падающей и отраженной волн. Таблица 1 Параметры измерительных линий Тип прибора Диапазон частот, ГГц Собственный КСВ Погрешность измерений КСВ, % (КСВ<2) Размеры сечения ВЧ-тракта, мм Р1-22 Р1-3 P1-7 Р1-20 Р1-13А 1-7,5 2,5-10,35 ...
... -зон 4 ГГц); - эквивалентная изотропно излучаемая мощность (ЭИИМ): дБВт; - полоса пропускания ствола: МГц ; - поляризация при передаче сигнала : круговая левая. Координаты земной станции спутниковой системы связи, расположенной в г. Киеве таковы: с.ш, в.д. 1.2.1. Определение угла места и азимута приёмной антенны земной станции Зная координаты ИСЗ, определим угол места и азимут А. При этом ...
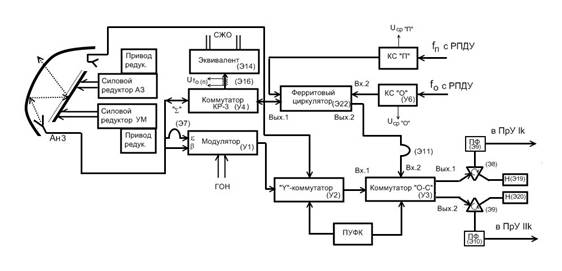
... СОПРОВОЖДЕНИЕ (ферриты полностью размагничены). Отраженная от цели волна, вертикальной поляризации, проходя параболическое зеркало, падает на рефлектор, отражается с поворотом вектора поляризации на 90 град., и направляется на параболическое зеркало, отражается от него и фокусируется на облучателе, формируя на его выходах следующие ДН: - на выходе Σ (суммарного) канала -однолепестковая ДН ...
0 комментариев