Навигация
Минимизация функции многих переменных. Приближённые численные методы. Метод Монте-Карло
Минимизация функции многих переменных. Приближённые численные методы. Метод Монте-Карло
1. Минимизация функции многих переменных. Аналитические методы.
Теорема Вейерштрасса: пусть ![]() - множество функций непрерывных на замкнутом ограниченном множестве
- множество функций непрерывных на замкнутом ограниченном множестве ![]() . Если
. Если ![]() , тогда
, тогда ![]() достигает своих наибольшего и наименьшего значений.
достигает своих наибольшего и наименьшего значений.
Определение: точки максимума и минимума называются точками экстремума функции. Теорема Ферма: (необходимое условие существования экстремума). Пусть функция ![]() - определена в окрестности точки
- определена в окрестности точки ![]() . Если
. Если ![]() - является точкой экстремума функции
- является точкой экстремума функции ![]() , и в этой точке существуют частные производные, тогда
, и в этой точке существуют частные производные, тогда
![]() (1)
(1)
Обобщение: если ![]() - точка экстремума, то в этой точке либо выполняется формула (1), либо производная не определена. Определение: точки, в которых выполняется условие (1), называются точками экстремума функции
- точка экстремума, то в этой точке либо выполняется формула (1), либо производная не определена. Определение: точки, в которых выполняется условие (1), называются точками экстремума функции ![]() . Сейчас изложим достаточные условия существования экстремумов функции многих переменных. Для этого вспомним некоторые сведения из теории квадратичных форм.
. Сейчас изложим достаточные условия существования экстремумов функции многих переменных. Для этого вспомним некоторые сведения из теории квадратичных форм.
Определение: квадратичная форма
![]() (2)
(2)
![]() (3)
(3)
называется положительно (отрицательно) определённой, если ![]() (соответственно
(соответственно ![]() ) для любого
) для любого ![]() , при условии
, при условии ![]() , и обращается в ноль, только при
, и обращается в ноль, только при ![]() .
.
Пример:
1) ![]() - положительно-определённая форма.
- положительно-определённая форма.
2) ![]() - не является положительно-определённой, хотя
- не является положительно-определённой, хотя ![]() , т.к.
, т.к. ![]() .
.
3) ![]() - отрицательно-определённая форма.
- отрицательно-определённая форма.
Определение: квадратичную форму, которая принимает как положительные, так и отрицательные значения называют неопределённой формой.
Пример:
4)![]() - неопределённая квадратичная форма.
- неопределённая квадратичная форма.
Теперь, мы уже можем сформулировать достаточные условия существования экстремумов для функции многих переменных.
Теорема: пусть ![]()
![]() , и пусть
, и пусть ![]() является критической точкой функции
является критической точкой функции ![]() . Если квадратичная форма
. Если квадратичная форма
![]() (4)
(4)
(т.е. второй дифференциал функции ![]() в точке
в точке ![]() ) является положительно-определённой (отрицательно-определённой) квадратичной формой, то точка
) является положительно-определённой (отрицательно-определённой) квадратичной формой, то точка ![]() - является точкой минимума (соответственно максимума). Если же квадратичная форма (4) является неопределённой, то в точке
- является точкой минимума (соответственно максимума). Если же квадратичная форма (4) является неопределённой, то в точке ![]() - экстремума нет.
- экстремума нет.
На вопрос: когда квадратичная форма является положительно (или отрицательно) определённой, отвечает критерий Сильвестра:
Для того, чтобы квадратичные формы (2),(3) были положительно-определёнными, необходимо и достаточно, чтобы
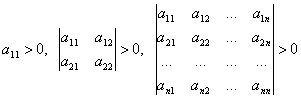 (5)
(5)
Для того, чтобы квадратичная форма (2), (3) была отрицательно-определённой, необходимо и достаточно, чтобы
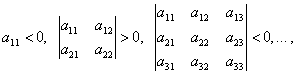 (6)
(6)
 (7)
(7)
Как видим, для нахождения точек экстремума нам нужно решать систему, в общем, нелинейных уравнений (1), а для выяснения характера точки экстремума нужно на основе критерия Сильвестра проверять условия (5), (6) и (7) для дифференциальной квадратичной формы (4) в точке экстремума. Проиллюстрируем этот метод на примере 5: Функция двух переменных:
![]() (8)
(8)
Решение: найдём критические точки:
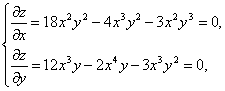 (9)
(9)
откуда получаем критические точки: А(0;0); В(3;2). Исследуем эти точки. Для этого нам нужно выяснить, в каждой из этих точек, к какому виду принадлежит квадратичная форма:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
В точке A(0;0) имеем:
![]() ,
,
так что ![]() , и условия критерия
, и условия критерия
Сильвестра не дают ответа на вопрос о наличии экстремума в этой точке.
Для решения этого вопроса надо привлечь старшие производные и формы более высокого порядка, для которых соответствующей общей теории пока нет, поэтому нужно обращаться к численным исследованиям.
В точке B(3;2) имеем:
![]() ,
,
получаем матрицу квадратичной формы:
![]() .
.
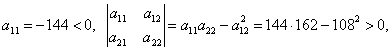
т.е. по критерию Сильвестра B(3;2) является точкой максимума: ![]()
Похожие работы
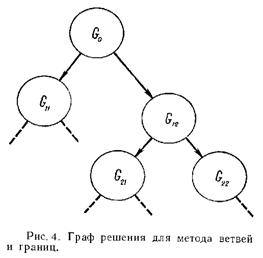
... (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи. 4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы 4.1 Формализация вычислительного процесса и рабочей нагрузки Узел вычислительной системы представляется в виде совокупности оборудования и ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
0 комментариев