Граничные условия

1.2 Граничные условия

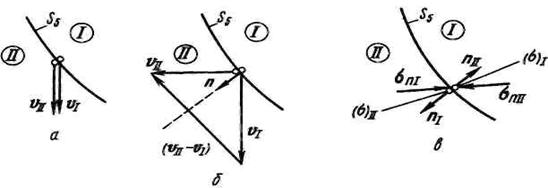
Рассмотрим граничные условия на границе раздела сред при распространении упругой волны. Они заключаются в непрерывности компонент вектора смещения и непрерывности нормального  и касательных ,  компонент тензора напряжений при переходе через границу раздела сред.

В изотропной среде компоненты тензора напряжений  связаны с компонентами тензора деформаций  при помощи закона Гука (1.6), а компоненты тензора деформаций  связаны с компонентами вектора смещений  с помощью формулы (1.3). Рассмотрим цилиндрическую границу в цилиндрической системе координат. Если систему прямоугольных координат  выбрать таким образом, что ось z является осью цилиндра, то компоненты тензора напряжений выразятся через компоненты вектора смещения по формулам:

, (1.10)

где - нормальная компонента тензора напряжений,  - касательные компоненты,  и  - упругие константы Ламе.

2. РАССЕЯНИЕ ПЛОСКОЙ ПРОДОЛЬНОЙ УПРУГОЙ ВОЛНЫ ОДНОРОДНЫМ ИЗОТРОПНЫМ ЦИЛИНДРИЧЕСКИМ СЛОЕМ

2.1 Постановка задачи

Рассмотрим бесконечный изотропный полый круговой цилиндр с внешним радиусом  и внутренним - , модули упругости и плотность материала которого  . Цилиндрическая система координат  выбрана таким образом, что координатная ось z является осью вращения цилиндра. Будем считать, что окружающее и находящееся в полости упругие среды являются изотропными и однородными, имеющими плотности  и модули упругости ,  соответственно.

Пусть из полупространства  на упругий цилиндрический слой параллельно оси Ох в плоскости Оxy падает плоская упругая монохроматическая волна:

Определим отраженную от слоя и прошедшую через слой волны, а также найдем поле смещений внутри упругого слоя.

Фронт падающей волны перпендикулярен образующим цилиндра и поэтому задача является плоской, то есть смещения не зависят от координаты z.

Учтем, что в формуле , представляющей собой общее выражение для смещения, потенциал  в силу выбранной системы координат мы выбрали так, чтобы единственной отличной от нуля была компонента . Поэтому в силу линейности задачи мы можем рассматривать отдельно падение продольной волны , сдвиговой волны , где .

Мы осстановимся на рассмотрении рассеяния плоской продольной волны, представленной вектором падения: .

2.2 Рассеяние продольной волны

Пусть из внешнего пространства на упругий цилиндр перпендикулярно падает плоская упругая продольная волна, потенциал смещений которой равен:

,

где - волновой вектор,  - радиус-вектор,  - круговая частота. В дальнейшем временную зависимость  для простоты формул опускаем. В цилиндрической системе координат падающая волна может быть представлена в виде:

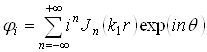, (2.1)

где - волновое число равное модулю вектора , , - цилиндрическая функция Бесселя порядка n.

Определим отраженную от цилиндра и возбужденную в полости волны, а также найдем потенциалы смещений внутри слоя.

Вектор смещения в однородных изотропных средах также будет иметь всего две отличные от нуля компоненты:

 

Отраженная, возбужденная упругие волны, а также волны внутри однородного слоя являются решениями уравнений Гельмгольца. Причем их потенциалы также удовлетворяют уравнениям Гельмгольца и не зависят от координаты z. Следует иметь в виду, что вектор-функция  будет иметь лишь одну отличную от нуля компоненту , то есть .

Отраженная волна должна удовлетворять условиям излучения на бесконечности:

, (2.2)

а прошедшая волна – условию ограниченности. Поэтому потенциалы смещений этих волн будем искать в виде:

- для отраженной волны:

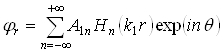, (2.3)

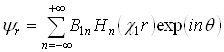
- для возбужденной волны:

, (2.4)

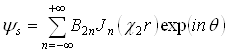
- для волны внутри слоя:

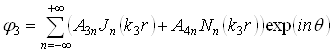 (2.5)

где , , 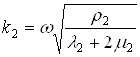, , 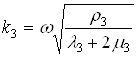, 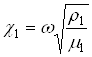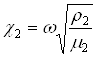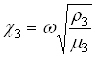- волновые числа.

Заметим, что представления (2.3) - (2.5) можно получить, применив метод разделения переменных к уравнениям Гельмгольца для потенциалов в цилиндрической системе координат от двух переменных. Мы получим функции вида:

.

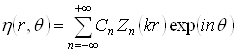Для того, чтобы потенциал отраженной волны удовлетворял условию излучения на бесконечности, необходимо в качестве цилиндрической функции Бесселя  выбрать цилиндрическую функцию Ханкеля первого рода , в этом случае потенциалу соответствует расходящейся волне с учетом того, что временной множитель выбран в виде . Для того, чтобы потенциал прошедшей волны удовлетворял условию ограниченности, необходимо в качестве цилиндрической функции Бесселя  выбрать цилиндрическую функцию Бесселя первого рода .  - цилиндрическая функция Неймана.

Коэффициенты подлежат определению из граничных условий, которые заключаются в непрерывности смещений и напряжений на обеих поверхностях упругого слоя. Имеем:

при : , , , ;

при : , , , ; (2.6)

где - компоненты вектора смещения частиц,  - компоненты тензора напряжений в средах  (j=1) ,  (j=2),  (j=3) соответственно.

Компоненты вектора смещения  связаны с потенциалами смещений следующим образом:

 (2.7)

Подставим (2.7) в (1.10), получим:

С учетом того, что дифференцирование по  - это умножение на , перепишем наши формулы:

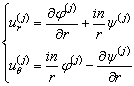 и

Подставим полученные выражения в граничные условия (2.6). В результате получим систему линейных алгебраических уравнений для коэффициентов :

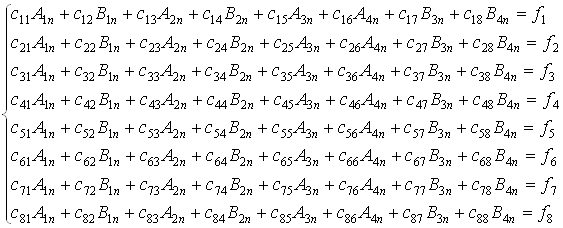
Разрешая для каждого n полученную систему одним из численных методов и подставляя полученные коэффициенты в потенциалы, найдем волновое поле, в том числе и в бесконечности.

Проведя вычисления для достаточно большого числа n, получаем возможность анализировать волновые поля вне и внутри оболочки по разложениям (2.2), (2.4), (2.5). В частности можно оценить поведение рассеянного поля в дальней зоне. Пользуясь асимптотическим представлением функций Ханкеля при больших значениях аргумента, для потенциала рассеянной продольной волны при  получим:

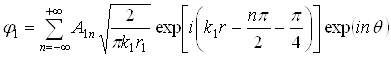
или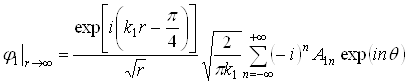

Опуская первый множитель, характеризующий распространение ненаправленной цилиндрической волны, и учитывая, что амплитуда падающей волны – единичная, получим выражение для нормированной амплитуды рассеянной волны:

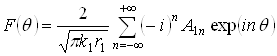 (2.8)

Это выражение определяет диаграмму направленности рассеянного поля по амплитуде.