Навигация
Формування ізоквант виробничої функції
1.3 Формування ізоквант виробничої функції
Розглянемо приклад, коли підприємство використовує два змінних ресурси — працю (L) і капітал (К). Виробнича функція з двома факторами виробництва (працею і капіталом) записується такою формулою:
Q=f(L,K)(1.5)
Для прикладу наведемо в табл. 1.1 різні обсяги випуску за різних комбінацій двох змінних ресурсів.
Таблиця 1.1 Обсяги випуску при використанні двох змінних ресурсів
| Затрати капіталу | Затрати праці | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 10 | 30 | 45 | 55 | 60 |
| 2 | 30 | 50 | 65 | 75 | 80 |
| 3 | 45 | 65 | 80 | 90 | 95 |
| 4 | 55 | 75 | 90 | 100 | 105 |
| 5 | 60 | 80 | 95 | 105 | 110 |
Цифра 10 першого стовпчика означає, що при застосуванні однієї одиниці капіталу та однієї одиниці праці максимальний (технологічно-ефективний) обсяг випуску дорівнюватиме 10 одиницям, а, наприклад, при застосуванні трьох одиниць праці і п'яти одиниць капіталу, максимальний обсяг випуску становитиме 95 одиниць і т. ін.
Рухаючись зліва направо по рядку, можна спостерігати, що за незмінного обсягу капіталу, з кожною додатково використаною одиницею ресурсу "праця", зростає обсяг випуску. Разом з тим, динаміка кожного рядка показує, що кожна наступна одиниця праці (за незмінного обсягу капіталу) забезпечує менший приріст загального обсягу випуску.
Рухаючись згори донизу по кожному зі стовпчиків, ми спостерігаємо динаміку загального випуску, за незмінного обсягу ресурсу "праця", при зміні обсягу капіталу на одну одиницю. Тут теж чітко простежується дія закону спадної продуктивності при змінному ресурсі "праця".
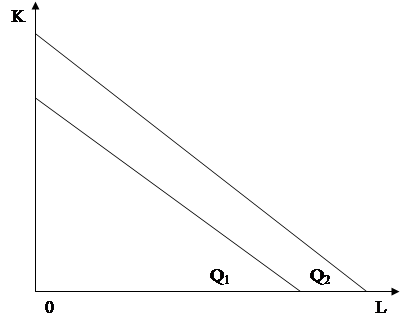
Зобразимо графічно вплив змін у затратах праці та капіталу на загальний обсяг випуску за допомогою ізоквант (рис. 1.2).
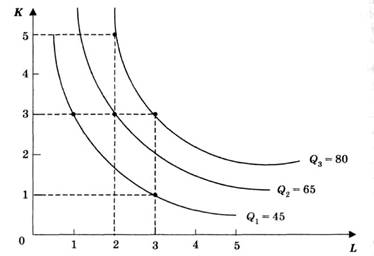
Рис. 1.2 Обсяги випуску за різних комбінацій двох змінних ресурсів.
Ізокванта — це крива, що показує різні комбінації змінних ресурсів, що забезпечують однаковий випуск продукції.
На рис. 1.2 зображено три ізокванти, побудованих за даними табл. 1.1. Наприклад, ізокванта Q показує всі можливі комбінації ресурсів праці та капіталу, що забезпечують максимальний обсяг випуску 45 од. Ізокванта Q2 зміщена праворуч вгору від ізокванти Q1 Це означає, що будь-яка комбінація ресурсів на цій кривій забезпечує більший, (ніж на кривій Q1), обсяг випуску (Q2= 65 од). Ізокванта Q3 показує різні комбінації ресурсів, що забезпечують максимальний обсяг випуску 80 од.
Карта ізоквант — це набір ізоквант, кожна із яких показує максимально можливий обсяг випуску за різних комбінацій ресурсів. Вона є альтернативними способом опису виробничої функції, подібно до того, як карта кривих байдужості є альтернативним описом функції корисності.
Ізокванти демонструють наявність багатоваріантності при прийнятті виробничих рішень керівництвом фірми. Можна домогтися певного обсягу випуску продукції, використовуючи різні поєднання виробничих факторів. Ізокванти звичайно вказують на існування багатьох альтернативних можливостей для забезпечення певного обсягу продукції при різних співвідношеннях між факторами виробництва. Ця обставина має надзвичайно важливе значення для підприємств, оскільки вони вишукують такі співвідношення, які забезпечують мінімальні витрати виробництва.
При аналізі ізоквант можна обмежитись ефективними комбінаціями факторів на ізокванті, оскільки заміщуваність доцільна лише тоді, коли за допомогою збільшення затрат одного фактора забезпечується зниження затрат іншого фактора. Якщо при виробництві визначеного обсягу продукції збільшення затрат одних факторів не супроводжується зменшенням затрат хоча б одного іншого фактора, то такий процес суперечить принципу ефективності.
Чим далі від початку координат розміщена ізокванта, тим більший обсяг випуску забезпечують різні комбінації ресурсів на ній.
Варто зауважити, що лише двофакторна виробнича функція (праця і капітал) дає можливість графічного аналізу виробництва. Якщо ж ураховувати більше факторів, то необхідно застосовувати математичний аналіз.
Отже, ми розглянули виробничу функцію за умови, що обидва ресурси є змінними. У зв'язку з цим виникає питання про доцільність (чи недоцільність) заміни одного ресурсу іншим.
Гранична норма технологічного заміщення (МRTS, від англ. marginal of technical substitution) — це величина, на яку можна зменшити обсяг одного ресурсу за рахунок використання додаткової одиниці іншого ресурсу за незмінного обсягу випуску.
Граничну норму заміщення капіталу працею математично можна подати у вигляді формули:
МRTSKL = – ΔK / ΔL = – dK / dL(1.6)
де ΔK та ΔL – малі обсяги зміни капіталу і праці за ізоквантою при Q = const
У формулі (1.6) капітал заміщується працею. Якщо ж є потреба в тому, щоб працю замістити капіталом, формула МRTS матиме зворотний вигляд:
МRTSKL = – ΔL / ΔK = – dL / dK(1.7)
Оскільки співвідношення зміни обсягу праці та обсягу капіталу — величини від'ємні, то гранична норма заміщення праці капіталом чи капіталу працею має бути величиною додатною.
Економічний зміст того, що МRTS — величина додатна полягає в тому, що якщо капітал заміщується працею і МRTS = 10, то це означає, що з кожною одиницею приросту ресурсу "праця" обсяг капіталу зменшується на 10 одиниць.
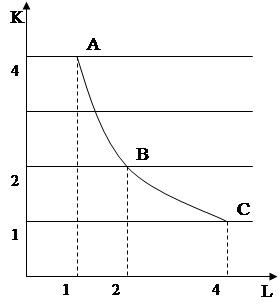
Розглянемо графічну інтерпретацію МRTS (рис. 1.3). Для цього скористаємось однією (середньою) ізоквантою, зображеною на рис. 1.3.
Як видно із рис. 1.3, рухаючись по ізокванті Q2 = 65, МRTSКL зменшується від 1 до 1/2 .
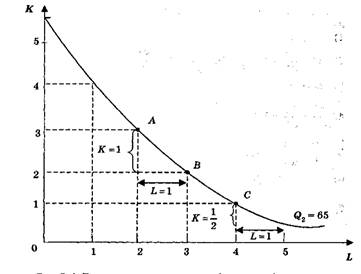
Рис. 1.3 Гранична норма технологічного заміщення
Із формули МRTSКL = MPL / MPK випливає, що рухаючись вздовж ізокванти, безперервне заміщення капіталу працею зумовлює зростання граничного продукту капіталу та зменшення граничного продукту праці. Внаслідок цих змін МRTS зменшується, а ізокванта стає пологішою.
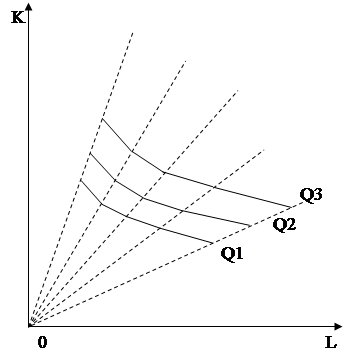
Конфігурація ізоквант залежить від ступеня взаємозамінності чи взаємодоповнюваності ресурсів, про що свідчать графічні зображення на рис. 1.4.
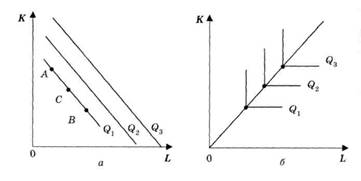
Рис. 1.4 а,б Конфігурація ізоквант.
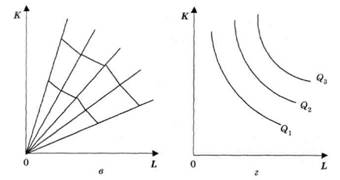
Рис. 1.4 в,г Конфігурація ізоквант.
Пояснення до рисунку 1.4: а — ресурси абсолютно взаємозамінні, MRTS = const у будь-якій точці ізокванти; у точці А обсяг випуску Q1 досягається переважно за рахунок капіталу; в точці В — в основному за рахунок праці; у точці С — за рахунок поєднання капіталу і праці. Приклад використання такої функції продаж білетів у метрополітені автоматами та вручну касирами; б — функція має сталі (незмінні) пропорції між працею і капіталом; ні окреме зростання праці, ні окреме зростання капіталу не можуть забезпечити збільшення обсягу випуску; ↑Q вимагає водночас зростання в однакових пропорціях L i К. Приклад: лісозаготівля потребує обов'язкового ↑L і ↑K; в — ламана ізокванта передбачає тільки декілька способів виробництва; MRTS, рухаючись по ламаній ізокванті зверху вниз праворуч, спадає. Прикладом використання функції є лінійне програмування.
Більшість інженерів, підприємців та виробників вважають, що ламана ізокванта найбільш реалістично показує виробничі можливості більшості сучасних виробництв; г — постійна, але недосконала взаємозамінність ресурсів; спадна гранична норма заміщення, за певною межею заміщення одного ресурсу іншим стає або технічно неможливим, або неефективним, виробництво потребує збалансування ресурсів. Традиційна економічна теорія звичайно оперує гладкими ізоквантами, подібними зображеній на цьому рисунку, оскільки їх аналіз не вимагає застосування складних математичних методів.
Розділ 2. Дослідження і аналіз застосування виробничої функції
Похожие работы
... ресурсів і незмінній технології. Зміна технології веде до зміни самої функціональної залежності. В залежності від кількості факторів, виробнича функція визначається як однофакторна, двофакторна, багатофакторна. [3, 65] В теорії виробництва традиційно використовується двофакторна виробнича функція. Двофакторна виробнича функція у табличній формі подається у вигляді так званої виробничої сітки ( ...
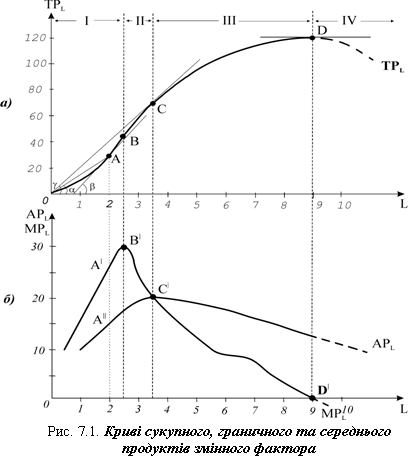
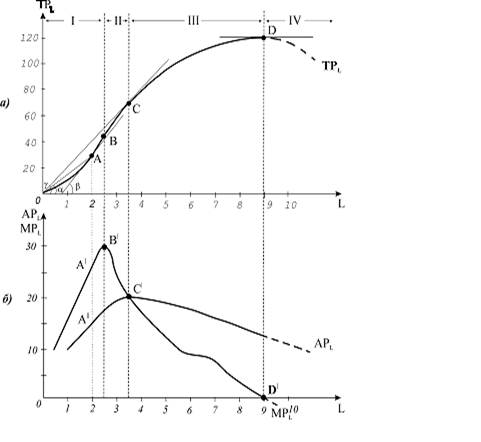
... продуктивність змінного фактора – це кількість продукції, виробленої на одиницю затрат змінного фактора: . Припустимо, що фірма нарощує обсяги виробництва , збільшуючи лише кількість праці , яка є єдиним змінним фактором, за незмінних обсягів капіталу (рис. 7.1). Якщо кількість змінного фактора дорівнює нулю, то обсяг продукції також дорівнює нулю. В міру залучення у виробництво все більшого ...
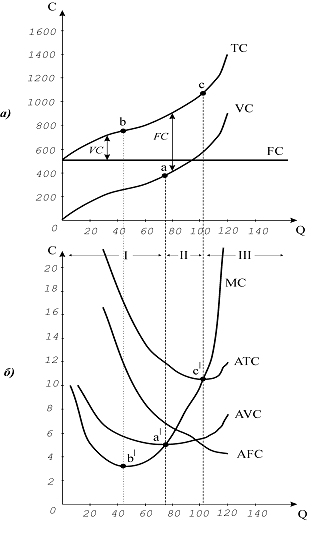
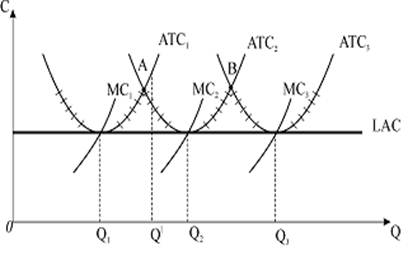
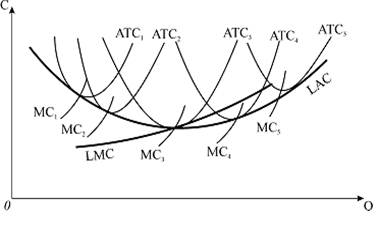
... збитки і буде витіснена з ринку, тому мінімізація середніх витрат складає основне завдання виробничої діяльності фірми. Між середніми сукупними витратами короткострокового і довгострокового періоду існує певний зв’язок. Крива довгострокових середніх витрат будується на основі кривих короткострокових середніх сукупних витрат. Відображаючи дію закону спадної віддачі, короткострокові мають U – поді ...
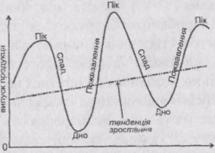
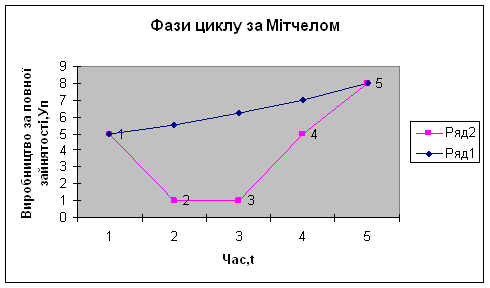
... які виробляють засоби виробництва і споживчі товари тривалого вжитку. У галузях, які випускають споживчі товари короткострокового використання, коливання зайнятості і випуску є значно меншими. 2.2 Фази циклу за Мітчелом Для ринкової економіки характерна макроекономічна нестабільність: економіка розвивається циклічно, виникає безробіття, відбувається інфляція. Поняття «нестабільність» означа ...

0 комментариев