Навигация
Генерування істинних похибок для дослідження математичної моделі методом статистичних випробувань Монте Карло
2. Генерування істинних похибок для дослідження математичної моделі методом статистичних випробувань Монте Карло
По шкалі Спірбергера [1] незалежні змінні представляються з точністю 0,1. прийнято, що точність спостережень дорівнює половині шкали.
Тому логічно генерувати випадкові похибки з точністю, яка б дорівнювала 0,05, тобто половині шкали з якою ми працюємо. Але поставимо перед собою задачу ще дослідити математичні моделі з граничною точністю, яку приймемо вдвічі більшу за 0,05, тобто рівну 0,1. При цьому непарні моделі генерують середню квадратичну похибку 0,1, а парні – 0,05.
Сучасні калькулятори мають “вшиті” генератори для генерування випадкових чисел від 0 до 1. але вони генерують числа тільки зі знаком “плюс”.
Приведемо методику розрахунку випадкових чисел, які приймемо в подальшому як істинні похибки для побудови спотвореної моделі.
1. Отримавши ряд випадкових (а точніше псевдовипадкових) чисел ξі , натиском клавіш К, Cч, розраховують середнє арифметичне генерованих псевдовипадкових чисел ξір .
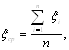 (2.1)
(2.1)
де п – сума випадкових чисел.
2. Розраховуються попередні значення істинних похибок Δ΄і за формулою
![]() , (2.2)
, (2.2)
3. Знаходять середню квадратичну похибку попередніх істинних похибок за формулою Гаусса
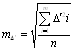
![]() , (2.3)
, (2.3)
4. Вичисляють коефіцієнт пропорційності К для визначення істинних похибок необхідної точності
![]() , (2.4)
, (2.4)
де С – необхідна нормована константа.
Так, наприклад, при т Δ΄ = 0,28 і необхідності побудови математичної моделі з точністю с=0,1, будемо мати
![]() ,
,
а при С=0,05, отримаємо К0,05= 0,05/0,28 =0,178
5. Істинні похибки розраховуються за формулою
![]() , (2.5)
, (2.5)
6. Заключним контролем служить розрахунок середньої квадратичної похибки т∆ генерованих істинних похибок ∆
![]() , (2.6)
, (2.6)
і порівняння
![]() (2.7)
(2.7)
Таблиця 2. Генерування псевдовипадкових чисел і розрахунок істинних похибок
| № п/п | ξ і | - ξср |
| ∆΄і2 |
| ∆і2 |
| 1 | 0,008 | 0,457 | -0,449 | 0,20174 | -0,207 | 0,04283629 |
| 2 | 0,39 | 0,457 | -0,067 | 0,004457 | -0,031 | 0,00094637 |
| 3 | 0,37 | 0,457 | -0,087 | 0,007527 | -0,04 | 0,00159833 |
| 4 | 0,78 | 0,457 | 0,3232 | 0,104484 | 0,149 | 0,02218548 |
| 5 | 0,47 | 0,457 | 0,0132 | 0,000175 | 0,0061 | 0,00003722 |
| 6 | 0,24 | 0,457 | -0,217 | 0,046985 | -0,100 | 0,00997656 |
| 7 | 0,46 | 0,457 | 0,0032 | 1,05E-05 | 0,00149 | 0,00000223 |
| 8 | 0,61 | 0,457 | 0,1532 | 0,023482 | 0,071 | 0,00498610 |
| 9 | 0,5 | 0,457 | 0,0432 | 0,00187 | 0,01992 | 0,00039699 |
| 10 | 0,74 | 0,457 | 0,2832 | 0,080225 | 0,13052 | 0,01703443 |
| П = 10 | 4,568 | Суми | 8E-16 | 0,470955 | 3,6E-16 | 0,10000000 |
Середня квадратична похибка попередніх істинних похибок
mΔ’![]() = (0,470955/10)0.5 =0,2170151.
= (0,470955/10)0.5 =0,2170151.
Коефіцієнт пропорційності
![]() .
.
Середня квадратична похибка при генеруванні випадкових чисел з точністю с=0,1
mΔ’ =(0.10000000/10)0.5 = 0.1000000.
Таблиця 3. Побудова спотвореної моделі
| № п/п | Істинна Хіст. | Модель Уіст. | ∆іст. | Хспотв. |
| 1 | 1,6 | 18,021 | -0,207 | 1,393 |
| 2 | 2 | 13,864 | -0,031 | 1,969 |
| 3 | 2,1 | 13,167 | -0,04 | 2,060 |
| 4 | 2,3 | 11,986 | 0,149 | 2,449 |
| 5 | 2,5 | 10,898 | 0,0061 | 2,506 |
| 6 | 2,8 | 8,949 | -0,100 | 2,700 |
| 7 | 2,9 | 8,101 | 0,00149 | 2,901 |
| 8 | 3 | 7,108 | 0,071 | 3,071 |
| 9 | 3,1 | 5,939 | 0,01992 | 3,120 |
| 10 | 3,3 | 2,965 | 0,13052 | 3,431 |
| п = 10 | 25,6 | 100,998 | 3,6E-16 | 25,600 |
По даним спотвореної моделі виконують строге зрівноваження методом найменших квадратів і отримують ймовірніші моделі, яким роблять оцінку точності зрівноважених елементів і дають порівняльний аналіз на основі якого заключають на предмет поширення даної моделі для рішення проблеми в цілому.
0 комментариев