Навигация
Оцінка точності параметрів, отриманих із рішення системи нормальних рівнянь
7. Оцінка точності параметрів, отриманих із рішення системи нормальних рівнянь
Середні квадратичні похибки визначаємих невідомих х1, х2, х3, х4 , розраховуються за формулами![]() , (7.1.)
, (7.1.)
![]() , (7.2)
, (7.2)
![]() , (7.3)
, (7.3)
![]() , (7.4)
, (7.4)
де тх1 , тх2 , тх3 , тх4 –середні квадратичні похибки невідомих, що визначаємо х1, х2, х3, х4 , т – середня квадратична похибка одиниці ваги, яка розраховується за формулою
![]() , (7.5)
, (7.5)
У формулі (7.5) п – число значень факторних і результуючих ознак (х і у), к – степінь поліному. В нашому випадку п=10; к=3. V- різниця між вихідним значенням уі і вирахуваним значенням у΄ за отриманою нами формулою (5.17);
![]() , (7.6)
, (7.6)
А11 , А22 , А33 , А44 – алгебраїчні доповнення першого, другого, третього і четвертого діагональних елементів
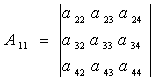 , (7.7)
, (7.7)
 , (7.8)
, (7.8)
 , (7.9)
, (7.9)
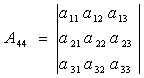 , (7.10)
, (7.10)
де
![]() (7.11)
(7.11)
Приведемо формулу розкриття визначника третього порядку
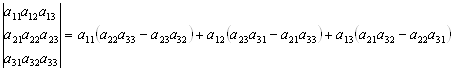 . (7.12)
. (7.12)
І в нашому випадку отримаємо
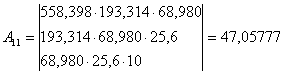
Величина оберненої ваги
![]() (1/Px11)0.5= 10.399008.
(1/Px11)0.5= 10.399008.
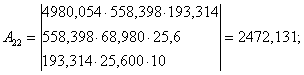
![]() (1/Px2)0.2= 71,748385.
(1/Px2)0.2= 71,748385.
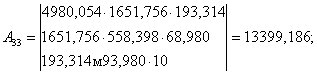
![]() ; (1/Px33)0.5=843.11354
; (1/Px33)0.5=843.11354
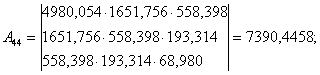
![]() ; (1/Px44)0.5 = 256.49004.
; (1/Px44)0.5 = 256.49004.
Підставляючи у виведену нами формулу (5.17) значення Х спотвореної моделі, отримаємо розрахункові значення у΄, які будуть дещо відрізнятись від вихідних значень У.
Таблиця 6. Порівняльний аналіз результатів строгого зрівноваження.
| № п/п | Хвихідне | Увихідне | У΄зрівноваж.. | V=Уі - Уі΄ | V2 |
| 1 | 1,6 | 18,021 | 17,974 | 0,04708 | 0,00222 |
| 2 | 2 | 13,864 | 13,956 | -0,0918 | 0,00843 |
| 3 | 2,1 | 13,167 | 13,426 | -0,2586 | 0,06686 |
| 4 | 2,3 | 11,986 | 11,186 | 0,80025 | 0,6404 |
| 5 | 2,5 | 10,898 | 10,841 | 0,05685 | 0,00323 |
| 6 | 2,8 | 8,949 | 9,5967 | -0,6477 | 0,41946 |
| 7 | 2,9 | 8,101 | 8,1308 | -0,0298 | 0,00089 |
| 8 | 3 | 7,108 | 6,7115 | 0,39646 | 0,15718 |
| 9 | 3,1 | 5,939 | 6,2588 | -0,3198 | 0,10227 |
| 10 | 3,3 | 2,965 | 2,918 | 0,047 | 0,00221 |
| п=10 | 25,6 | 100,998 | 101,00 | 0,000 | 1,403 |
Тоді, середня квадратична похибка одиниці ваги буде
![]()
Середня квадратична похибка визначення коефіцієнта а
![]()
Середня квадратична похибка визначення коефіцієнта b
![]()
Середня квадратична похибка визначення коефіцієнта с
![]()
Середня квадратична похибка визначення коефіцієнта d
![]()
Висновки.
На основі проведених досліджень в даній роботі:
1. Генеровані випадкові числа, які приведено до нормованої досліджуваної точності.
2. На основі істинної моделі і генерованих істинних похибок побудована спотворена модель впливу ситуативної тривожності на характеристики пам’яті.
3. Математична модель апроксимована по способу найменших квадратів кубічним поліномом.
4. Отримана формула
![]() залежності характеристик пам’яті У від ситуативної тривожності Х.
залежності характеристик пам’яті У від ситуативної тривожності Х.
5. Встановлено, що середня квадратична похибка одиниці ваги за результатами зрівноваження складає ![]() балів по шкалі Спірбергера:
балів по шкалі Спірбергера:
середня квадратична похибка визначення коефіцієнта а при х3 та= 0,676073 ;
середня квадратична похибка визначення коефіцієнта b при х2 тb= 4,900198 ;
середня квадратична похибка визначення коефіцієнта с при х тс= 11,4082 ;
середня квадратична похибка визначення коефіцієнта d тd= 8,472532 ;
6. Розроблена методика підготовки істинних похибок наперед заданої точності.
7. Дана робота відкриває дорогу для проведення досліджень методом статистичних випробовувань Монте Карло.
8. Вона дає можливість охопити велику аудиторію, тому що генеруються похибки індивідуально і вони не повторюються в других моделях.
9. Робота виконується вперше. Нам невідомі літературні джерела, де б виконувались аналогічні дослідження в царині психології.
Література.
1. Максименко С.Д., Е.Л. Носенко Експериментальна психологія (дидактичний тезаурус). Навчальний посібник –К.: МАУП, 2004, -128 с.
2. Літнарович Р.М. Основи математики. Дослідження впливу ситуативної тривожності на характеристики пам’яті. Навчальний посібник для студентів Педагогічного факультету. Частина 2. МЕГУ, Рівне, 2006,-270.
3. Літнарович Р.М. Основи математики. Дослідження результатів психолого-педагогічного експерименту логарифмічною функцією. Частина 3. МЕГУ, Рівне, 2006 –19с.
4. Літнарович Р.М. Основи математики. Дослідження результатів психолого-педагогічного експерименту експоненціальною функцією. Частина 4. МЕГУ, Рівне, 2006 –17с.
5. Літнарович Р.М. Основи математики. Дослідження результатів психолого-педагогічного експерименту степенною функцією. Частина 5. МЕГУ, Рівне, 2006, - 17с.
6. Літнарович Р.М. Дослідження точності апроксимації результатів психолого-педагогічного експерименту методом статистичних випробувань Монте Карло.Ч.1.МЕГУ, Рівне,2006,-45с.
Додаток 1
Генерування псевдовипадкових чисел, підпорядкування їх нормальному закону розподілу і розрахунок істинних похибок
| 0,008 | 0,457 | -0,449 | 0,20174 | -0,207 | 0,04283629 |
| 0,39 | 0,457 | -0,067 | 0,004457 | -0,031 | 0,00094637 |
| 0,37 | 0,457 | -0,087 | 0,007527 | -0,04 | 0,00159833 |
| 0,78 | 0,457 | 0,3232 | 0,104484 | 0,149 | 0,02218548 |
| 0,47 | 0,457 | 0,0132 | 0,000175 | 0,0061 | 0,00003722 |
| 0,24 | 0,457 | -0,217 | 0,046985 | -0,100 | 0,00997656 |
| 0,46 | 0,457 | 0,0032 | 1,05E-05 | 0,00149 | 0,00000223 |
| 0,61 | 0,457 | 0,1532 | 0,023482 | 0,071 | 0,00498610 |
| 0,5 | 0,457 | 0,0432 | 0,00187 | 0,01992 | 0,00039699 |
| 0,74 | 0,457 | 0,2832 | 0,080225 | 0,13052 | 0,01703443 |
| 4,568 | Суми | 8E-16 | 0,470955 | 3,6E-16 | 0,10000000 |
| A | B | C | D | E | F |
Додаток 2.Побудова спотвореної моделі
| 1,393 | 1,6 | 18,021 | -0,207 | 1,393 |
| 1,969 | 2 | 13,864 | -0,031 | 1,969 |
| 2,060 | 2,1 | 13,167 | -0,04 | 2,060 |
| 2,449 | 2,3 | 11,986 | 0,149 | 2,449 |
| 2,506 | 2,5 | 10,898 | 0,0061 | 2,506 |
| 2,700 | 2,8 | 8,949 | -0,100 | 2,700 |
| 2,901 | 2,9 | 8,101 | 0,00149 | 2,901 |
| 3,071 | 3 | 7,108 | 0,071 | 3,071 |
| 3,120 | 3,1 | 5,939 | 0,01992 | 3,120 |
| 3,431 | 3,3 | 2,965 | 0,13052 | 3,431 |
| 25,600 | 25,6 | 100,998 | 3,6E-16 | 25,600 |
| I | G | H | E | I |
|
|
|
|
|
|
| Хспотв. | Xіст. | Уіст. | Істинні похиб. | Хспотв. |
Додаток 3.Розрахункова таблиця
| 1 | 1,941 | 2,703 | 3,766 | 5,246 | 7,307 | 25,10381 | 34,97037 |
| 1 | 3,878 | 7,636 | 15,038 | 29,614 | 58,316 | 27,3015 | 53,76312 |
| 1 | 4,244 | 8,742 | 18,009 | 37,099 | 76,424 | 27,1243 | 55,87662 |
| 1 | 5,997 | 14,687 | 35,968 | 88,084 | 215,713 | 29,35309 | 71,88419 |
| 1 | 6,281 | 15,740 | 39,445 | 98,854 | 247,737 | 27,31149 | 68,44533 |
| 1 | 7,291 | 19,686 | 53,153 | 143,520 | 387,521 | 24,16335 | 65,24388 |
| 1 | 8,419 | 24,427 | 70,874 | 205,640 | 596,663 | 23,50499 | 68,19956 |
| 1 | 9,429 | 28,952 | 88,900 | 272,976 | 838,204 | 21,82591 | 67,01892 |
| 1 | 9,734 | 30,369 | 94,749 | 295,611 | 922,284 | 18,52923 | 57,80981 |
| 1 | 11,768 | 40,372 | 138,496 | 475,113 | 1629,884 | 10,17148 | 34,89342 |
| 10 | 68,980 | 193,314 | 558,398 | 1651,756 | 4980,054 | 234,389 | 578,105 |
| J | K | L | M | N | O | P | Q |
| X0 | X^2 | X^3 | X^4 | X^5 | X^6 | YX | YX^2 |
Продовження розрахункової таблиці
| 48,7148 | 17,974 | 0,04708 | 0,00222 | 324,7564 |
| 105,8723 | 13,956 | -0,0918 | 0,00843 | 192,2105 |
| 115,107 | 13,426 | -0,2586 | 0,06686 | 173,3699 |
| 176,0406 | 11,186 | 0,80025 | 0,6404 | 143,6642 |
| 171,5309 | 10,841 | 0,05685 | 0,00323 | 118,7664 |
| 176,1661 | 9,5967 | -0,6477 | 0,41946 | 80,0846 |
| 197,8805 | 8,1308 | -0,0298 | 0,00089 | 65,6262 |
| 205,7891 | 6,7115 | 0,39646 | 0,15718 | 50,52366 |
| 180,3622 | 6,2588 | -0,3198 | 0,10227 | 35,27172 |
| 119,7025 | 2,918 | 0,047 | 0,00221 | 8,791225 |
| 1497,166 | 101,00 | 0,000 | 1,403 | 1193,065 |
| R | S | T | U | V |
| YX^3 | Yзрівн. | V=Yi-Yз | VV | YY |
Додаток 5. Розрахунок визначників
| 4980,054 | 1651,756 | 558,398 | 193,314 |
| 1651,756 | 558,398 | 193,314 | 68,980 |
| 558,398 | 193,314 | 68,980 | 25,6 |
| 193,314 | 68,980 | 25,6 | 10 |
| D= | 20,637181 | ||
| 1497,166 | 1651,756 | 558,398 | 193,314 |
| 578,105 | 558,398 | 193,314 | 68,980 |
| 234,389 | 193,314 | 68,980 | 25,600 |
| 100,998 | 68,980 | 25,600 | 10 |
| D1= | -29,85928 | ||
| 4980,054 | 1497,166 | 558,398 | 193,314 |
| 1651,756 | 578,105 | 193,314 | 68,980 |
| 558,398 | 234,389 | 68,980 | 25,6 |
| 193,314 | 100,998 | 25,6 | 10 |
| D2= | 196,95168 | ||
| 4980,054 | 1651,756 | 1497,166 | 193,314 |
| 1651,756 | 558,398 | 578,105 | 68,980 |
| 558,398 | 193,314 | 234,389 | 25,6 |
| 193,314 | 68,980 | 100,998 | 10 |
| D3= | -550,4712 | ||
| 4980,054 | 1651,756 | 558,398 | 1497,166 |
| 1651,756 | 558,398 | 193,314 | 578,105 |
| 558,398 | 193,314 | 68,980 | 234,389 |
| 193,314 | 68,980 | 25,6 | 100,998 |
| D4= | 836,2791 | ||
Додаток 6.Вільні члени нормальних рівнянь
| 1497,166 |
| 578,105 |
| 234,389 |
| 100,998 |
Додаток 7.Розрахунок коефіцієнтів апроксимуючого поліному
| a=D1/D= | -1,446868 |
| b=D2/D= | 9,543536 |
| c=D3/D= | -26,67376 |
| d=D4/D= | 40,522935 |
| Y=aX^3+bX^2+cX+d | |
Нами виведена формула за результатами теоретичних досліджень
![]()
Додаток 8.Знаходження алгебраїчних доповнень
| 4980,054 | 1651,756 | 558,398 | ||||||
| A44= | 7390,4458 | 1651,756 | 558,398 | 193,314 | ||||
| 558,398 | 193,314 | 68,980 | ||||||
| 4980,054 | 558,398 | 193,314 | ||||||
| A22= | 2472,131 | 558,398 | 68,980 | 25,6 | ||||
| 193,314 | 25,600 | 10 | ||||||
| A33= | 13399,186 | 4980,054 | 1651,756 | 193,314 | ||||
| 1651,756 | 558,398 | 68,980 | ||||||
| 193,314 | 68,980 | 10 | ||||||
| 558,398 | 193,314 | 68,980 | ||||||
| A11= | 47,05777 | 193,314 | 68,980 | 25,6 | ||||
| 68,980 | 25,6 | 10 | ||||||
| Додаток | 9. | |||||||
| КОНТРОЛЬ ЗРІВНОВАЖЕННЯ: | ||||||||
|
| ||||||||
| 1,40315 | ||||||||
| 1,403150 | ||||||||
| 0,000000 | ||||||||
Додаток 10.Оцінка точності зрівноважених елементів
| Середня | квадратична похибка одиниці ваги | |||
| m= | 0,447716 | |||
| Середня | квадратична похибка коефіцієнта а | |||
| ma= | 0,676073 | |||
| Се редня квадратична похибка коефіцієнта в | ||||
| mb= | 4,900198 | |||
| Середня квадратична похибка коефіцієнта с | ||||
| mc= | 11,4082 | |||
| Середня квадратична похибка коефіцієнта d | ||||
| md= | 8,472532 | |||
Абрамович К.П.
Дослідження точності впливу ситуативної тривожності на характеристики пам’яті методом статистичних випробувань Монте Карло
Модель ППП 051- 1
Комп’ютерний набір, Верстка і макетування та дизайн в редакторі Microsoft®Office® Word 2003 Абрамович Катерина
Міжнародний Економіко-Гуманітарний Університет ім.акад. С.Дем’янчука
Кафедра математичного моделювання
33027,м.Рівне,вул..акад. С.Дем’янчука,4.
0 комментариев