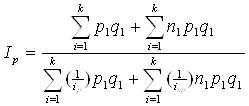
Навигация
Найдем коэффициент вариации:
V=![]()
Вывод: Средний размер семьи равен 5 чел. Коэффициент вариации равен 40%, значит, колеблемость между признаками высокая. Мода и медиана равны, следовательно, ряд является семетричным.
Задача 6. Используя приведённые данные о количестве и затратах труда на производство продукции, сделайте факторный анализ производительности труда.
| Вид продукции | Количество продукции | Прямые затраты труда на производство ед. продукции, в человеко-часах | Сопоставимые цены, руб. | ||
| Базисный год | Отчётный год | Базисный год | Отчётный год | ||
| символы | q0 | q1 | t0 | t1 | p |
| А | 320 | 345 | 48,4 | 40,9 | 200 |
| Б | 900 | 1300 | 13,0 | 15,0 | 80 |
| В | 16000 | 14800 | 5,0 | 3,0 | 40 |
Решение:
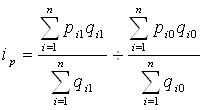
1.Найдем общий индекс:
![]()
Индекс производительности труда уменьшился на 27%.
2.Найдем как количество продукции влияет на индекс производительности труд.
![]()
Из-за изменения количества продукции производительности труда уменьшится на 31% или 74588 –107188 = –32600 руб.
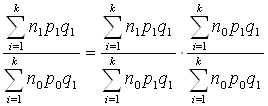
3.Найдем как прямые затраты труда влияют на его производительность.
![]()
Индекс производительности труда увеличился за счёт изменения затрат на 0,3% или на 107598 – 107188 =410 руб.
Задача 7.
Определить по данным предприятиям списочный и среднесписочный состав работающих на начало и конец октября, в среднем за месяц.
На начало октября на предприятии постоянно работали 180 человек.
Кроме того:
– в командировке 2
– в очередном отпуске 7
– в отпуске по уходу за ребёнком 2
– на больничном до 10 дней 5
Движение работников в течение месяца характеризуется следующими данными:
| Число месяца | Изменение численности | Количество рабочих |
| 03.10 | Выбыли в командировку | 4 |
| 05.10 | Приняты на временную работу | 2 |
| 09.10 | Приступили к работе после очередного отпуска | 5 |
| 14.10 | Приняты на постоянную работу | 3 |
| 22.10 | Уволены за прогул | 4 |
| 25.10 | Выбыли в связи с уходом на пенсию | 2 |
| 27.10 | Выбыли по собственному желанию | 2 |
| 30.10 | Приступили к работе после болезни | 5 |
Решение:
Списочный состав работающих на начало октября (ССнач.) =180чел.;
Среднесписочный состав работающих на начало октября (СрСнач.) =
= ССнач. – в командировке – в очередном отпуске – в отпуске по уходу за ребенком – на больничном до 10 дней. СрСнач. = 184–2–7–2–5 = 164 чел.
Списочный состав работающих на конец октября (ССкон.) =
ССнач. – уволены за прогулы – выбыли в связи с уходом на пенсию – выбыли по собственному желанию + приняты на постоянную работу + принятые на временную работу. ССкон. =180–4–2–2+3+2 = 177 чел.
Среднесписочный состав работающих на конец октября (СрСкон.) =
= ССкон. – в командировке(4+2) – в очередном отпуске (7–5) – в отпуске по уходу за ребенком. СрСкон. =177–6–2–2 = 167 чел.
Задача 8. Менеджер компании, занимающейся прокатом автомобилей, хочет оценить среднюю величину пробега одного автомобиля в течение месяца. Из 280 автомобилей, принадлежащих компании, методом случайной бесповторной выборки отобрано 30. По данным этой выборки установлено, что средний пробег автомобиля в течение месяца составляет 1342 км. со стандартным отклонением 227 км. Считая пробег автомобиля случайной величиной, распределённой по нормальному закону, найдите 95%-ный доверительный интервал, оценивающий средний пробег автомобилей всего парка в течение месяца.
Решение:
(Средний пробег автомобилей всего парка) 95% =0,954;
t (0,954) =2(коэффициент доверия)
![]() = 227 км
= 227 км
n = 30 шт.
N = 280 шт.
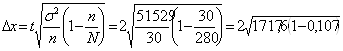 =
=![]() км
км
Найдем интервал, оценивающий средний пробег автомобилей всего парка в течение месяца (![]() ).
).
1342 км ![]() 78,3 км
78,3 км
Интервал: ![]() км
км
Вывод: В 95% средний пробег автомобиля не выйдет за предел диапазона ![]() км.
км.
Задача 9. Среднемесячный бюджет студентов в колледжах одного из штатов США оценивается по случайной выборке. С вероятностью 0,954 найдите наименьший объём выборки, необходимой для такой оценки, если среднее квадратическое отклонение предлагается равным 100 у.е., а предельная ошибка средней не должна превышать 20 у.е.
Решение:
t (0,954)=2
![]() =100 у.е
=100 у.е
![]() =20 y.e.
=20 y.e.
Найдем наименьший объем выборки:
![]() 1000 у.е.
1000 у.е.![]()
Вывод: Наименьший объем выборки с вероятностью 0,954 составляет 1000 у.е.
Задача 10. Организация стран-экспортёров нефти предпринимает попытки контроля над ценами на сырую нефть с 1973 г. Цены на сырую нефть резко возрастали с середины 70-х до середины 80-х гг., что повлекло за собой некоторое повышение цен на бензин.
| год | Бензин, центов за галлон | Сырая нефть, долл. За баррель |
| 1980 | 119 | 21,59 |
| 1981 | 133 | 31,77 |
| 1982 | 122 | 28,52 |
| 1983 | 116 | 26,19 |
| 1984 | 113 | 25,88 |
| 1985 | 112 | 24,09 |
| 1986 | 86 | 12,51 |
| 1987 | 90 | 15,40 |
| 1988 | 90 | 12,57 |
Постройте график и оцените характер взаимосвязи между переменными. Рассчитайте параметры уравнения регрессии, оценивающего зависимость цен на галлон бензина от цен за баррель нефти. Дайте интерпретацию полученных результатов.
Решение:
Построим поле корреляции и прямую регрессии:
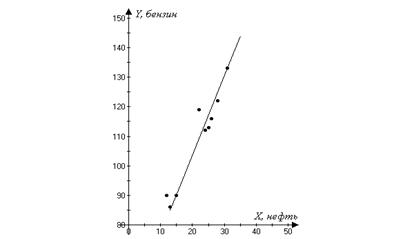
Рис. 3. Поле корреляции и прямая регрессии
![]() - уравнение регрессии
- уравнение регрессии
![]()
| x | y | xy | x2 | yx |
| |||||
| 21,59 31,77 28,52 26,19 25,88 24,09 12,51 15,40 12,57 | 119 133 122 116 113 112 86 90 90 | 2569,21 4225,41 3479,44 3038,04 2924,44 2698,08 1075,86 1386 1131,3 | 466,13 1009,33 813,39 685,92 669,77 580,33 156,50 237,16 158 | 107,97 130,50 123,26 118,06 117,37 113,38 87,55 94,16 87,69 |
| |||||
|
| 198,52 | 981 | 22527,78 | 4776,54 |
| |||||
![]() долл.
долл.
![]() цент.
цент.
![]()
![]() долл.
долл.
![]() ;
;
![]() .
.
Вывод: Связь между бензином и нефтью функциональная. Таким образом, с увеличение цены нефти на 1 долл. цена бензина за галлон увеличилась на 2 цента.
Задача 11. Исследуйте связь между успеваемостью студентов-заочников вуза и работой их по специальности. Результаты характеризуются следующими данными:
| Число студентов | Из них | ||
| Получившие положительные оценки | Получившие неудовлетворительные оценки | ||
| Работающие по специальности | 201 | 184 | 17 |
| Не работающие по специальности | 102 | 37 | 65 |
| Итого | 303 | 221 | 82 |
Решение:
| Число студентов | Из них | ||
| Получившие положительные оценки | Получившие неудовлетворительные оценки | ||
| Работающие по специальности | 69,3% | 83,2% | 20,7% |
| Не работающие по специальности | 33,7% | 16,8% | 79,3% |
| итого | 100% | 100% | 100% |
![]() – студенты, работающие по специальности;
– студенты, работающие по специальности;
![]() – студенты, работающие не по специальности;
– студенты, работающие не по специальности;
![]() – работающие по специальности получили полож. оценки;
– работающие по специальности получили полож. оценки;
![]() – работающие по специальности получили неудовл. оценки;
– работающие по специальности получили неудовл. оценки;
![]() – не работающие по специальности получили полож. оценки;
– не работающие по специальности получили полож. оценки;
![]() – не работающие по специальности получили неуд. оценки.
– не работающие по специальности получили неуд. оценки.
Вывод: Работа по специальности влияет на успеваемость, так как студентов, получивших положительные оценки и работающих по специальности в 5 раз больше, чем студентов, работающих не по специальности и получивших положительную оценку.
Задача 12. Имеются следующие данные по предприятию за год:
1.Среднесписочное число работников, всего, чел. 1000
в том числе:
с продолжительностью рабочего дня 8,0 часов 950
с продолжительностью рабочего дня 7,0 часов
(рабочих горячих цехов) 50
2.Отработано работниками, человеко-дней 214 200
3.Целодневные простои, человеко-дней 40
4.Неявки на работу, человеко-дней 150 760
в том числе:
ежегодные отпуска 22 000
праздничные и выходные дни, человеко-дней 113 000
Определить:
1. Календарный фонд рабочего времени
2. Максимально возможный фонд рабочего времени
3. Коэффициент использования календарного фонда времени
4. Коэффициент использования максимально возможного фонда времени
5. Описать полученные результаты.
Решение:
1.Найдем календарный фонд рабочего времени:
КФРВ=ССЧ![]() 365(366)=1000
365(366)=1000![]() 365=365000 человеко-дней;
365=365000 человеко-дней;
2.Найдем максимально возможный фонд рабочего времени:
МВФРВ=КФРВ – ежегодные отпуска – праздничные и выходные дни = =365000–22000–113000=230000 человеко-дней;
3.Найдем коэффициент использования календарного фонда времени:
КИКФВ = число отработанных человеко-дней / КФРВ = ![]() 0,58 или 58%
0,58 или 58%
Таким образом, 58% затрачено на фактическую работу.
4.Найдем коэффициент использования максимально возможного фонда времени:
КИМВФВ= число отработанных человеко-дней / МВФВ = ![]() 0,93 или 93%
0,93 или 93%
Вывод: КФРВ равен 365000 человеко-дней, МВФРВ равен 230000 человеко-дней, коэффициент использования календарного фонда времени равен 0,58 или 58% и Коэффициент использования максимально возможного фонда времени равен 0,93.
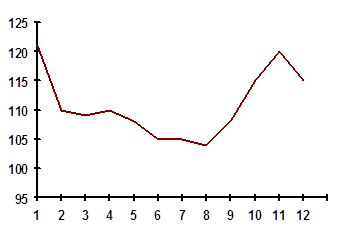
Задача 13. Рассчитать индексы сезонности и построить график сезонной волны по следующим данным о производстве яиц за 3 года:
| Месяц | 1 | 2 | 3 |
| 1 | 10,2 | 9,7 | 11,8 |
| 2 | 15,2 | 16,1 | 14,4 |
| 3 | 17,3 | 14,8 | 15,6 |
| 4 | 19,4 | 22,7 | 16,5 |
| 5 | 21,2 | 25,4 | 29,1 |
| 6 | 26,1 | 28,2 | 25,2 |
| 7 | 28,3 | 25,8 | 23,5 |
| 8 | 21,4 | 23,3 | 23,6 |
| 9 | 22,1 | 20,7 | 18,2 |
| 10 | 14,6 | 15,2 | 16,3 |
| 11 | 9,5 | 8,6 | 13,3 |
| 12 | 12,4 | 12,9 | 14,6 |
Решение:
1.Рассчитаем индексы сезонности.
Найдем сколько в среднем яиц, производилось за 3 года в каждом месяце:
![]() яиц – в январе;
яиц – в январе;
![]() яиц – в феврале;
яиц – в феврале;
![]() яиц – в марте;
яиц – в марте;
![]() яиц – в апреле;
яиц – в апреле;
![]() яиц – в мае;
яиц – в мае;
![]() яиц – в июне;
яиц – в июне;
![]() яиц – в июле;
яиц – в июле;
![]() яиц – в августе;
яиц – в августе;
![]() яиц – в сентябре;
яиц – в сентябре;
![]() яиц – в октябре;
яиц – в октябре;
![]() яиц – в ноябре;
яиц – в ноябре;
![]() яиц – в декабре;
яиц – в декабре;
Найдем среднее значение у:
![]() яиц.
яиц.
Найдем индексы сезонности:
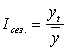
![]() или 57% – производство снизилось в январе на 43%;
или 57% – производство снизилось в январе на 43%;
![]() или 82% – производство снизилось в феврале на 18%;
или 82% – производство снизилось в феврале на 18%;
![]() или 86% – производство снизилось в марте на 14%;
или 86% – производство снизилось в марте на 14%;
![]() или 106% – производство увеличилось в апреле на 6%;
или 106% – производство увеличилось в апреле на 6%;
![]() или 137% – производство увеличилось в мае на 37%;
или 137% – производство увеличилось в мае на 37%;
![]() или 141% – производство увеличилось в июне на 41%;
или 141% – производство увеличилось в июне на 41%;
![]() или 140% – производство увеличилось в июле на 40%;
или 140% – производство увеличилось в июле на 40%;
![]() или 123% – производство увеличилось в августе на 23%;
или 123% – производство увеличилось в августе на 23%;
![]() или 110% – производство увеличилось в сентябре на 10%;
или 110% – производство увеличилось в сентябре на 10%;
![]() или 83% – производство снизилось в октябре на 17%;
или 83% – производство снизилось в октябре на 17%;
![]() или 56% – производство снизилось в ноябре на 44%;
или 56% – производство снизилось в ноябре на 44%;
![]() или 72% – производство снизилось в декабре на28%.
или 72% – производство снизилось в декабре на28%.
2.Построим график сезонной волны:

Рис. 4. График сезонной волны
Вывод: Пик производства яиц за 3 года наблюдается в июне(6), а спад в ноябре месяце (1).
Задача 14. Провести индексный анализ фондоотдачи, фондоёмкости и фондовооружённости по следующим данным:
| Год | Стоимость ОПФ, Тыс. руб. | Стоимость валовой продукции | Среднегодовая численность рабочих, человек |
| 1 | 5700 | 32200 | 414 |
| 2 | 6500 | 29000 | 490 |
Решение:
Фондоотдача – показывает, сколько продукции в стоимостном выражении выпускается на 1 рубль стоимости основных фондов:
![]()
где, Q – объём товаров и услуг выпущенных предприятием в данный период;
Ф – средняя стоимость основных фондов в данном периоде.
Фондоёмкость – характеризует стоимость основных производственных фондов, приходящих на 1 рубль производственных товаров и услуг:
![]()
Фондовооружённость – характеризует, как работники обеспечены основными фондами:
![]()
1.Найдем фондоотдачу:
![]() руб. – за базисный год
руб. – за базисный год
![]() руб. – за отчетный год
руб. – за отчетный год
Найдем индекс фондоотдачи:
![]()
Таким образом, фондоотдача отчетного года уменьшилась по сравнению с базисным годом на 21% или на 1,15 руб.
2.Найдем фондоёмкость:
![]() руб. – за базисный год
руб. – за базисный год
![]() руб. – за отчетный год
руб. – за отчетный год
Найдем индекс фондоёмкости:
![]()
Таким образом, фондоемкость отчетного года увеличилась по сравнению с базисным годом на 22% или на 0,04 руб.
3.Найдем фондовооруженность:
![]() руб. – базисный год
руб. – базисный год
![]() руб. – отчетный год
руб. – отчетный год
Найдем индекс фондовооруженности:
![]()
Таким образом, фондовооруженность отчетного года уменьшилась по сравнению с базисным годом на 24% или на 18,5 руб.
Задача 15. Проанализировать движение основных фондов предприятия (коэффициенты обновления, выбытия, годности) по следующим данным, тыс. руб.:
| Наименование ОС | Наличие на начало года | Поступило за год | Выбыло за год | Наличие на конец года | Амортизация |
| 1. Здания | 9200 | – | 400 | 820 | |
| 2. Сооружения | 2551 | 254 | – | 410 | |
| 3. Машины и оборудование | 3502 | 2305 | 536 | 950 | |
| 4. Транспортные средства | 503 | 116 | 120 | 78 | |
| 5. Инструмент и инвентарь | 168 | 20 | 10 | 15 | |
| 6. Прочие ОС | 55 | – | – | 16 |
Решение:
1.Найдем наличие на конец года всех основных фондов предприятия:
Наличие на конец года всех основных фондов предприятия = =наличие на конец года – выбыло за год + поступило за год;
Найдем наличие на конец года всех фондов предприятия с учетом амортизации:
Наличие на конец года с учетом амортизации = наличие на конец года – амортизация.
| Наименование ОС | Наличие на начало года | Поступило за год | Выбыло за год | Наличие на конец года | Амортизация | Наличие на конец года с учетом амортизации |
| 1. Здания | 9200 | – | 400 | 8800 | 820 | 7980 |
| 2.Сооружения | 2551 | 254 | – | 2805 | 410 | 2395 |
| 3.Машины и оборудование | 3502 | 2305 | 536 | 5271 | 950 | 4321 |
| 4.Транспортные средства | 503 | 116 | 120 | 499 | 78 | 421 |
| 5.Инструмент и инвентарь | 168 | 20 | 10 | 178 | 15 | 163 |
| 6.Прочие ОС | 55 | – | – | – | 16 | – |
2)Найдем:
Коэффициент обновления = поступило за год/ наличие на конец года
Коэффициент выбывания = выбыло за год/ наличие на начало года
Коэффициент годности = годность ОС/ наличие на конец года
| Наименование ОС | Коэффициент обновления | Коэффициент выбывания | Коэффициент годности |
| 1.Здания | – | 0,04 | 0,9 |
| 2.Сооружения | 0,11 | – | 0,85 |
| 3. Машины и оборудование | 0,43 | 0,15 | 0,82 |
| 4. Транспортные средства | 0,23 | 0,24 | 0,84 |
| 5. Инструмент и инвентарь | 0,11 | 0,05 | 0,91 |
Вывод: Наибольшие обновления произошли у машин и оборудования. Наибольший коэффициент выбывания наблюдается у транспортных средств. Наибольший коэффициент годности у основных средств – инструмент и инвентарь.
Задача 16. Ежегодное изменение физического объёма ВВП характеризуется следующим рядом динамики:
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ВВП в % к предыдущему году | 95,0 | 85,5 | 91,3 | 87,3 | 95,9 | 96,6 | 100,9 | 95,5 |
Проанализировать данный ряд с помощью показателей динамики (абсолютных, относительных и средних). Построить график, сделать выводы.
Решение:
1.Найдем показатели динамики:
| Показатели | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Абсолютный прирост | – | –9,5 | 5,8 | –4 | 8,6 | 0,7 | 4,3 | –5,4 | |
| Темп роста | – | 90 | 106 | 95 | 109 | 101 | 104 | 94 | |
| Темп прироста | – | –10 | 6 | –5 | 9 | 1 | 4 | –6 | |
| Средний уровня ряда |
|
| |||||||
| Средний абсолютный прирост |
|
| |||||||
| Средний темп роста |
|
| |||||||
| Средний темп прироста |
темпа прироста не наблюдается |
| |||||||
2.Построим график динамики уровня ряда за период 1 – 8 гг.
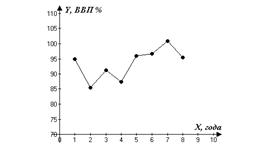
Рис. 5. График динамики уровня ряда
Вывод: В среднем ВВП составляет 93,5%, при этом средний темп роста равен 1,а средний темп прироста не наблюдается. Самый низкий показатель ВВП за 2-ой год, самый высокий за 7-ой год.
Задача 17. Имеются следующие данные о расходе проката чёрных металлов на предприятии:
| Наименование продукции | Произведено за месяц, шт. | Удельный расход проката, кг на ед. продукции | ||
| По норме | Фактически | |||
| Трактор | 500 | 7620 | 7240 | |
| Комбайн | 200 | 2320 | 2300 | |
Определить индексы удельного (на ед.) и общего расхода проката, экономию материалов.
Решение:
1.Определим индексы удельного проката:
![]()
![]()
Таким образом, удельный расход проката уменьшился на 5% или на 380 кг на ед.– для трактора.
![]()
![]()
Таким образом, удельный расход проката уменьшился на 1% или на 20 кг на ед. – для комбайна.
2.Определим индексы общего расхода проката:
![]()
![]()
Таким образом, общий расход проката уменьшился на 5% или на 3620000 – 3810000= –190000 кг на ед.– для трактора.
![]()
![]()
Таким образом, общий расход проката уменьшился на 1% или на 460000 – 464000 = –4000 кг на ед. – для комбайна.
Задача 18. Для определения среднего возраста 1200 студентов факультета необходимо провести выборочное обследование методом случайного бесповторного отбора. Предварительно установлено, что среднее квадратическое отклонение возраста студентов равно 10 годам. Сколько студентов надо обследовать, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года?
Решение:
t(0,954)=2;
N=1200;
![]() 10;
10;
![]() =3.
=3.
![]()
![]() =
=![]() студента.
студента.
Вывод: Надо обследовать 43 студента, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года.
Задача 19. По имеющимся данным рассчитать среднее содержание меди в образцах, моду, медиану, сделать вывод о симметричности распределения.
| Содержание меди, % | Количество образцов |
| 56-58 58-60 60-62 62-64 64-66 66-68 68-70 70-72 72-74 | 5 29 63 116 117 102 48 14 6 |
Решение:
1.Найдем показатели дискретного ряда:
| Содержание меди, % | Количество образцов | Показатели дискретного ряда |
| 56-58 58-60 60-62 62-64 64-66 66-68 68-70 70-72 72-74 | 5 29 63 116 117 102 48 14 6 | 57 59 61 63 65 67 69 71 73 |
![]() =
=![]()
Таким образом, среднее содержание меди в образцах составляет 65%.
2.Найдем моду и медиану:
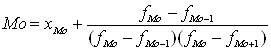
![]()
![]()
![]() =
= 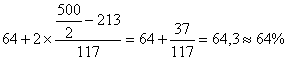
Вывод: Ряд является симметричным, так как мода примерно равна медиане: ![]() ;
; ![]()
Задача 20. С помощью уравнения регрессии спрогнозировать затраты на рубль произведённой продукции при ожидаемой прибыли 800 тыс. руб. по следующим данным:
| Затраты на 1 рубль произведённой продукции, коп. | Прибыль, тыс. руб. |
| 77 77 81 82 89 96 | 1070 1001 789 779 606 221 |
Решение:
Найдем уравнение регрессии:
![]() – уравнение регрессии;
– уравнение регрессии;
x – затраты; y – прибыль.
| x | y | x2 | xy | |||||
| 77 77 81 82 89 96 | 1070 1001 789 779 606 221 | 5929 5929 6561 6724 7921 9216 | 82390 77077 63909 63878 53934 21216 | |||||
|
| 502 | 4466 | 42280 | 362404 |
| |||
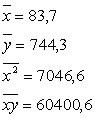
![]()
![]()
![]()
![]()
![]()
![]() коп.
коп.
Вывод: При ожидаемой прибыли 800 тыс. руб. затраты на рубль произведённой продукции равны 82 копейки.
Заключение
Статистика цен образует самостоятельный блок в экономической статистике. Ее показатели помогают исследовать действие рыночного механизма и вместе с тем органично входят в систему показателей уровня жизни, служат в качестве дефляторов любых стоимостных показателей. Анализ цен – важное условие статистического обеспечения ценообразования в экономике.
Основная задача статистики цен – отразить и проанализировать состояние и поведение цен, т. е. их уровень, колеблемость и динамику.
Центральным моментом в анализе цен остается использование индексного метода. В данной курсовой работе проведено изучение различных концепций индексов цен, раскрыта современная методология построения индексов цен, соответствующая международной практике, были показаны преимущества и недостатки индексов Пааше и Ласпейреса и потенциальные возможности других индексных систем.
Кроме того, были рассмотрены задачи и система показателей статистики цен, индексы потребительских цен, индексы цен производства, индексы цен в статистике внешней торговли и решены 20 задач, охватывающие курс статистики.
Таким образом, цели и задачи данной курсовой работы решены.
Литература
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник/ Под ред. чл.-корр. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2001.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. - М.: ИНФРА-М, 1998.
3. Ниворожкина Л.И. и др. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач. – Ростов н/Д: Феникс, 1999.
4. Статистика: Учеб.пособие / Харченко Л.П., и др.;Под ред. канд.экон.наук В.Г.Ионина. – Изд.2-е, перераб. и доп. – М.:ИНФРА-М, 2006. – (Высшее образование).
5. Экономическая статистика: Учебник/ Под ред. Ю.Н. Иванова. - М.: ИНФРА-М, 1999.
Похожие работы
... инфляции около 50%, то имеет место "гиперинфляция". Норма инфляции 10 - 99% характерна для стран с переходной экономикой или для развивающихся стран. 1.3 Система показателей статистики цен Характеристика инфляции тесно связана с анализом ценовой политики. В рыночной экономике одной из важнейших функций цены является балансирующая функция, которая заключается в установлении баланса между ...
... различных товаров. Требования рынка не только расширяют и углубляют задачи статистики цен, вытекающие из плановой концепции, но и принципиально меняют их. В основу современной классификации концептуальных задач статистики цен могут быть положены следующие критерии: цели, достигаемые решением задачи, и субъекты, заинтересованные в решении задачи. Первая классификация включает три концептуальные ...
... , смоделировать и осуществить прогноз изменения цен. Вторая классификация - с позиции пользователей и заказчиков статистической ценовой информации - выделяются следующие общие задачи статистики цен. 1. С позиции государства: изучение цены как орудия социальной и экономической эффективности рынка, как фактора уровня жизни, как главной составляющей инфляционных процессов; изучение влияния цен на ...
... измерить не только относительное изменение отдельных элементов изучаемого явления и явления в целом в текущем периоде по сравнению с базисным, но и абсолютное изменение.[2] 1.3 Понятие о среднеарифметическом и среднегармоническом индексах Индексы количественных показателей. Необходимость в применении особых приемов построения индексов количественных показателей возникает, когда итоги по ...
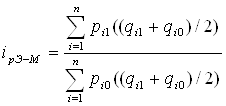
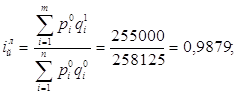
0 комментариев