Матроїди

5. Матроїди

Поняття матроїда тісно пов'язане з поняттям відносини залежності, тому ця тема розглядається в даній кваліфікаційній роботі. Однак з іншої сторони воно є теоретичною основою для вивчення й аналізу «жадібних» алгоритмів.

Визначення 17.

Матроїдом  називається кінцева множина й сімейство його підмножин , таке що виконується три аксіоми:

М₁: ;

М₂: ;

М₃:

 

Визначення 18.

Елементи множини  називаються незалежними, а інші підмножини   - залежними множинами.

Відповідно до уведеного раніше аксіомами простору залежності бачимо, що матроїди - це в точності кінцеві транзитивне простори залежності.

Розглянемо наступні приклади матроїдів:

Приклад 1.

Сімейство всіх лінійно незалежних підмножин будь-якої кінцевої множини векторів довільного непустого векторного простору є матроїдом.

Дійсно, по визначенню можна вважати, що порожня множина лінійно незалежно. Усяка підмножина лінійно незалежної підмножини векторів лінійно незалежно. Нехай  і - лінійно незалежні множини. Якби всі вектори із множини  виражалися у вигляді лінійної комбінації векторів із множини , то множина  була б лінійно залежним. Тому, серед векторів множини  є принаймні один вектор , що не входить у множину  й не виражається у вигляді лінійної комбінації векторів із множини . Додавання вектора  до множини  утворить лінійно незалежна множина.

Приклад 2.

Вільні матроїди. Якщо  - довільна кінцева множина, то  - матроїд. Такий матроїд називається вільним. У вільному матроїді кожна множина незалежно, А є базисом і .

Приклад 3.

Матроїд трансверсалей. Нехай  - деяка кінцева множина, і  - деяке сімейство підмножин цієї множини. Підмножина  називається часткової трансверсалью сімейства , якщо  містить не більш ніж по одному елементі кожної підмножини із сімейства . Часткові трансверсали над  утворять матроїд на А.

Перейдемо до розгляду жадібного алгоритму. Для початку потрібно сформулювати задачу, що будемо вирішувати з його використанням.

Нехай є кінцева множина , , вагова функція  й сімейство .

Розглянемо наступну задачу: знайти , де . Інакше кажучи, необхідно вибрати в зазначеному сімействі підмножина найбільшої ваги.

Не обмежуючи спільності, можна вважати, що

Розглянемо такий алгоритм, що вихідними даними має множину , сімейство його підмножин  і вагарню функцію , причому множина  впорядкована в порядку убування ваг елементів. Після виконання цього алгоритму ми одержимо підмножину .

Споконвічно шукана множина  порожньо, далі переглядаємо по черзі всі елементи із множини  й перевіряємо залежність множини , якщо  - незалежно, те елемент  додаємо в множину , якщо ж  - залежне, те переходимо до елемента , поки всі елементи із множини  не будуть перевірені.

Алгоритм такого типу називається «жадібним». Зовсім очевидно, що по побудові остаточна множина , тобто незалежно. Також очевидно, що жадібний алгоритм є надзвичайно ефективним: кількість кроків становить, тобто жадібний алгоритм є лінійним. (Не вважаючи витрат на сортування множини  й перевірку незалежності .)

Приклад 4.

Нехай дана матриця 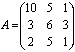. Розглянемо наступні задачі.

Задача 1. Вибрати по одному елементі з кожного стовпця, так щоб їхня сума була максимальна.

Тут вагова функція  ставить у відповідність елементу матриці  його значення. Наприклад, .

Множина  в такий спосіб:

.

Сімейство незалежних підмножин  будуть утворювати такі множини, у яких всі елементи з різних стовпців і порожня множина.

Наш алгоритм буде працювати в такий спосіб:

0 крок: ;

1 крок: перевіряємо для елемента , ;

2 крок: для , ;

3 крок: для , ;

4 крок: для , ;

5 крок: для , ;

6 крок: для , ;

7 крок: для , ;

8 крок: для , ;

9 крок: для , ;

У результаті одержали множину , ., отриманий результат дійсно є рішенням задачі.

Задача 2. Вибрати по одному елементі з кожного рядка, так щоб їхня сума була максимальна.

Тут функція  й множина  такі ж як і в попередній задачі, а сімейство незалежних підмножин  будуть утворювати такі множини, у яких всі елементи з різних рядків і порожня множина.

Використовуючи наш алгоритм одержимо наступне рішення: множина  й , що так само є вірним.

Задача 3. Вибрати по одному елементі з кожного стовпця й з кожного рядка, так щоб їхня сума була максимальною.

У цій задачі функція  й множина  залишаються колишніми, а сімейство незалежних підмножин  будуть утворювати такі множини, у яких всі елементи з різних стовпців і різних рядків і порожня множина.

Неважко бачити, що жадібний алгоритм вибере наступні елементи:

 і, які не є рішенням задачі, оскільки існує краще рішення -  і .

Виникає питання, у яких же випадках жадібний алгоритм дійсно вирішує поставлену задачу? На поставлене питання допоможе відповісти теорема, сформульована й доведена в [4, с.75-76].

Теорема 7.

 Для будь-якої функції  жадібний алгоритм знаходить незалежну множину  з найбільшою вагою, тоді й тільки тоді, коли  є матроїдом.

Дійсно, у нашім прикладі в задачах 1 і 2 - матроїд, а в задачі 3 таким не є, тому що не виконується аксіома М₃. Якщо розглянути  , тоді  одержали протиріччя з незалежністю хоча б одного із множин.

Висновок

 

У роботі були розглянуті такі питання, як:

Вивчення й визначення поняття відношення залежності.

Розглянуті деякі приклади відносин залежності.

Сформулювали й довели властивості теореми як для довільних, так і для транзитивних просторів залежності. Робота дала відповіді на всі питання, які були поставлені за мету.

Список літератури

1. Ван дер Варден Б.Л. Алгебра. – К., 2004

2. Кон П. Універсальна алгебра. – К., 2004.

3. Курош О. Г. Курс вищої алгебри. – К., 2003.

4. Новиков Ф. А. Дискретна математика для програмістів. – К., 2005

5. Фрид Е. Елементарне введення в абстрактну алгебру. – К., 2000