Линейное программирование

Негосударственное среднее профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

курсовая РАБОТА

по дисциплине Математические методы

Тема: Линейное программирование

Выполнил(а) студент(ка) курса, группы ПО-27 ЗС

Якушева Ольга Сергеевна

фамилия имя отчество

Руководитель работы Груздева Елена Юрьевна

ученая степень, звание, фамилия и инициалы

 

Содержание

Введение

Теоретическая часть

Математическое решение задачи

Заключение

Список использованной литературы

Приложение №1 (Excel)

Приложение №2 (Pascal)

 

Введение

Математическое программирование – область прикладной математики, объединяющая различные мат.методы и дисциплины.

Методы:

1.  Математическое программирование.

2.  Дифференциальные и разностные уравнения.

3.  Теория игр.

4.  Теория решений и т.д.

Классические задачи исследования операций:

·  Задачи диеты (задача о рационе).

·   Задача замены (динамическое программирование).

·  Задача коммивояжера (динамическое программирование).

·  Распределительные задачи.

·  Задача о назначениях.

·  Задача о размещении складов.

·  Задача о раскрое (линейное программирование).

·  Задача поиска.

·  Теория расписаний (метод дискретного программирования).

·  Управление запасами (линейное программирование).

·  Задачи массового обслуживания.

Методы математического программирования:

1.  Линейного программирование.

2.  Не линейное программирование.

3.  Динамическое программирование.

4.  Алгоритмы на графах.

5.  Система массового обслуживания (СМО).

6.  Методы прогнозирования.

7.  Имитационное прогнозирование.

8.  Теория игр.

9.  Теория принятия решений.

Теоретическая часть

Рассмотрим один из основных методов – линейное программирование.

Линейное программирование (далее ЛП) – задачи, в которых критерий оптимальности задается в виде линейной формы от входящих в него переменных, на эти переменные накладываются ограничения в виде линейных уравнений или линейных неравенств.

Основные задачи ЛП:

ü  Задача оптимизации межотраслевых потоков.

ü  Транспортные задачи.

ü  Подробнее поговорим про задачу об оптимальном выпуске продукции.

Требуется составить такой план выпуска продукции, который был бы технологически осуществлен по имеющимся ресурсам всех видов, удовлетворял бы задаваемым ограничениям на выпуске каждого вида продукции и в то же время приносил наибольшую прибыль предприятию.

Математическая модель любой задачи линейного программирования включает в себя:

·  максимум или минимум целевой функции (критерий оптимальности);

·  систему ограничений в форме линейных уравнений и неравенств;

·  требование неотрицательности переменных.

Для решения задач ЛП используют графический метод и симплекс-метод.

Математическое решение задачи

 

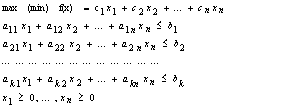
В общем виде задачу линейного программирования можно представить следующим образом:

Алгоритмы симплекса-метода позволяют также установить, является ли задача ЛП разрешимой.

Рассмотрим задачу линейного программирования симплекс методом. Предприятие располагает ресурсами сырья, рабочей силой и оборудованием, необходимым для производства любого из трех видов производимых товаров 1, 2, 3. Затраты ресурсов на изготовление единицы данного вида товаров; прибыль, получаемая от реализации единицы товара, а также запасы ресурсов указаны в таблице.

Вид ресурса	Затраты ресурса на единицу товара			Запас ресурса
	Товар 1	Товар 2	Товар 3
Сырье, кг.	4	8	4	120
Рабочая сила, ч.	6	2	3	160
Оборудование, станко-час.	2	2	4	400
Прибыль	10	8	6

 

Определить какой ассортимент товара надо выпускать, чтобы прибыль была максимальной.

Обозначим Товар 1 как х₁, Товар 2 – х₂, Товар 3 – х₃.

Z=10х1+8х2+6х3

Решим задачу симплекс методом.

Математическая модель должна быть в канонической форме, т.е. все ограничения в виде неравенств.

4x₁ + 8x₂ + 4x₃ ≤ 120

6x₁ + 2x₂ + 3x₃ ≤ 160

2x₁ + 2x₂ + 4x₃ ≤ 400

Введем новые переменные x₄, x₅, x₆.

4x₁ + 8x₂ + 4x₃ + x₄ ≤ 120

6x₁ + 2x₂ + 3x₃ + x₅ ≤ 160

2x₁ + 2x₂ + 4x₃ +x₆ ≤ 400

Находим исходные опорные решения и проверяем на оптимальность, для этого заполняем симплексную таблицу.

Ключевой элемент

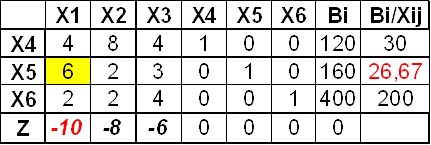
I опорное решение.

x₁=0, x₂=0, x₃=0, x₄=120, x₅=160, x₆=400, Z=0.

Если решение не оптимально, строим вторую симплекс-таблицу.

Находим ключевой элемент: выбираем столбец с наибольшей по модулю отрицательной оценкой, для этого столбца находим b_i/x_ij и выбираем минимальное значение, т.е. выбираем строку, на пересечении выбранного столбца и строки определяется ключевой элемент;

Ключевой элемент находится на пересечении столбца х₁ и строки х₅, т.е. меняем их местами. Свободные переменные x₅, x₂, x₃; базисные переменные x₁, x₄, x₆.

Во второй симплекс-таблице переписываем ключевую строку, разделив ее на ключевой элемент, заполняем базисные столбцы, остальные коэффициенты таблицы находим по правилу прямоугольника;

Получаем новое опорное решение и проверяем его на оптимальность,

Ключевой элемент

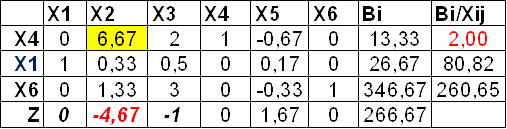
II опорное решение.

x₁=26,67, x₂=0, x₃=0, x₄=13,33, x₅=0, x₆=346,67, Z=266,67.

Данное решение не является оптимальным, т.к. в последней строке симплекс-таблицы находится отрицательное число – строим третью симплекс-таблицу.

Ключевой элемент находится на пересечении столбца х₂ и строки х₄, т.е. меняем их местами. Свободные переменные x₄, x₃, x₅; базисные переменные x₂, x₁, x₆.

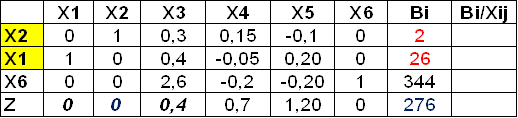
III опорное решение.

x1=26, x2=2, x3=0, x4=0, x5=0, x6=344, Z=276.

Третье опорное решение является оптимальным, так как последняя строка симплекс таблицы содержит только положительные элементы.

Подставляем в линейную функцию Z = 10*26 + 8*2 + 6*0 = 276.

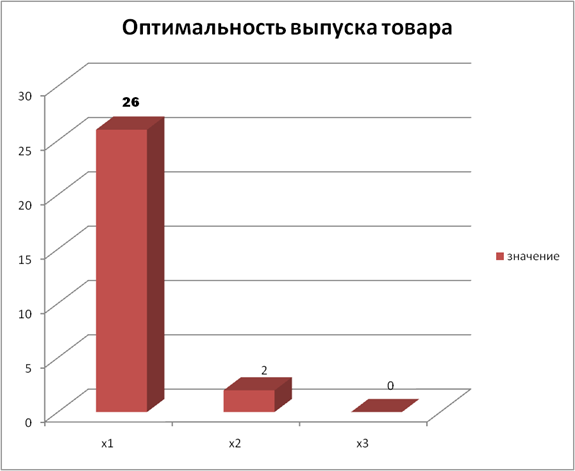
Оптимально производить Товар 1 – в количестве 26, Товар 2 – в количестве 2 и Товар 3 – в количестве 0.

Запрограммируем в MS Office Excel (Приложение№1) и в Pascal (Приложение№2). Данные и условия сформированы ранее.

Заключение

Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения. Тем не менее, сам факт полиномиальной сложности задач привёл к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 г. Метод внутренних точек, который, в отличие от симплекс-метода, обходит точки из внутренней части области допустимых значений, использует методы логарифмических барьерных функций нелинейного программирования, разработанные в 60-х гг. Фиако (Fiacco) и МакКормиком (McCormick). Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 г. советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешённой. Метод эллипсоидов имеет совершенно другую, некомбинаторную, природу, нежели симплекс-метод. Однако в вычислительном плане этот метод оказался неперспективным.

Список использованной литературы

 

-   А.И.Ларионов, Т.И.Юрченко “Экономико-математические методы в планировании: Учебник – М.: Высш.школа, 1984

-   Томас Х. Кормен и др. Глава 29. Линейное программирование // Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006.

-   В.И. Бодров, Т.Я. Лазарева, Ю.Ф. Мартемьянов «Математические методы принятия решений», Издательство ТГТУ, 2004

-   Вершик А. М. «O Л. В. Канторовиче и линейном программировании»

-   Большакова И. В., Кураленко М. В. «Линейное программирование. Учебно-методическое пособие к контрольной работе».

					Приложение №1
В правой части записываем запас ресурса.
Переменные
	x1	x2	x3
значение	26	2	0	ЦФ
коэф. ЦФ	10	8	6	276
Ограничения				лев.часть	знак	прав.часть
раб.сила, ч.	4	8	4	120	≤	120
сырье, кг.	6	2	3	160	≤	160
оборудование, станко-час.	2	2	4	56	≤	400

Приложение №2

PROGRAM SIMPLEX_METOD;

USES CRT;

LABEL ZN,ST,ELL,_END;

 TYPE MAS=ARRAY[1..30] OF REAL;

 MASB=ARRAY[1..30] OF STRING[3];

 MASX=ARRAY[1..30,1..30] OF REAL;

VAR Fo,FunctPr,B,H,Hnew,C,Cnew,CPr,CPrnew,FX:MAS;

 X,Xnew:MASX;

 BS,Bvsp,ZNAC:MASB;

 MIN,I1,I,J,Kx,Ky,Kit,NachKell,NachY,K_st:INTEGER;

 PriznacY,KLstr,KLst,ErrCode,Dop_X:INTEGER;

 P,P1,Mo,F0,Epsilon,Z:REAL;

 VSP,S,PrGomory:STRING;

 F:TEXT;

 DPx,DPy,Fm,Kell,Kstr:INTEGER;

 { Функция создания индексов }

FUNCTION SIMVB(V:INTEGER;S:CHAR):STRING;

 VAR M,Z:STRING;

BEGIN

 STR(V,M);

 Z:=S+M;

 SIMVB:=Z;

END;

 { Процедура записи данных в файл }

PROCEDURE SAVE(X1:REAL;K:STRING;Mstr:INTEGER);

VAR V:STRING;

BEGIN

ASSIGN(F,'SIMPLEX.DAT');

APPEND(F);

CASE Mstr OF

 0:WRITELN(F,'');

 1:BEGIN

 IF K=' ' THEN STR(X1:1:0,V) ELSE STR(X1:10:4,V);

 WRITE(F,V);

 WRITE(F,' ');

 END;

 2:WRITE(F,K);

 3:WRITELN(F,K);

END;

CLOSE(F);

END;

 { Определение дополнительных переменных }

PROCEDURE DOP_PER;

 BEGIN

 IF ZNAC[I1]='=' THEN

 BEGIN

 Kell:=Kell+1;Bvsp[Kell]:=SIMVB(DPy,'Y');

 DPy:=DPy+1;

 Xnew[I1,Kell]:=1;

 IF Fm=1 THEN FX[Kell]:=-1 ELSE FX[Kell]:=1;

 FunctPr[Kell]:=1;

 FOR I:=1 TO Kstr DO

 IF I<>I1 THEN Xnew[I,Kell]:=0;

 END;

 IF ZNAC[I1]='>=' THEN

 BEGIN

 Kell:=Kell+1;Bvsp[Kell]:=SIMVB(DPx,'X');

 DPx:=DPx+1;Dop_X:=Dop_X+1;

 Xnew[I1,Kell]:=-1;FX[Kell]:=0;

 FOR I:=1 TO Kstr DO

 IF I<>I1 THEN Xnew[I,Kell]:=0;

 Kell:=Kell+1;Bvsp[Kell]:=SIMVB(DPy,'Y');

 DPy:=DPy+1;

 Xnew[I1,Kell]:=1;

 IF Fm=1 THEN FX[Kell]:=-1 ELSE FX[Kell]:=1;

 FunctPr[Kell]:=1;

 FOR I:=1 TO Kstr DO

 IF I<>I1 THEN Xnew[I,Kell]:=0;

 END;

 IF ZNAC[I1]='<=' THEN

 BEGIN

 Kell:=Kell+1;Bvsp[Kell]:=SIMVB(DPx,'X');

 DPx:=DPx+1;Dop_X:=Dop_X+1;

 Xnew[I1,Kell]:=1;FX[Kell]:=0;

 FOR I:=1 TO Kstr DO

 IF I<>I1 THEN Xnew[I,Kell]:=0;

 END;

END;

{ Процедура сокращения Y }

PROCEDURE SOKR;

VAR P:INTEGER;

 BEGIN

 Kell:=Kell-1;

 FOR P:=NachKell+DOP_X TO Kell DO

 IF Bvsp[P]=BS[KLstr] THEN BEGIN

 FOR J:=P TO Kell DO

 Bvsp[J]:=Bvsp[J+1];

 FunctPr[J]:=FunctPr[J+1];

 Fx[J]:=Fx[J+1];

 FOR I:=1 TO Kstr DO

 Xnew[I,J]:=Xnew[I,J+1]

 END;

 END;

 { Процедура, выполняющая метод Гомори }

PROCEDURE GOMORY;

VAR MAX,Z:REAL;

BEGIN

 KLstr:=1;

 MAX:=H[1]-INT(H[1]);

 FOR I1:=2 TO Kstr DO

 IF (H[I1]-INT(H[I1]))>=MAX THEN BEGIN MAX:=H[I1]; KLstr:=I1;END;

 Kstr:=Kstr+1;

 Hnew[Kstr]:=H[KLstr]-INT(H[KLstr]);

 FOR I1:=1 TO Kell DO

 BEGIN

 Z:=INT(X[KLstr,I1]);

 IF X[KLstr,I1]<0 THEN Z:=Z-1;

 Xnew[Kstr,I1]:=X[KLstr,I1]-Z;

 END;

ZNAC[Kstr]:='>=';

END;

 { Процедура, выполняющая Симплекс метод }

PROCEDURE SIMPLEX;

 LABEL POVZNAC,NACH;

BEGIN

 { Подготовка к вводу данных }

NachKell:=Kell;

DPx:=Kell+1;DPy:=1;

Kx:=1;Ky:=4;

Epsilon:=0.00001;

CLRSCR;

WRITELN('Введите систему уравнений:');

WRITELN('(коэффициенты при всех Х,знак и свободные члены)');

 { Ввод данных }

 FOR I:=1 TO Kstr DO

 BEGIN

POVZNAC:

 WRITELN('Введите ',I,'-е уравнение:');

 { Ввод коэффициентов при X в I-том уравнении }

 FOR J:=1 TO Kell DO

 BEGIN

 GOTOXY(Kx,Ky);Kx:=Kx+6;

 READLN(Xnew[I,J]);

 END;

 { Ввод знака в I-том уравнении }

 Kx:=Kx+6;GOTOXY(Kx,Ky);READLN(ZNAC[i]);

 {Проверка введенного знака на правильность}

 IF (ZNAC[i]<>'>=') AND (ZNAC[i]<>'=') AND (ZNAC[i]<>'<=')

 THEN BEGIN

 WRITELN('Неправильно задан знак');

 Ky:=Ky+3;Kx:=1;

 GOTO POVZNAC;

 END;

 IF (ZNAC[i]='=') OR (ZNAC[i]='>=') THEN PriznacY:=1;

 { Ввод свободного члена в I-том уравнении }

 Kx:=Kx+6;GOTOXY(Kx,Ky);READ(B[i]);

 Kx:=1;

 Ky:=Ky+2;

 END;

WRITELN('Введите коэффициенты при Х в целевой функции:');

 { Ввод коэффициентов при Х в целевой функции }

 FOR J:=1 TO Kell DO

 BEGIN

 GOTOXY(Kx,Ky);Kx:=Kx+6;

 READ(FX[J]);

End;

{ Подготовка индексации X }

FOR J:=1 TO Kell DO

 Bvsp[J]:=SIMVB(J,'X');

 { Определение дополнительных переменных }

FOR I1:=1 TO Kstr DO

 DOP_PER;

 { Замена оптимальной функции с MAX на MIN при наличии

 в базисе Y-ков если идет исследование на минимум }

MIN:=0;

IF (Fm=1) AND (PriznacY=1) THEN

 BEGIN

 MIN:=Fm;Fm:=2;

 FOR J:=1 TO Kell DO

 FX[J]:=-FX[J];

 END;

 { Сортировка дополнительных переменных по индексу }

FOR I1:=NachKell+1 TO Kell DO

 FOR J:=I1+1 TO Kell DO

 IF Bvsp[J]<Bvsp[I1] THEN

 BEGIN

 VSP:=Bvsp[J];Bvsp[J]:=Bvsp[I1];Bvsp[I1]:=VSP;

 P:=FX[J];FX[J]:=FX[I1];FX[I1]:=P;

 P:=FunctPr[J];FunctPr[J]:=FunctPr[I1];FunctPr[I1]:=P;

 FOR I:=1 TO Kstr DO

 BEGIN

 P:=Xnew[I,I1];Xnew[I,I1]:=Xnew[I,J];Xnew[I,J]:=P;

 END;

 END;

Kit:=1;

CLRSCR;

 { Подготовка столбцов C,B,H }

 FOR I:=1 TO Kstr DO

 BEGIN

 Hnew[i]:=B[i];

 FOR J:=NachKell+1 TO Kell DO

 IF Xnew[I,J]=1 THEN

 BEGIN

 BS[i]:=Bvsp[J];

 Cnew[i]:=FX[J];

 CPrnew[i]:=FunctPr[J];

 END;

 END;

NACH:;

REPEAT

PriznacY:=0;

 { Передача данных в исходные переменные c обнулением

чисел, модулю меньших чем 0.00001 }

FOR I:=1 TO Kstr DO

 BEGIN

 IF INT(10000*Hnew[i])=0 THEN H[i]:=+0 ELSE H[i]:=Hnew[i];

 C[i]:=Cnew[i];

 CPr[i]:=CPrnew[i];

 IF BS[i][1]='Y' THEN PriznacY:=1;

 FOR J:=1 TO Kell DO

 IF INT(10000*Xnew[I,J])=0 THEN X[I,J]:=+0 ELSE X[I,J]:=Xnew[I,J];

 END;

{ Обнуление и вывод индексации элементов индексной строки }

SAVE(0,' C Б H ',2);

FOR J:=1 TO Kell DO

 BEGIN

 SAVE(0,Bvsp[J],2);

 P1:=LENGTH(Bvsp[J]);

 IF P1=2 THEN SAVE(0,' ',2);

 SAVE(0,' ',2);

 Fo[J]:=0;

 END;

SAVE(0,'',0);

{ Вывод Симплекс-таблицы }

P1:=0;

FOR I:=1 TO Kstr DO

 BEGIN

 IF CPr[i]=1 THEN

 IF C[i]<0 THEN SAVE(0,'-M ',2)

 ELSE SAVE(0,'+M ',2)

 ELSE SAVE(C[i],'',1);

 SAVE(0,BS[i],2);

 P1:=LENGTH(BS[i]); IF P1=2 THEN SAVE(0,' ',2);

 SAVE(0,' ',2);SAVE(H[i],'',1);

 FOR J:=1 TO Kell DO

 SAVE(X[I,J],'',1);

 SAVE(0,'',0);

 END;

 { Вычисление значений в индексной строке }

F0:=0;

FOR J:=1 TO Kell DO

 Fo[J]:=0;

FOR I1:=1 TO Kstr DO

 BEGIN

 IF PriznacY=1 THEN

 IF BS[I1][1]='Y' THEN

 BEGIN

 F0:=F0+H[I1];

 FOR J:=1 TO Kell DO

 Fo[J]:=Fo[J]+X[I1,J];

 END;

 IF PriznacY=0 THEN

 BEGIN

 F0:=F0+H[I1]*C[I1];

 FOR J:=1 TO Kell DO

 Fo[J]:=Fo[J]+C[I1]*X[I1,J];

 END;

FOR J:=1 TO Kell DO

 IF Bvsp[J][1]='Y' THEN Fo[J]:=+0

 ELSE IF ABS(Fo[J])<Epsilon THEN Fo[J]:=+0;

 END;

 { Вывод значений целевой функции }

SAVE(0,' ',2);SAVE(F0,'',1);

FOR J:=1 TO Kell DO

 BEGIN

 IF PriznacY<>1 THEN Fo[J]:=Fo[J]-FX[J];

 SAVE(Fo[J],'',1);

 END;

SAVE(0,'',0);

{ Проверка условия оптимальности }

P:=0;

FOR J:=1 TO Kell DO

 IF Fm=1 THEN IF Fo[J]<-Epsilon THEN

 BEGIN

 P:=1;

 CONTINUE;

 END ELSE

 ELSE IF Fo[J]>Epsilon THEN

 BEGIN

 P:=1;

 CONTINUE;

 END;

IF P<>1 THEN

 BEGIN

 SAVE(0,'В ',2);SAVE(Kit,' ',1);

 SAVE(0,'-й итерации было получено оптимальное решение',3);

 SAVE(0,'т.к. при исследовании на ',2);

 IF Fm=1 THEN

 SAVE(0,'МАКСИМУМ индексная строка не содержит отицательных элементов.',3)

 ELSE

 SAVE(0,'МИНИМУМ индексная строка не содержит положительных элементов.',3);

 FOR I1:=1 TO Kstr DO

 IF BS[I1][1]='Y' THEN

 BEGIN

 SAVE(0,'Но т.к. из базиса не выведены все Y, то ',3);

 SAVE(0,'можно сделать вывод, что РЕШЕНИЙ НЕТ',3);

 HALT;

 END;

{округление значений массива Х до целого числа, если разность округленного и обычного значений по модулю меньше чем 0.00001}

FOR I:=1 TO Kstr DO

 BEGIN

 Z:=ROUND(H[i]);

 IF ABS(Z-H[i])<Epsilon THEN H[i]:=ROUND(H[i]);

 FOR J:=1 TO Kell DO

 BEGIN

 IF X[I,J]<0 THEN Z:=ROUND(X[I,J]);

 IF ABS(Z-X[I,J])<Epsilon THEN X[I,J]:=ROUND(X[I,J]);

 END;

 END;

 { Проверка целочисленности решения }

P1:=0;

FOR I:=1 TO Kstr DO

 BEGIN

 IF INT(10000*FRAC(H[i]))<>0 THEN BEGIN P1:=1;CONTINUE; END;

 FOR J:=1 TO Kell DO

 IF BS[i]=Bvsp[J] THEN

 FOR I1:=1 TO Kstr DO

 IF ABS(FRAC(X[I1,J]))>=Epsilon THEN BEGIN P1:=1;CONTINUE; END;

 END;

 { Составление новой базисной строки для целочисленного решения }

 IF (PrGomory='Y') AND (P1=1) THEN

 BEGIN

 GOMORY;

 NachKell:=Kell;

 I1:=Kstr;DPy:=1;

 DOP_PER;

 BS[Kstr]:=Bvsp[Kell];

 CPrnew[Kstr]:=FunctPr[Kell];

 Cnew[Kstr]:=FX[Kell];

 GOTO NACH;

 END;

 IF P1=0 THEN SAVE(0,'Данное решение является целочисленым.',3);

 SAVE(0,'При этом:',3);

 IF MIN=1 THEN BEGIN F0:=-F0;Fm:=MIN; END;

 IF Fm=1 THEN

 SAVE(0,'Fmax=',2)

 ELSE

 SAVE(0,'Fmin=',2);

 SAVE(F0,'',1);

 SAVE(0,'',0);

 FOR I1:=1 TO Kstr DO

 BEGIN

 SAVE(0,' ',2);

 SAVE(0,BS[I1],2);SAVE(0,'=',2);

 SAVE(H[I1],'',1);

 SAVE(0,'',0);

 END;

 HALT;

END;

{ Нахождение ключевого столбца }

KLst:=1;Mo:=0;

FOR J:=1 TO Kell DO

 IF Fm=1 THEN

 IF Fo[J]<Mo THEN Mo:=Fo[J];

FOR J:=1 TO Kell DO

 BEGIN

 IF Bvsp[J][1]<>'Y' THEN

 IF Fm=1 THEN

 BEGIN

 IF Fo[J]<0 THEN

 IF Fo[J]>=Mo THEN

 BEGIN

 Mo:=Fo[J]; KLst:=J;

 END;

 END

 ELSE

 BEGIN

 IF Fo[J]>0 THEN

 IF Fo[J]>=Mo THEN

 BEGIN

 Mo:=Fo[J]; KLst:=J;

 END;

 END;

 END;

 SAVE(0,'Ключевой столбец: ',2);SAVE(KLst,' ',1);

 { Нахождение ключевой строки }

P1:=0;K_st:=0;

FOR J:=1 TO Kell DO

 IF ABS(Mo-Fo[J])<Epsilon THEN

 BEGIN

 K_st:=K_st+1;

 FOR I:=1 TO Kstr DO

 IF X[I,KLst]>0 THEN BEGIN B[i]:=H[i]/X[I,KLst]; P:=B[i];KLstr:=I; END

 ELSE BEGIN B[i]:=-1; P1:=P1+1; END;

 END;

IF P1=Kstr*K_st THEN

 BEGIN

 SAVE(0,'',0);

 SAVE(0,'РЕШЕНИЙ НЕТ т.к. невозможно определить ключевую строку',3);

 HALT;

 END;

P1:=0;

FOR J:=1 TO Kell DO

 IF ABS(Mo-Fo[J])<Epsilon THEN

 FOR I:=1 TO Kstr DO

 IF B[i]>=0 THEN BEGIN

 IF B[i]<P THEN IF Bvsp[KLst]<>BS[i] THEN BEGIN P:=B[i]; KLstr:=I; END;

 IF INT(10000*B[i])=INT(10000*P) THEN

 IF (BS[i][1]='Y') AND (BS[KLstr][1]='X') THEN

 IF Bvsp[KLst]<>BS[i] THEN BEGIN P:=B[i]; KLstr:=I; END;

 END;

SAVE(0,'Ключевая строка: ',2);SAVE(KLstr,' ',1);

SAVE(0,'',0);

FOR I:=1 TO Kstr DO

 IF Bvsp[KLst]=BS[i] THEN

 BEGIN

 SAVE(0,'РЕШЕНИЙ НЕТ т.к. в базисном столбце уже есть ',3);

 SAVE(0,'такая переменная.',3);

 HALT;

 END;

 { Вызов процедуры сокращения Y }

If CPr[KLstr]=1 then SOKR;

{ Построение следующей Симплекс-таблицы }

BS[KLstr]:=Bvsp[KLst];

Cnew[KLstr]:=FX[KLst];

CPrnew[KLstr]:=FunctPr[KLst];

FOR I:=1 TO Kstr DO

 BEGIN

 IF I=KLstr THEN Hnew[i]:=H[i]/X[KLstr,KLst]

 ELSE Hnew[i]:=H[i]-(H[KLstr]*X[I,KLst]/X[KLstr,KLst]);

 FOR J:=1 TO Kell DO

 BEGIN

 IF (I=KLstr) AND (J=KLst) THEN Xnew[I,J]:=1;

 IF (I=KLstr) AND (J<>KLst) THEN Xnew[I,J]:=X[I,J]/X[KLstr,KLst];

 IF (I<>KLstr) AND (J=KLst) THEN Xnew[I,J]:=0;

 IF (I<>KLstr) AND (J<>KLst) THEN

 Xnew[I,J]:=X[I,J]-(X[KLstr,J]*X[I,KLst]/X[KLstr,KLst]);

 END;

 END;

KLst:=0;KLstr:=0;

Kit:=Kit+1;

UNTIL (Kit=0);

END;

 { Основная программа }

BEGIN

CLRSCR;

Kit:=0;Dop_X:=0;

ASSIGN(F,'SIMPLEX.DAT');

REWRITE(F);

CLOSE(F);

ST:;

 WRITE('Введите кол-во строк:');READLN(Kstr);

 IF Kstr>10 THEN

 BEGIN

 WRITELN('Программа не расчитана на введенное кол-во строк!');

 GOTO ST;

 END;

ELL:

 WRITE('Введите кол-во элементов:');READLN(Kell);

 IF Kell>10 THEN

 BEGIN

 WRITELN('Программа не расчитана на введенное кол-во элементов!');

 GOTO ELL;

 END;

ZN:

 WRITE('Исследуем на МАКСИМУМ(1) или МИНИМУМ(2):');READLN(Fm);

 IF (Fm<>1) AND (Fm<>2) THEN

 BEGIN

 WRITELN('Введите снова');GOTO ZN;

 END;

 WRITE('Целочисленное решение(Y/N): ');READLN(PrGomory);

 IF (PrGomory='Y') OR (PrGomory='y') THEN PrGomory:='Y' ELSE PrGomory:='N';

 { Вызов процедуры SIMPLEX}

SIMPLEX;

END.

Исходные данные

 Z = 10х₁+8х₂+6х₃

C: B: N: (Bi) X1 X2 X3 Y1 Y2 Y3

 

+M Y1 120.0000 4.0000 8.0000 4.0000 1.0000 0.0000 0.0000

+M Y2 160.0000 6.0000 2.0000 3.0000 0.0000 1.0000 0.0000

+M Y3 400.0000 2.0000 2.0000 4.0000 0.0000 0.0000 1.0000

680.0000 12.0000 12.0000 11.0000 0.0000 0.0000 0.0000

Klu4evoy stolbec: 2 Klu4evaya stroka: 1

 C: B: N: X1 X2 X3 Y2 Y3

 -8.0000 X2 15.0000 0.5000 1.0000 0.5000 0.1250 0.0000

+M Y2 130.0000 5.0000 0.0000 2.0000 -0.2500 1.0000

+M Y3 370.0000 1.0000 0.0000 3.0000 -0.2500 0.0000

 500.0000 6.0000 0.0000 5.0000 0.0000 0.0000

Klu4evoy stolbec: 1 Klu4evaya stroka: 2

 C: B: N: X1 X2 X3 Y3

 -8.0000 X2 2.0000 0.0000 1.0000 0.3000 0.1500

-10.0000 X1 26.0000 1.0000 0.0000 0.4000 -0.0500

+M Y3 344.0000 0.0000 0.0000 2.6000 -0.2000

 344.0000 0.0000 0.0000 2.6000 0.0000

В 3 -y iteracii bilo polu4eno optimalnoe reshenie

no t.k. iz bazisa nevivedeni vse Y, to

mojno sdelat vivod, chto resheniy NET

X1 = 26

X2 = 2

X3 = 0

Z = 10 * 26 + 8 * 2 + 6 * 0 = 276