Навигация
Шаг. Геометрическая иллюстрация статистических наблюдений
4 шаг. Геометрическая иллюстрация статистических наблюдений
1-ый показатель
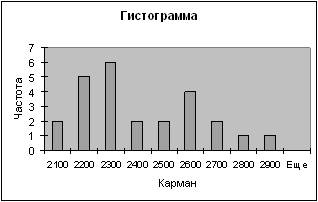
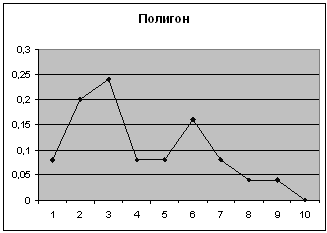
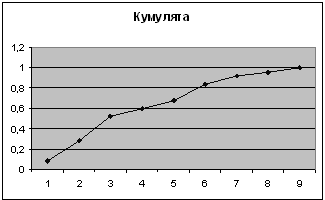
| Карман | Частота | P=m/n | Кумулята |
| 2100 | 2 | 0,08 | 0,08 |
| 2200 | 5 | 0,2 | 0,28 |
| 2300 | 6 | 0,24 | 0,52 |
| 2400 | 2 | 0,08 | 0,6 |
| 2500 | 2 | 0,08 | 0,68 |
| 2600 | 4 | 0,16 | 0,84 |
| 2700 | 2 | 0,08 | 0,92 |
| 2800 | 1 | 0,04 | 0,96 |
| 2900 | 1 | 0,04 | 1 |
| Еще | 0 | 0 |
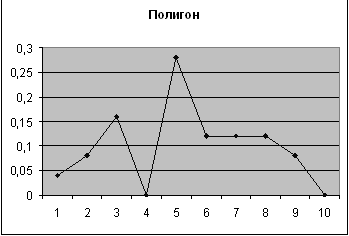
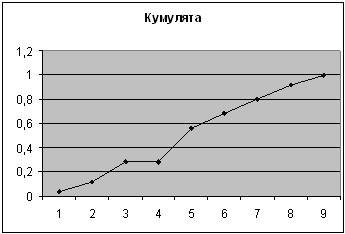
2-ой показатель
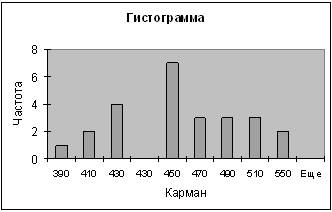
| Карман | Частота | P=m/n | Кумулята |
| 390 | 1 | 0,04 | 0,04 |
| 410 | 2 | 0,08 | 0,12 |
| 430 | 4 | 0,16 | 0,28 |
| 430 | 0 | 0 | 0,28 |
| 450 | 7 | 0,28 | 0,56 |
| 470 | 3 | 0,12 | 0,68 |
| 490 | 3 | 0,12 | 0,8 |
| 510 | 3 | 0,12 | 0,92 |
| 550 | 2 | 0,08 | 1 |
| Еще | 0 | 0 |
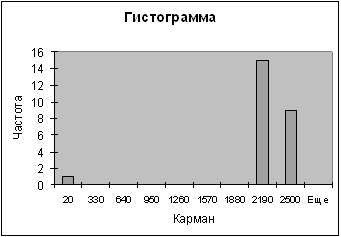
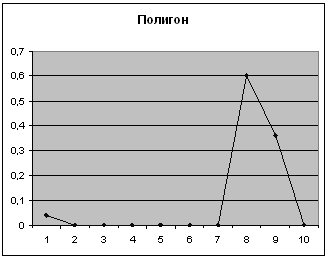
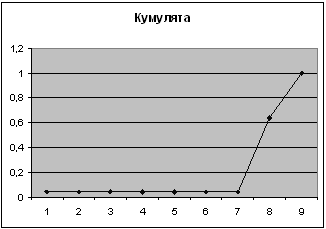
3-ий показатель
| Карман | Частота | P=m/n | Кумулята |
| 20 | 1 | 0,04 | 0,04 |
| 330 | 0 | 0 | 0,04 |
| 640 | 0 | 0 | 0,04 |
| 950 | 0 | 0 | 0,04 |
| 1260 | 0 | 0 | 0,04 |
| 1570 | 0 | 0 | 0,04 |
| 1880 | 0 | 0 | 0,04 |
| 2190 | 15 | 0,6 | 0,64 |
| 2500 | 9 | 0,36 | 1 |
| Еще | 0 | 0 |
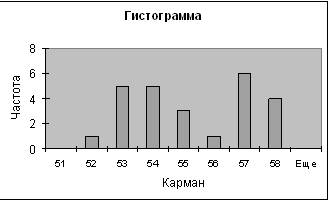
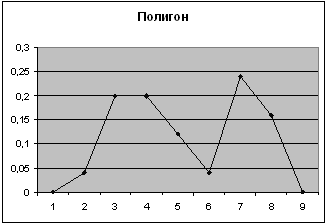
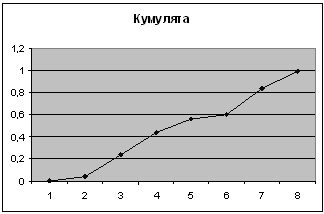
4-ый показатель
| Карман | Частота | P=m/n | Кумулята |
| 51 | 0 | 0 | 0 |
| 52 | 1 | 0,04 | 0,04 |
| 53 | 5 | 0,2 | 0,24 |
| 54 | 5 | 0,2 | 0,44 |
| 55 | 3 | 0,12 | 0,56 |
| 56 | 1 | 0,04 | 0,6 |
| 57 | 6 | 0,24 | 0,84 |
| 58 | 4 | 0,16 | 1 |
| Еще | 0 | 0 |
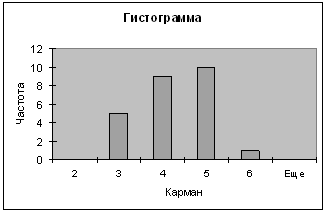
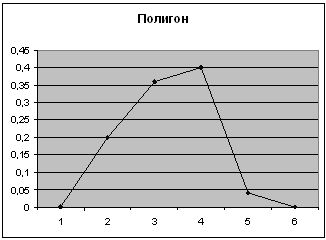
5-ый показатель
| Карман | Частота | P=m/n | Кумулята |
| 2 | 0 | 0 | 0 |
| 3 | 5 | 0,2 | 0,2 |
| 4 | 9 | 0,36 | 0,56 |
| 5 | 10 | 0,4 | 0,96 |
| 6 | 1 | 0,04 | 1 |
| Еще | 0 | 0 |

Этап №2. Однофакторная регрессия
1 шаг. Сравнение 1-го со 2-м:
Моделирование экономических процессов с помощью математических зависимостей заключается в подборе вида функции, которая гипотетически описывает эти процессы.
В нашем случае в качестве такой функции выбираем линейную зависимость между факторами.
Для этого введем следующие показатели:
Y – розничный товарооборот государственной и кооперативной торговли на душу населения
Х – среднемесячная денежная заработная плата рабочих и служащих
Тогда зависимость между ними будет характеризоваться следующим уравнением:
![]()
На основе данных, указанных в таблице 1, рассчитаем параметры модели, оценив ее статистическую надежность и адекватность реальным условиям.
2 шаг. Оценка параметров модели с помощью метода наименьших квадратов
Параметры модели нужно оценить по методу наименьших квадратов, т.к. он обеспечивает минимальную дисперсию опытных данных и в случае линейных зависимостей является наилучшим.
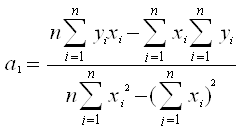
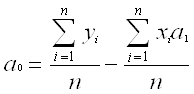
Похожие работы
... функциональную связь между переменными, либо они недостаточно варьируются, чтобы можно было отличить влияние одного фактора от влияния другого. Последняя проблема получила в эконометрическом моделировании название «мультиколлинеарности». В отличие от экспериментальных наук, у отдельного исследователя, изучающего экономические процессы, как правило, нет возможности сколько-нибудь заметно на них ...
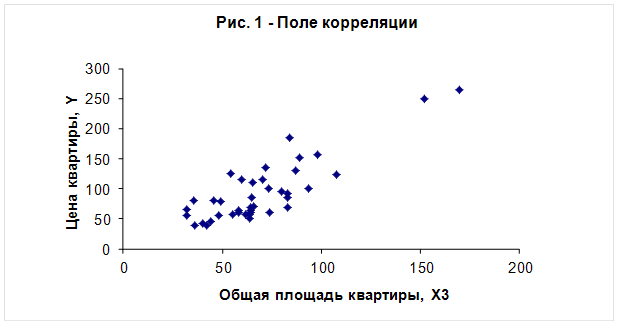
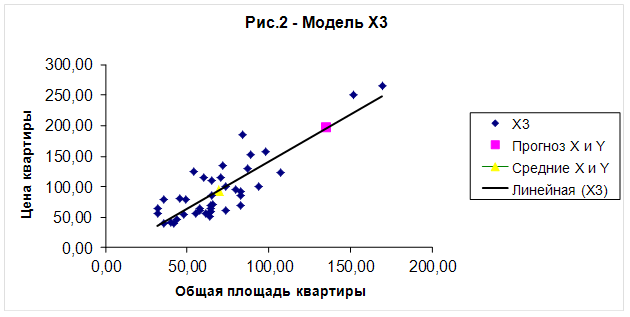
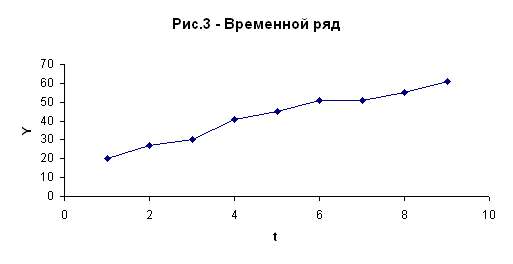
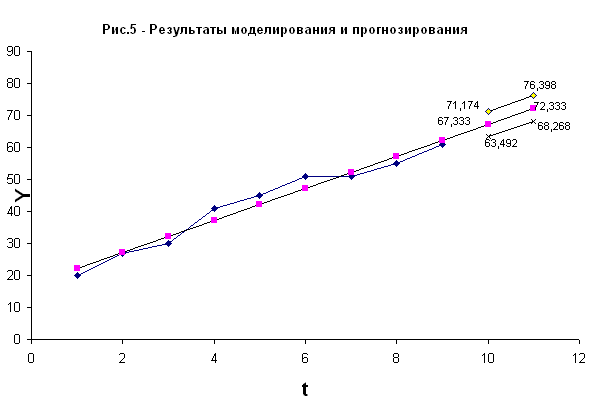
... или 16,4%, тогда как доля влияния фактора общая площадь – 0,836 или 83,6%. Задача №2. Исследование динамики экономического показателя на основе анализа одномерного временного ряда Таблица 6– Исходные данные t 1 2 3 4 5 6 7 8 9 yt 20 27 30 41 45 51 51 55 61 1. Выявление аномальных наблюдений Построим график временного ряда Для выявления аномальных наблюдений ...
... 807417 6 8,34207 210,6129 Выводы: 1. Решена задача парной регрессии методом наименьших квадратов. 2. Низкая достоверность результатов объясняется рядом причин: - собрано малое количество статистических данных, выбраны случайные районы за небольшой отрезок времени; - в учебных целях добавлены случайные точки, зависящие от порядкового номера студента и числа студентов в группе; - расходы ...
... Федерации в 1996 году издано Методические рекомендации по планированию, учету и калькулированию себестоимости продукции (работ, услуг) в сельском хозяйстве. [13, с.124] Методические рекомендации призваны обеспечить единство состава и классификации затрат, методов их учета, исчисления себестоимости продукции во всех сельскохозяйственных организациях. Но указанные Методические рекомендации, по ...

0 комментариев