Навигация
Линейный дискриминантный анализ
1.2 Линейный дискриминантный анализ
Выдвигаются предположения:
1) имеются разные классы объектов;
2) каждый класс имеет нормальную функцию плотности от k переменных
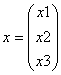 ;
;
![]() , (1.1)
, (1.1)
rде µ (i) - вектор математических ожиданий переменных размерности k;
![]() - ковариационная матрица при n=n;
- ковариационная матрица при n=n;
![]() - обратная матрица.
- обратная матрица.
Матрица ![]() - положительно определена.
- положительно определена.
В случае если параметры известны дискриминацию можно провести следующим образом.
Имеются функции плотности ![]() нормально pacпределенных классов. Задана точка х в пространстве k измерений. Предполагая, что имеет наибольшую плотность, необходимо отнести точку х к i-му классу. Существует доказательство, что если априорные вероятности для определяемых точек каждого класса одинаковы и потери при неправильной классификации i-й группы в качестве j-й не зависят от i и j, то решающая процедура минимизирует ожидаемые потери при неправильной классификации.
нормально pacпределенных классов. Задана точка х в пространстве k измерений. Предполагая, что имеет наибольшую плотность, необходимо отнести точку х к i-му классу. Существует доказательство, что если априорные вероятности для определяемых точек каждого класса одинаковы и потери при неправильной классификации i-й группы в качестве j-й не зависят от i и j, то решающая процедура минимизирует ожидаемые потери при неправильной классификации.
Ниже приведен пример оценки параметра многомерногo нормального pacпределения µ и Σ.
µ и Σ мoгyт быть оценены по выборочным данным: ![]() и
и ![]() для классов. Задано l выборок
для классов. Задано l выборок ![]() из некоторых классов. Математические ожидания
из некоторых классов. Математические ожидания ![]() мoгyт быть оценены средними значениями
мoгyт быть оценены средними значениями
![]() (1.2)
(1.2)
Несмещенные оценки элементов ковариационной матрицы Σ есть
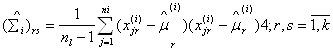 (1.3)
(1.3)
Cледовательно, можно определить![]() и
и ![]() по l выборкам в каждом классе при помощи (1.2), (1.3), получив оценки, точку х необходимо отнести к классу, для которой функция f(х) максимальна.
по l выборкам в каждом классе при помощи (1.2), (1.3), получив оценки, точку х необходимо отнести к классу, для которой функция f(х) максимальна.
Необходимо ввести предположение, что все классы, среди которых должна проводиться дискриминация, имеют нормальное распределение с одной и той же ковариационной матрицей Σ.
В результате существенно упрощается выражение для дискриминантной функции.
Класс, к которому должна принадлежать точка х, можно определить на
основе неравенства
![]()
![]() (1.4)
(1.4)
Необходимо воспользоваться формулой (1.1) для случая, когда их ковариационные матрицы равны:![]() , а
, а ![]() ( есть вектор математических ожиданий класса i. Тогда (1.4) можно представить неравенством их квадратичных форм
( есть вектор математических ожиданий класса i. Тогда (1.4) можно представить неравенством их квадратичных форм
![]() (1.5)
(1.5)
Если имеется два вектора Z и W, то скалярное произведение можно записать ![]() . В выражении (1.5) необходимо исключить
. В выражении (1.5) необходимо исключить ![]() справа и слева, поменять у всех членов суммы знаки. Теперь преобразовать
справа и слева, поменять у всех членов суммы знаки. Теперь преобразовать
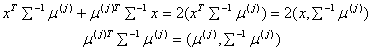
Аналогично проводятся преобразования по индексу i. Необходимо сократить правую и левую часть неравенства (1.5) на 2 и, используя запись квадратичных форм, получается
![]() (1.6)
(1.6)
Необходимо ввести обозначения в выражение (1.6):
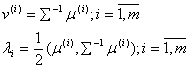
Тогда выражение (1.6) примет вид
![]() (1.7)
(1.7)
Следствие: проверяемая точка х относится к классу i, для которого линейная функция
![]() (1.8)
(1.8)
Преимущество метода линейной дискриминации Фишера заключается в линейности дискриминантной функции (1.8) и надежности оценок ковариационных матриц классов.
Пример
Имеются два класса с параметрами![]() и
и ![]() . По выборкам из этих совокупностей объемом n1 n2 получены оценки
. По выборкам из этих совокупностей объемом n1 n2 получены оценки ![]() и
и ![]() . Первоначально проверяется гипотеза о том, что ковариационные матрицы
. Первоначально проверяется гипотеза о том, что ковариационные матрицы ![]()
![]() равны. В случае если оценки
равны. В случае если оценки ![]() и
и ![]() статистически неразличимы, то принимается, что
статистически неразличимы, то принимается, что ![]() и строится общая оценка
и строится общая оценка ![]() , основанная на суммарной выборке объемом n1+n2 , после чего строится линейная дискриминантная функция Фишера (1.8).
, основанная на суммарной выборке объемом n1+n2 , после чего строится линейная дискриминантная функция Фишера (1.8).
Похожие работы
... период подготовки планов. Еще одна категория систем, используемых для бюджетирования - корпоративные системы управления (ERP-системы). ERP (Enterprise Resource Planning) - автоматизация и оптимизация внутренних бизнес-процессов, планирование как материальных, так и финансовых ресурсов в масштабе предприятия; - используется для описания компонентов "производство", "логистика", "финансы". ERP- ...
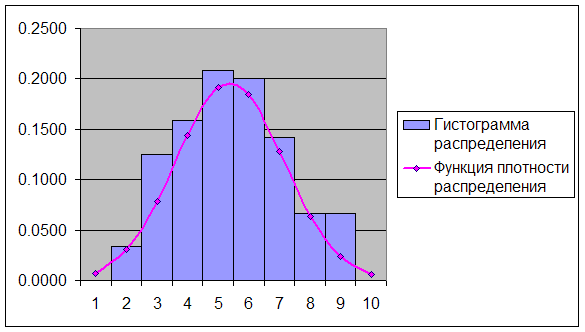
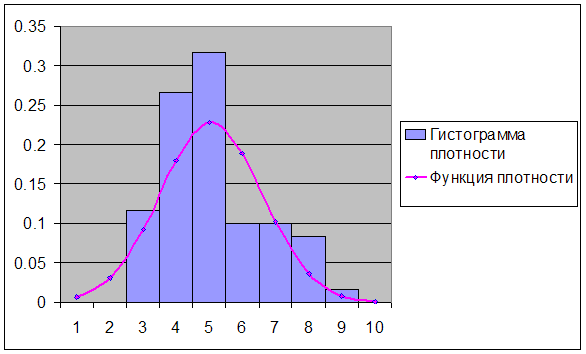
... критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 8-3=5 находим Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины . Для случайной величины : Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле , где - объем выборки, - шаг (разность между ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... взаимосвязи и взаимодействие подразделений с аналогичными функциями на разных уровнях единой организационной и управленческой структуры. Такая структура создает упорядоченность и организованность системы таможенных органов при выполнении возложенных на них функций. Рассмотрим современную организационную структуру таможенных органов. ГТК России имеет дифференцированную и разветвленную структуру. ...
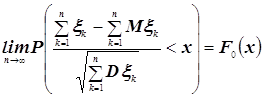
0 комментариев