Навигация
Имея корни полиномов – делителей g(x) можно найти их функции минимума, и следовательно найти g(x)
21743
знака
0
таблиц
12
изображений
3. Имея корни полиномов – делителей g(x) можно найти их функции минимума, и следовательно найти g(x) .
4. 
содержит корни g(x).
Таким образом, нахождение порождающего полинома по степеням его корней сводится к нахождению минимальных полиномов для элементов поля с соответствующей степенью.
,
где 
минимальный полином.
2.1 Нахождение порождающего полинома по последовательности степеней корней
В таблице из приложения Г книги [1] содержатся параметры циклических кодов и последовательности степеней корней. Мы рассматриваем только коды тривиальной длины. Часть этой таблицы указана в приложении А данной работы. В таблице из приложения В книги [1] указаны неприводимые полиномы над GF(2). Укороченное представление такой таблицы также есть в приложении Б данной работы.
Алгоритм нахождения порождающего полинома:
1. Исходя из длины выбранного кода, построить расширение 
поля 
по модулю неприводимого полинома над 
степень которого равна m. Где m находится из следующего соотношения: 
.
2. Для каждого корня построить циклотомический класс.
3. Для каждого корня найти минимальный полином.
4. Перемножить полученные минимальные полиномы по правилам для .
Рассмотрим каждый шаг более подробно на примере кода (15,5,7) . Для такого кода в таблице циклических кодов указаны следующие степени корней {1,3,5}.
Шаг 1. Построение .
Длина n заданного кода равна 15. Так как 
, m = 4. Будем строить 
. Так как m = 4, то из таблицы неприводимых полиномов выберем полином четвертой степени 
, по модулю которого будет построено . Как построить расширение поля, было рассмотрено в 1.4.3.
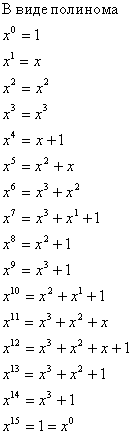
Таблица 3. .
Шаг 2. Построение циклотомических классов.
Последовательность степеней корней для данного кода - {1,3,5}. Для каждого элемента последовательности построим циклотомический класс, при помощи формулы 
. Подробно построение циклотомических классов описано в 1.4.4
Для корня со степенью 1 это {1,2,4,8}.
Для корня со степенью 3 это {3,6,9,12}.
Для корня со степенью 5 это {5,10}.
Шаг 3. Нахождение минимальных полиномов.
Исходя из теоремы 2, для каждого корня найдем его минимальный полином, подробно нахождение минимальных полиномов описано выше.
Для корня со степенью 1:
Для корня со степенью 3: m3(x) = (x – a3 ) (x – a6 ) (x – a9 ) (x – a12 ) = x4 + x3+ x2 + x1+1.
Для корня со степенью 5: m5(x) = (x – a5 ) (x – a10 ) = x2 + x+1
Шаг 4. Нахождение порождающего полинома.
Из 1.5 , где это минимальные полиномы для заданных корней, то было получено, что
Заключение
В данной работе рассмотрено краткое математической описание циклических кодов с точки зрения алгебры конечных полей, которого вполне достаточно для решения задачи нахождения порождающего полинома кода, используя его корни. Безусловно, материал изложен в очень сжатой форме и многое нужно принять, как аксиому. Изначально данная работа задумывалась, как описание алгоритма нахождения полинома с некоторыми комментариями к каждому шагу, но в процессе описания алгоритма, оказалось, что без краткой теории конечных полей это сделать невозможно.
Список литературы
1. У. Питерсон, Э. Уэлдон. «Коды, исправляющие ошибки»: Москва: Мир, 1976.
2. Р. Блейхут. «Теория и практика кодов исправляющих ошибки»: Москва: Мир, 1986. - 576с.
3. Жуков А.Б. , Каменский С.В. Передача сообщений. – НГТУ, 2003.
Приложения
Приложение А. Таблица неприводимых полиномов над GF(2).
Приложение Б. Таблица двоичных некоторых циклических кодов тривиальной длины
Похожие работы
... , если его длина n=qm-1 над GF(q). Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным. Общее свойство кодовых слов циклического кода - это их делимость без остатка на некоторый многочлен g(x), называемый порождающим. Результатом деления двучлена xn+1 на многочлен g(x) является проверочный многочлен h(x). При декодировании циклических кодов используются ...
... кодов используются так называемые сверточные коды, контрольные биты, в которых формируются непрерывно из информационных и контрольных бит смежных блоков. Выводы Таким образом, в результате написания реферата, пришли к выводу, что коды Боуза-Чоудхури-Хоквингхема – это широкий класс циклических кодов, способных исправлять многократные ошибки. БЧХ-коды играют заметную роль в теории и практике ...
... ? 8. Какими программами можно воспользоваться для устранения проблем и ошибок, обнаруженных программой Sandra? Раздел 3. Автономная и комплексная проверка функционирования и диагностика СВТ, АПС и АПК Некоторые из достаточно интеллектуальных средств вычислительной техники, такие как принтеры, плоттеры, могут иметь режимы автономного тестировании. Так, автономный тест принтера запускается без ...
... мероприятия по обеспечению однородности выпускаемой продукции. Все эти мероприятия можно объединить в четыре группы: 1. совершенствование технологии производства; 2. автоматизация производства; 3. технологические (тренировочные) прогоны; 4. статистическое регулирование качества продукции. 2.10. Проектирование технологических процессов с использованием средств ...
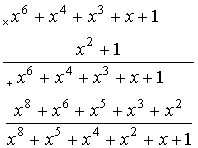
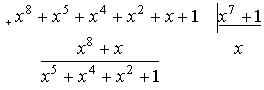
0 комментариев