Принцип максимуму Понтрягіна

3 Принцип максимуму Понтрягіна

Розглянемо задачу оптимального керування (1), (3)–(5):

, , ,

,

, , , ,

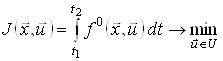де ,  – функції, неперервні за сукупністю всіх змінних і неперервно-диференційовані по змінних .

Перейдемо до -вимірного простору, елементами якого є вектори

,

де  – фазовий вектор задачі, а  – деяка функція, що задовольняє співвідношенню

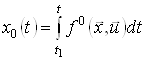.(6)

З останньої формули випливає, що функція  є розв’язком рівняння

.

Приєднавши останнє рівняння до системи (1), дістанемо нову систему

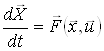,(7)

де ;

.

Підкреслимо, що праві частини рівнянь системи (7) не залежать від . З формули (6) випливає, що

, .

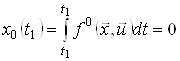Таким чином, початкову задачу зведено до задачі вибору припустимого керування , яке здійснює перехід точки  в -вимірному просторі зі стану  у найближчу точку  на прямій, що паралельна осі , і проходить через точку  (рис. 3). Пошук оптимального керування тепер полягає в мінімізації величини . Дійсно,

.

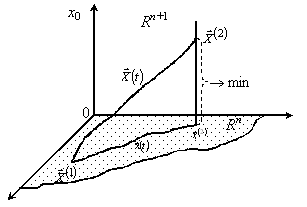
Рисунок 3

Складемо допоміжну систему

, ,(8)

відносно невідомих функцій . Ця система називається спряженою системою до системи (7), а змінні  – спряженими змінними.

Якщо  – припустимий процес, то відповідна цьому процесу система (8) є лінійною однорідною системою диференціальних рівнянь із відомими кусково-неперервними коефіцієнтами. Відомо, що за будь-яких початкових умов ця система має єдиний розв’язок.

Оскільки , , не залежать від , то

,

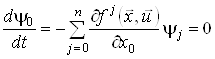і перше рівняння системи (8) можна спростити: , звідки випливає, що .

Розглянемо функцію

,(9)

що називається функцією Понтрягіна, де  – вектор спряжених змінних. Точну верхню грань значень цієї функції по змінній  при фіксованих  і  позначимо через

.

Має місце наступна теорема.

Теорема 1 (принцип максимуму). Якщо керування ,  і відповідна йому фазова траєкторія  оптимальні, то існує така ненульова вектор-функція , що відповідає функціям  і  (тобто задовольняє спряженій системі (8) з функціями  й ), що:

1. Функція  від змінної  набуває максимуму в точці  для будь-якого :

: .

У кінцевий момент часу  має місце співвідношення , .

Умови теореми 1 дозволяють серед усіх траєкторій, що проходять через дві задані точки  й , виділити окремі траєкторії, серед яких перебуває і оптимальна траєкторія, якщо вона існує. Ці умови є необхідними, але не достатніми. Потрібна подальша перевірка знайдених траєкторій на оптимальність. Тільки в найпростішому випадку, коли знайдено лише одну траєкторію, а з деяких міркувань відомо, що оптимальний розв’язок існує, можна стверджувати, що знайдена траєкторія і є оптимальною.

Якщо принципу максимуму задовольняють кілька траєкторій, то для виявлення серед них оптимальної треба застосовувати додаткові умови. Іноді вдається відокремити сторонні траєкторії, порівнюючи значення цільового функціонала. Але оптимальна траєкторія може бути не єдиною, а відкинуті траєкторії, не будучи оптимальними, можуть виявитися локально оптимальними.

Продиференціюємо функцію Понтрягіна (9) за змінними  і :

, ,

, .

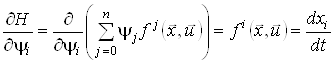Тепер співвідношення (7) і (8) можна переписати у вигляді гамільтонової системи:

.(10)

Якщо , ,  задовольняють системі (10) і умові 1 теореми 1, то функції  і  змінного  є сталими. Умова 2 теореми 1, таким чином, має місце в будь-який момент часу .

4 Принцип максимуму для задачі оптимальної швидкодії

Окремим випадком критерію (5) є критерій

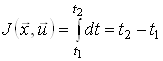,(11)

який називається критерієм оптимальної швидкодії, а відповідна йому задача – задачею оптимальної швидкодії. Оскільки у формулі (11) , то функція Понтрягіна  для задачі оптимальної швидкодії матиме вигляд:

,

де .

Оскільки перший доданок не залежить від , то максимум функції  по  реалізується одночасно з максимумом функції

,

де . Тому далі розглядатимемо нову гамільтонову систему, відкинувши перші рівняння системи (10), що відповідають :

.(12)

Позначимо

.

Можна довести, що

.

З теореми 1 відповідно до умов  і , випливає, що:

1) ;

2) вектор-функції  і  не обертаються в нуль у жодній точці відрізка .

На основі теореми 1 можна сформулювати необхідні умови оптимальності в задачі швидкодії.

Теорема 2. Якщо ,  – оптимальний процес, то існує ненульовий частинний розв’язок  спряженої системи

, ,

 

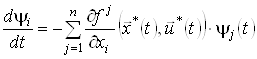такий, що:

1. при кожному значенні  функція  змінної  набуває при  максимального значення:

;

у кінцевий момент часу  має місце співвідношення .

Як і у випадку теореми 1, перевірку умови 2 теореми 2 можна проводити в будь-який момент часу .