Навигация
Программно реализовать на языке C++ метод Свенна
2. Программно реализовать на языке C++ метод Свенна
(Программа должна обеспечить вывод на экран
- начальной точки и шага
на каждой итерации метода:
- номера итерации,
- генерируемой методом новой точки x и значения функции в ней;
а на последней итерации
- отрезка [a, b] локализации минимума функции f(x) и его длины, а также числа итераций.
Метод оценивания точки минимума внутри найденного отрезка локализации минимума
(Программа должна обеспечить на каждой итерации метода вывод на экран:
- номера итерации,
- границ текущего отрезка [a, b],
- внутренних точек и значений функции в них, а затем
- финальной оценки x* точки минимума функции f(x)
- соответствующего точке x* значения функции f(x*)).
3. С помощью программы решить следующие задачи одномерной оптимизации
- f(x) = x2 – 12x. Начальные точки: 1, 3, 0, 10. ∆ = 1, 10
- f(x) = 2x2+(16/x) Начальные точки: 1,6, 2, 1, 0.1, 10. ∆ = 1, 2
- f(x) = (127/4)x2-(61/4)x+2. Начальные точки: 0, 1, 2, -10, 10. ∆= 0,5, 1
4.Составить отчет, содержащий:
- Титульный лист с указанием учебной дисциплины, номера и названия задания, ФИО выполнившего работу студента;
- Полностью текст задания, приведенный несколькими строками выше;
- Определение унимодальности;
- Алгоритмы;
- Текст программы на С++;
- Подробное решение одной из предложенных задач – то, что выводит программа при ее решении на каждой итерации;
- Сводную таблицу результатов решения задач, содержащую информацию о тестовой функции, начальных данных задачи и параметрах программы и результаты решения задачи(оценку точки минимума, значение функции в ней, число итераций).
Задание№1
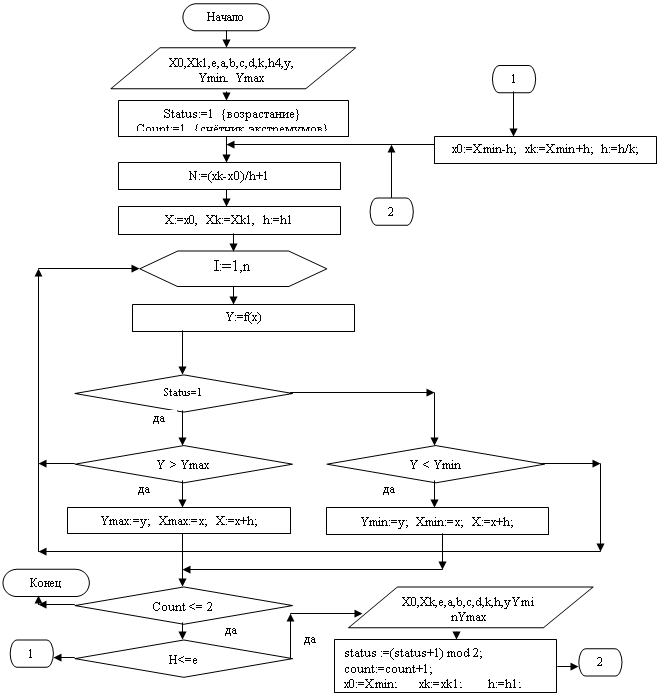
Программно реализовать на языке C++ метод Свенна
(Программа должна обеспечить вывод на экран
- начальной точки и шага на каждой итерации метода:
- номера итерации,
- генерируемой методом новой точки x и значения функции в ней; а на последней итерации отрезка [a, b] локализации минимума функции f(x) и его длины, а также числа итераций.
С помощью программы решить следующие задачи одномерной оптимизации
- f(x) = x2 – 12x. Начальные точки: 1, 3, 0, 10. ∆ = 1, 10
- f(x) = 2x2+(16/x) Начальные точки: 1,6, 2, 1, 0.1, 10. ∆ = 1, 2
- f(x) = (127/4)x2-(61/4)x+2. Начальные точки: 0, 1, 2, -10, 10. ∆= 0,5, 1
Текст программы на С++
#include <iostream.h>
#include <conio.h>
#include <math.h>
#include <iomanip.h>
using namespace std;
double f(double ) ;
int _tmain(int argc, _TCHAR* argv[])
{
double t,ll,e,l,xk,yk,a,b;
double x,delta,xp,x1,x2,k=0,y;
int p=0;
cout<<"enter x* ";
cin>>x ;
cout<<"enter t ";
cin>>t;
x1=x-t;
x2=x+t;
if ((f(x-t) >=f(x)) && (f(x+t) >=f(x)))
{
a=x-t;
b=x+t;
p=1;
};
if ((f(x-t) <=f(x)) && (f(x+t) <=f(x)))
{
p=1;
};
xp=x;
if ((f(x-t) >f(x)) && (f(x) >f(x+t)))
{
delta=t;
a=x ;
x=x+t;
}
if ((f(x-t) < f(x)) && (f(x) < f(x+t)))
{
delta=-t;
b=x ;
x=x-t;
}
while ((p!=1))
{
if ((f(x)< f(xp)) && (delta*t >0))
a=xp;
if ((f(x)< f(xp)) && (delta*t <0))
b=xp;
if ((f(x)> f(xp)) && (delta*t >0))
{
b=x;
p=1;
};
if ((f(x)> f(xp)) && (delta*t<0))
{
a=x;
p=1;
};
k++;
cout<< " Номер итерации "<<k<<endl;
cout<< " Ганицы отрезка a="<<a<<" b="<<b<<endl;
xp=x;
x=xp+pow(2.0,k-1)*delta;
}
cout << " a= "<<a<< " b= "<< b<<endl; cout<< " Количество итераций= " << k<< endl;
system("pause");
return 0;
}
double f(double x)
{
double y;
y=x*x-12*x;
return (y);
}
Решение задачи
Функция f(x) = x2-12x нач. точка x0= 1 шаг 1
Номер итерации 1
Начальная точка 1
X1 = a = 1
F(x) = -11
Номер итерации 2
Начальная точка 1
Шаг 1
X2 = a= 2
F(x) = -20
Номер итерации 3
Начальная точка 2
Шаг 2
X3 = a = 4
F(x) = -32
Номер итерации 4
Начальная точка 4
Шаг 4
X4 = b = 8
F(x) = -32
Отрезок [a;b] =[2;8] Число итераций = 4
Сводная таблица результатов №1
| f(x) = x2-12x | |||
| Начальная точка | Шаг | Отрезок | Число итераций |
| 1 | 1 | [2;8] | 4 |
| 1 | 10 | [-9;11] | 3 |
| 3 | 1 | [4;11] | 4 |
| 3 | 10 | [-7;13] | 3 |
| 0 | 1 | [2;16] | 5 |
| 0 | 10 | [0;30] | 3 |
| 10 | 1 | [2;8] | 4 |
| 10 | 10 | [0;20] | 3 |
Сводная таблица результатов №2
| f(x) = 2x2+(16/x) | |||
| Начальная точка | Шаг | Отрезок | Число итераций |
| 1.6 | 1 | [0.6;2.6] | 3 |
| 1.6 | 2 | [-0.4;3.6] | 3 |
| 2 | 1 | [1;3] | 3 |
| 2 | 2 | [0;2] | 3 |
| 0.1 | 1 | [-0.9;2.1] | 3 |
| 0.1 | 2 | [-1.9;4.1] | 3 |
| 10 | 1 | [-5;9] | 4 |
| 10 | 2 | [-4;8] | 3 |
Сводная таблица результатов №3
| f(x) = (127/4)x2-(61/4)x+2 | |||
| Начальная точка | Шаг | Отрезок | Число итераций |
| 0 | 0.5 | [-0.5;0.5] | 2 |
| 0 | 1 | [-1;1] | 2 |
| 1 | 0.5 | [-1;0.5] | 3 |
| 1 | 1 | [-1;1] | 2 |
| 2 | 0.5 | [-2;1] | 4 |
| 2 | 1 | [-2;1] | 3 |
| -10 | 0.5 | [-6;6] | 6 |
| -10 | 1 | [-6;6] | 5 |
| 10 | 0.5 | [-6;6] | 6 |
| 10 | 1 | [-6;6] | 5 |
Задание №2
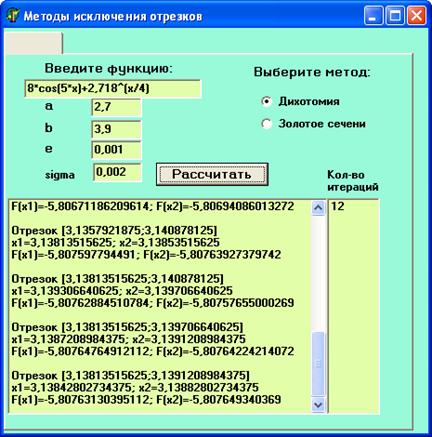
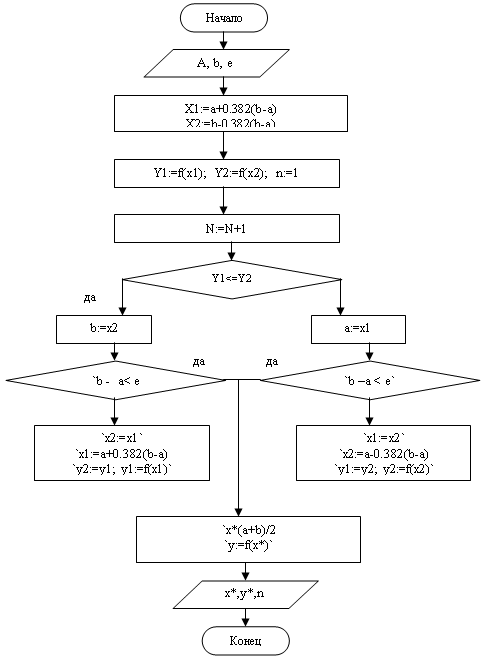
Найти точки минимума внутри найденного отрезка локализации минимума методом золотого сечения.
(Программа должна обеспечить на каждой итерации метода вывод на экран:
- номера итерации,
- границ текущего отрезка [a, b],
- внутренних точек и значений функции в них,
а затем
- финальной оценки x* точки минимума функции f(x)
- соответствующего точке x* значения функции f(x*)).
Текст программы на С++
#include <iostream.h>
#include <iomanip.h>
#include <math.h>
#include <conio.h>
#include <stdlib.h>
double function (double); // вычисляет значение функции в данной точке
void main (void)
{
double a, b, E, F1, F2, LM, x = 0, fc, fd, fx, i = 0, c = 0, d = 0; // Определение переменных
clrscr();
cout << "Введите границы начального отрезка:" << endl << "a0 = ";
cin >> a;
cout << "b0 = ";
cin >> b;
cout << "Введите число Е:" << endl << "E = ";
cin >> E;
clrscr();
cout << "Границы начальнога отрезка:"<< endl <<"а[" << i << "] = " << a << endl;
cout << "b[" << i << "] = " << b << endl;
cout << "Число Е = " << E << endl;
F1 = (3 - sqrt(5))*0.5;
F2 = 1 - F1;
do
{
LM = b - a;
cout << endl << "Номер итерации " << i + 1 << endl;
cout << "Границы текущего отрезка:" << endl << "а[" << i << "] = " << a << endl;
cout << "b[" << i << "] = " << b << endl;
if (LM <= E)
{
x = (a + b)*0.5;
fx = function(x);
cout << "Точка минимума x = " << setprecision(10) << x << endl;
cout << "Значение функции F(x) в точке минимума = " << setprecision(10) << fx << endl;
cout << "Press any key";
getch();
exit(0);
}
else
{
c = a + F1 * LM;
d = a + F2 * LM;
fc = function(c);
fd = function(d);
cout << "Значение внутренней точки с[" << i << "] = " << setprecision(10) << c << endl;
cout << "Значение внутренней точки d[" << i << "] = " << setprecision(10) << d << endl;
cout << "Значение функции F(x) в точке с[" << i << "] = " << setprecision(10) << fc << endl;
cout << "Значение функции F(x) в точке d[" << i << "] = " << setprecision(10) << fd << endl;
}
if (fc == fd)
{
a = c;
b = d;
x = (a + b)*0.5;
fx = function(x);
cout << "Точка минимума x = " << setprecision(10) << x << endl;
cout << "Значение функции F(x) в точке минимума = " << setprecision(10) << fx << endl;
cout << "Press any key";
getch();
exit(0);
}
else
{
if (fc < fd)
{
a = a;
b = d;
i++;
}
else
{
a = c;
b = b;
i++;
}
}
}
while (1);
}
double function (double x)
{
double y;
y = x * x - 12 * x;
return (y);
}
Решение задачи
Функция f(x) = x2-12x
Границы начального отрезка:
а[0] = -9
b[0] = 11
Число Е = 0.1
Номер итерации 1
Границы текущего отрезка:
а[0] = -9
b[0] = 11
Значение внутренней точки с[0] = -1.36
Значение внутренней точки d[0] = 3.36
Значение функции F(x) в точке с[0] = 18.17
Значение функции F(x) в точке d[0] = -29.03
Номер итерации 2
Границы текущего отрезка:
а[1] = -1.36
b[1] = 11
Значение внутренней точки с[1] = 3.36
Значение внутренней точки d[1] = 6.27
Значение функции F(x) в точке с[1] = -29.03
Значение функции F(x) в точке d[1] = -35.92
Номер итерации 3
Границы текущего отрезка:
а[2] = 3.36
b[2] = 11
Значение внутренней точки с[2] = 6.27
Значение внутренней точки d[2] = 8.08
Значение функции F(x) в точке с[2] = -35.92
Значение функции F(x) в точке d[2] = -31.66
Номер итерации 4
Границы текущего отрезка:
а[3] = 3.36
b[3] = 8.08
Значение внутренней точки с[3] = 5.16
Значение внутренней точки d[3] = 6.27
Значение функции F(x) в точке с[3] = -35.3
Значение функции F(x) в точке d[3] = -35.92
Номер итерации 5
Границы текущего отрезка:
а[4] = 5.16
b[4] = 8.08
Значение внутренней точки с[4] = 6.27
Значение внутренней точки d[4] = 6.96
Значение функции F(x) в точке с[4] = -35.92
Значение функции F(x) в точке d[4] = -35.06
Номер итерации 6
Границы текущего отрезка:
а[5] = 5.16
b[5] = 6.96
Значение внутренней точки с[5] = 5.85
Значение внутренней точки d[5] = 6.27
Значение функции F(x) в точке с[5] = -35.97
Значение функции F(x) в точке d[5] = -35.92
Номер итерации 7
Границы текущего отрезка:
а[6] = 5.16
b[6] = 6.27
Значение внутренней точки с[6] = 5.58
Значение внутренней точки d[6] = 5.85
Значение функции F(x) в точке с[6] = -35.83
Значение функции F(x) в точке d[6] = -35.97
Номер итерации 8
Границы текущего отрезка:
а[7] = 5.58
b[7] = 6.27
Значение внутренней точки с[7] = 5.85
Значение внутренней точки d[7] = 6.01
Значение функции F(x) в точке с[7] = -35.97
Значение функции F(x) в точке d[7] = -35.99
Номер итерации 9
Границы текущего отрезка:
а[8] = 5.85
b[8] = 6.27
Значение внутренней точки с[8] = 6.01
Значение внутренней точки d[8] = 6.11
Значение функции F(x) в точке с[8] = -35.999
Значение функции F(x) в точке d[8] = -35.986
Номер итерации 10
Границы текущего отрезка:
а[9] = 5.85
b[9] = 6.11
Значение внутренней точки с[9] = 5.95
Значение внутренней точки d[9] = 6.01
Значение функции F(x) в точке с[9] = -35.997
Значение функции F(x) в точке d[9] = -35.999
Номер итерации 11
Границы текущего отрезка:
а[10] = 5.95
b[10] = 6.11
Значение внутренней точки с[10] = 6.01
Значение внутренней точки d[10] = 6.05
Значение функции F(x) в точке с[10] = -35.999
Значение функции F(x) в точке d[10] = -35.997
Номер итерации 12
Границы текущего отрезка:
а[11] = 5.95
b[11] = 6.05
Значение внутренней точки с[11] = 5.99
Значение внутренней точки d[11] = 6.01
Значение функции F(x) в точке с[11] = -35.999
Значение функции F(x) в точке d[11] = -35.999
Номер итерации 13
Границы текущего отрезка:
а[12] = 5.95
b[12] = 6.01
Точка минимума x = 5.981
Значение функции F(x) в точке минимума = -35.999999
| f(x) = x2-12x | ||||
| | отрезки | Точка минимума | Значение функции | Число итераций |
| 0.1 | [2;8] | 6.003 | -35.999999 | 10 |
| [-9;11] | 5.981 | -35.999999 | 13 | |
| [4;11] | 5.996 | -35.999999 | 10 | |
| [-7;13] | 6.018 | -35.999966 | 13 | |
| [2;16] | 6.006 | -35.999957 | 12 | |
| [0;30] | 6.002 | -35.999997 | 13 | |
| [2;8] | 6.003 | -35.999999 | 10 | |
| [0;20] | 6.005 | -35.999965 | 13 | |
| f(x) = 2x2+(16/x) | ||||
| | отрезки | Точка минимума | Значение функции | Число итераций |
| 0.01 | [0.6;2.6] | 1.5875 | 15.119055 | 13 |
| [-0.4;3.6] | 1.5820 | 15.119055 | 15 | |
| [1;3] | 1.5861 | 15.119055 | 14 | |
| [0;2] | 1.5874 | 15.119052 | 13 | |
| [-0.9;2.1] | 1.5880 | 15.119050 | 13 | |
| [-1.9;4.1] | 1.5864 | 15.119057 | 15 | |
| [-5;9] | 1.5862 | 15.119061 | 17 | |
| [-4;8] | 1.5866 | 15.119055 | 16 | |
| f(x) = (127/4)x2 - (61/4)x+2 | ||||
| | Отрезки | Точка минимума | Значение функции | Число итераций |
| 0.001 | [-0.5;0.5] | 0.2418 | 0.18548 | 16 |
| [-1;1] | 0.2418 | 0.18548 | 17 | |
| [-1;0.5] | 0.2420 | 0.18548 | 17 | |
| [-1;1] | 0.2418 | 0.18548 | 17 | |
| [-2;1] | 0.2420 | 0.18548 | 18 | |
| [-2;1] | 0.2420 | 0.18548 | 18 | |
| [-6;6] | 0.2418 | 0.18548 | 21 | |
| [-6;6] | 0.2418 | 0.18548 | 21 | |
| [-6;6] | 0.2418 | 0.18548 | 21 | |
| [-6;6] | 0.2418 | 0.18548 | 21 | |
Похожие работы
... Метод преобразования целевой функции, метод штрафных функций, табличный симплекс – метод. Список используемой литературы 1. А.Г.Трифонов. Постановка задачи оптимизации и численные методы ее решения; 2. Б. Банди. Методы оптимизации. Вводный курс., 1988; 3. Мендикенов К.К. Лекции Приложение А using System; using System.Collections.Generic; using System.ComponentModel; using System. ...
... исследованных функций. Так же необходимо изучить работу встроенных в MatLab функций. Протестировать программу на серии тестов. Теоретическое описание Одномерная оптимизация функций методом золотого сечения Метод золотого сечения состоит в построении последовательности отрезков [a0, b0], [a1, b1], …,стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление ...
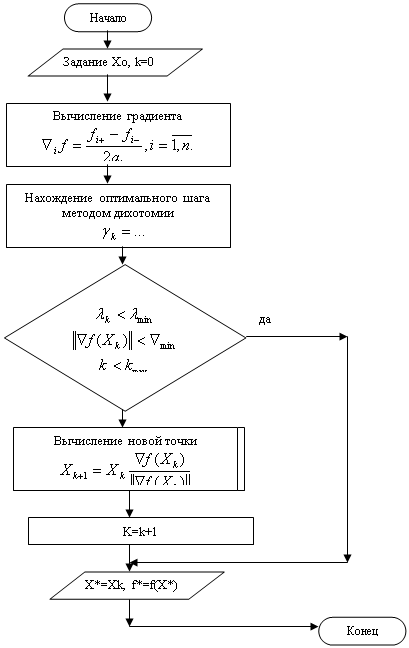
... : т.е. . Для определения координат точки Х1 нужно выбрать значение шага . Получим : Из соотношения (,)=0 имеем: (-3-3)(-3)+(1+)=10+10=0 откуда = Задание 4 ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом. ...
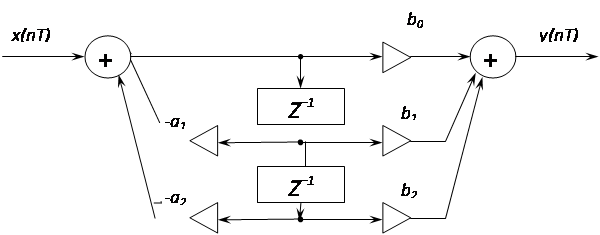
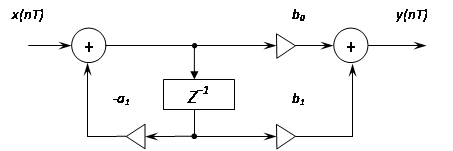
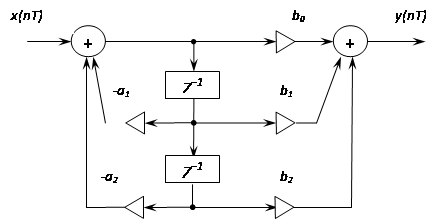
... звеньев первого и второго порядка представлена на следующем рисунке: 3. Методы расчета БИХ-фильтров и вид целевой функции Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях. ...
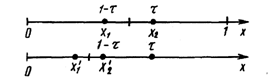

0 комментариев