Визначення закону зміни зовнішнього моменту, що забезпечує сталість кутової швидкості

3.2 Визначення закону зміни зовнішнього моменту, що забезпечує сталість кутової швидкості

При дії зовнішнього моменту , що забезпечує рівномірне обертання механічної системи навколо шарніра , остання доданок у лівій частині рівності (3.1.9) звертається в нуль:

, ; звідси .

Тоді вираження (3.1.9) прийме вид:

 (3.2.1)

 спрямований протилежно головному моменту зовнішніх сил, тобто, проти годинникової стрілки.

Зовнішній момент, що забезпечує рівномірне обертання конструкції, дорівнює:

 (3.2.2)

4. Визначення реакцій в опорах обертового тіла

Визначимо реакції в опорі обертового тіла методом кінетостатики. Він полягає в рішенні задачі динаміки засобами (рівняннями) статики. Для кожної крапки механічної системи справедливо основне рівняння динаміки:

 (4.1)

Тут  і  – маса й прискорення деякої крапки системи;  – сума всіх активних сил і реакцій зв'язків, прикладених до неї.

Основному рівнянню динаміки (4.1) можна додати вид рівняння статики:

 (4.2)

Тут  – сила інерції крапки механічної системи.

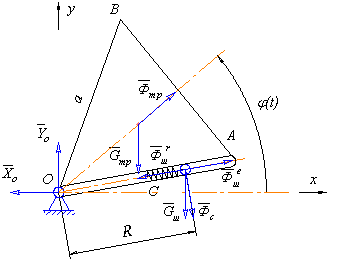
Малюнок 4.1. Визначення реакцій в опорах обертового тіла

Для заданої механічної системи рівняння статики (4.2) має вигляд:

 (4.3)

Для визначення реакції шарніра нам необхідно й досить взяти за координатні осі – нерухливі осі  й , і визначити тридцятимільйонні реакції шарніра на ці осі:

 (4.4)

Звідси:

Підставивши значення сил, одержимо:

 (4.5)

Тепер проектуємо (4.2) на нерухливу вісь :

 (4.6)

Звідси:

Підставивши відомі значення сил, одержимо:

 (4.7)

Повну реакцію в шарнірі  можна знайти по формулі: , де  й  визначаються вираженнями (4.5) і (4.7);

5. Дослідження руху механічної системи із двома ступенями волі за допомогою рівнянь Лагранжа II роду

5.1 Складання рівнянь руху системи методом Лагранжа

Рівняння другого роду є одним з найбільш зручних прийомів складання рівнянь руху механічних систем. Вони мають такий вигляд:

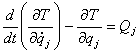
  (5.1.1)

Тут  – кінетична енергія системи; , , , – узагальнені координати, швидкості й сили відповідно;  – число ступенів волі.

Рівняння (5.1.1) утворять систему  рівнянь другого порядку щодо  функцій , а порядок даної системи дорівнює . Форма рівнянь Лагранжа не залежить від вибору узагальнених координат . У зв'язку із цим говорять, що рівняння Лагранжа другого роду мають властивість інваріантності.

Як видно з (5.1.1), для одержання рівнянь Лагранжа необхідно знайти відповідні похідні від кінетичної енергії системи й визначити узагальнені сили.

Визначимо кінетичну енергію системи. Вона буде складатися з кінетичних енергій трикутника й кульки: .

Підставивши значення  з (3.1.5), одержимо:

 (5.1.2)

Кінетична енергія кульки визначається його масою й відносною й переносною швидкостями:

З урахуванням відомих значень швидкостей, одержимо:

 (5.1.3)

Кінетична енергія системи дорівнює:

 (5.1.4)

Знайдемо похідні від кінетичної енергії згідно (5.1.1):

 (5.1.5) (5.1.6)

 (5.1.7) (5.1.8)

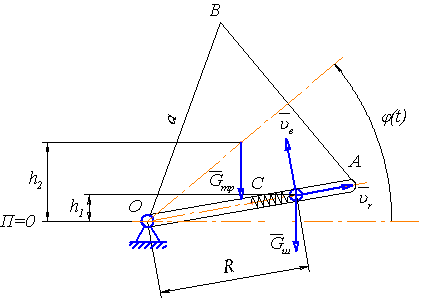
Малюнок 5.1.1. Визначення кінетичної й потенційної енергій системи

Тепер, виходячи з (5.1.1), потрібно визначити узагальнені сили. Дана механічна система є консервативної, ми можемо визначити узагальнені сили через потенційну енергію по формулі:

 (5.1.9)

Знайдемо потенційну енергію. Вона буде складатися з робіт консервативних сил по переміщенню тіла з нульового положення: . За нульовий рівень потенційної енергії виберемо початковий момент часу, при :

 – енергія положення кульки;

 – енергія положення прямокутника;

 – потенційна енергія сили пружності;

Потенційна енергія системи дорівнює:

 (5.1.10)

Знайдемо узагальнені сили:

 (5.1.11)

 (5.1.12)

Тепер можемо записати систему рівнянь Лагранжа II роду:

 (5.1.13)

 (5.1.14)