Навигация
Линейные электрические цепи постоянного и синусоидального тока
Курсовая работа
«Линейные электрические цепи постоянного и синусоидального тока»
Задания
Цель работы: Расчёт и исследование цепей постоянного и синусоидального тока. Определить: 1) токи всех ветвей схемы, используя МКТ, МУП. 2) ток в выделенной ветви, используя МЭГi, МЭГu. 3) проверить баланс мощностей 4) привести схемы в EWB или Ms для измерения токов ветвей, напряжений на элементах.Задание 1
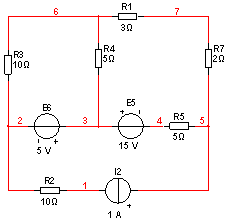
Дано:
R1 = 3 Ом, R2 = 10 Ом, R4 = 10 Ом, R5 = 5 Ом, R7 = 2 Ом,
J2 = 1A, E5 = 20B, E6 = 5B.
Задание 2
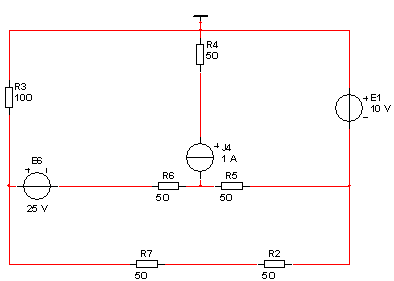
Дано:
R2 = 5 Ом, R3 = 10 Ом, R4 = 5 Ом, R5 = 5 Ом, R6 = 5 Ом, R7 = 5 Ом,
J4 = 1 A, E1 = 10 B, E6 = 25 B.
Задача 3
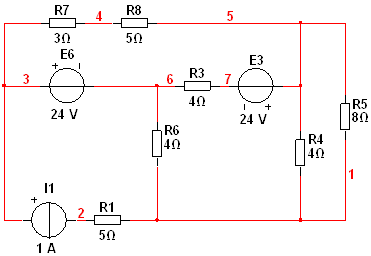
Дано:
R1 = 6 Ом, R2 = 3 Ом, R4 = 10 Ом, R5 = 1 Ом, R6 = 3 Ом, R7 = 3 Ом, R8 = 6 Ом,
J2 = 1 A, E3 = 12 B, E4 = 24 B.
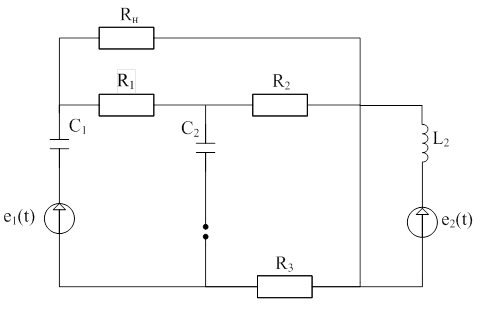
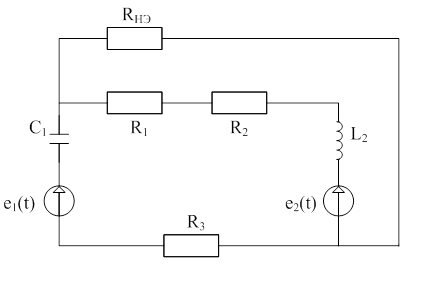
Задание 4
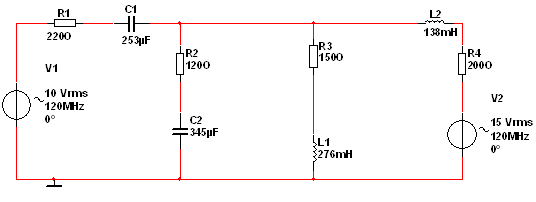
Дано:
R1 = 220 Ом, R2 = 120 Ом, R3 = 150 Ом, R4 = 200 Ом, E1 = 10B, E3 = 15B,
f = 120МГц, C1 = 253 мкФ, C2 = 345 мкФ, L1 = 276 мГн, L2 = 138 мГн.
Линейные электрические цепи постоянного тока
Теория, метод контурных токов
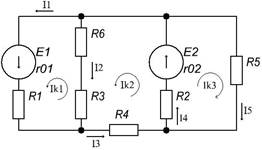
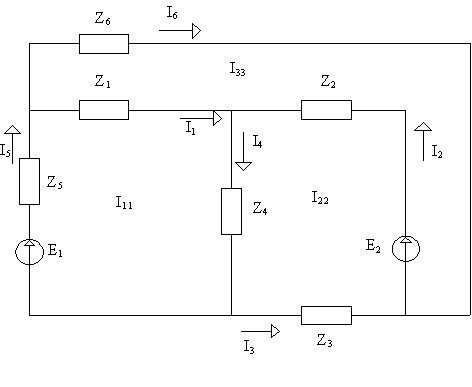
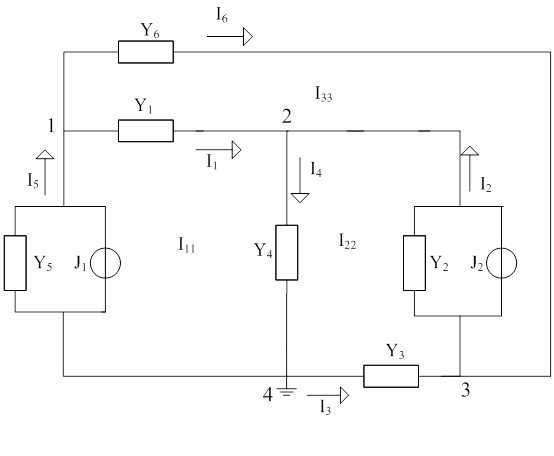
Нам дана линейная электрическая цепь. Задача, заключается в нахождении сначала контурных токов, затем и токов в ветвях. Сначала выбираем произвольно направления токов в контурах, его можно выбрать по часовой стрелке и против часовой стрелки, но это условно, так как исходя из полученного в дальнейшем знака, мы будем судить о направлении тока. Воспользуемся фундаментальными законами Кирхгофа. В частности первый закон Кирхгофа: алгебраическая сумма токов, подтекающих к любому узлу схемы, равна 0. Применив закон к примеру (рис. 1) получаем систему уравнений:
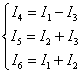 .
.
Выбираем дерево, которое включает в себя максимальное количество ветвей без источников тока. Пусть это будут ветви, содержащие ![]() . Затем выбираем контура, и выбираем обход контура. Воспользуемся вторым законом Кирхгофа: алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура. Для выбранных нами контуров составляем систему уравнений Кирхгофа:
. Затем выбираем контура, и выбираем обход контура. Воспользуемся вторым законом Кирхгофа: алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура. Для выбранных нами контуров составляем систему уравнений Кирхгофа:
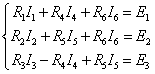
Возьмем токи из первого закона Кирхгофа и подставим их в уравнения из второго закона Кирхгофа. Получим:
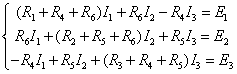
Поясним данную систему. Через каждый элемент протекает некоторый контурный ток: ![]()
![]()
![]() . Значит падение напряжения на элементе обусловлено протеканием через него всех контурных токов, причем напряжение от собственного контурного тока всегда берется со знаком плюс. Падения напряжений от остальных контурных токов берутся со знаком плюс, если направления контурных токов совпадает с направлением рассматриваемого тока, и в обратном случае с минусом.
. Значит падение напряжения на элементе обусловлено протеканием через него всех контурных токов, причем напряжение от собственного контурного тока всегда берется со знаком плюс. Падения напряжений от остальных контурных токов берутся со знаком плюс, если направления контурных токов совпадает с направлением рассматриваемого тока, и в обратном случае с минусом.
Затем записываем матрицу сопротивлений симметричную относительно главной диагонали. В правой части мы записываем сумму ЭДС входящих в контур если направление ЭДС совпадает с направлением обхода контура, то она со знаком «+», в противном случае – со знаком минус. При переходе от токов ветвей к контурным токам первый закон Кирхгофа выполняется всегда.
Определяем количество уравнений МКТ, по формуле:
![]() (где N-число (узлов, ветвей, уравнений))
(где N-число (узлов, ветвей, уравнений))
Если в цепи присутствуют независимые источники тока, то число уравнений уменьшается на количество источников токов:
![]() . (где Nj – число источников тока)
. (где Nj – число источников тока)
Записываем уравнения МКТ в общем виде:
![]()
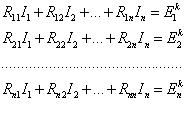 ,
,
Получаем матричное уравнение по МКТ.
Запишем алгоритм записи уравнений по МКТ:
1) чертится граф;
2) выбирается дерево;
3) выбираются независимые контуры путем добавления хорд к ветвям дерева;
4) выбираются направления контуров;
5) записываются уравнения по методу контурных токов числом, указанным выше;
6) определяются контурные токи (решается система уравнений);
7) определяются токи во всех ветвях; обратим внимание на то, что через каждую хорду будет протекать только контурный ток:
![]() но
но ![]() .
.
Получим систему уравнений МКТ формально. Воспользуемся стандартной ветвью.
![]()
![]()
![]()
![]()
![]()

Вспоминаем, что токи ветвей связаны с токами хорд следующим соотношением: ![]() , откуда становится ясно, что наши контурные токи – это и есть
, откуда становится ясно, что наши контурные токи – это и есть ![]() . Далее,
. Далее,
![]()
Система была неполная, но мы сменили базис и перешли к полной системе.
![]()
![]()
Отсюда можно определить:
![]()
![]()
![]()
![]()
Уравнение ![]() и есть формальное уравнение записи по МКТ. Здесь действительно учтены как независимые источники ЭДС, так и независимые источники тока. Количество уравнение получается автоматически. Также из уравнения
и есть формальное уравнение записи по МКТ. Здесь действительно учтены как независимые источники ЭДС, так и независимые источники тока. Количество уравнение получается автоматически. Также из уравнения ![]() становится ясно, что формальная запись
становится ясно, что формальная запись ![]() и
и ![]() выглядит следующим образом:
выглядит следующим образом:
![]()
![]() .
.
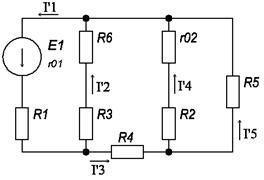
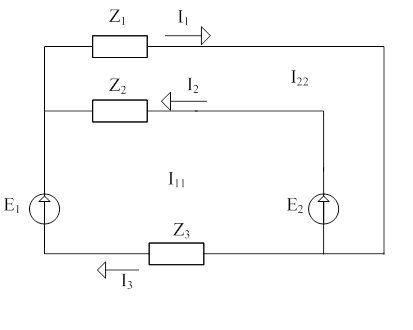
Задание 1
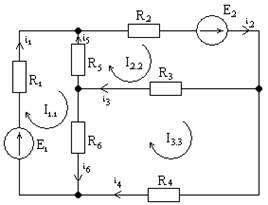
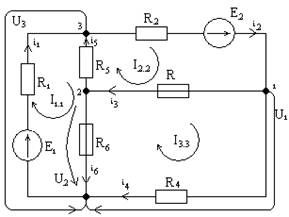
Принципиальная схема цепи выглядит следующим образом:
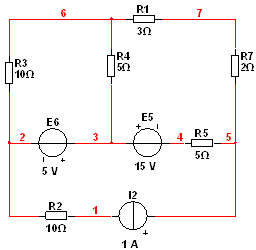
Найдем количество уравнений. Так как в цепи присутствуют независимые источники тока, то мы имеем:
![]()
![]()
Теперь выберем независимые контуры. Пусть первый контур состоит из ветвей 1, 4, 5, и по нему течет ток I11 по часовой стрелке. Пусть второй контур состоит из ветвей 2, 4, 6, по нему течет ток I22 по часовой стрелке.
Запишем систему уравнений по методу контурных токов:
![]()
(R3+R4)*I11-R4*I22=-E6
(R1+R7+R4+R5)*I22-I11*R4 – J1*R5=E5
![]() 15 * I11 – 5 * I22 = -5,
15 * I11 – 5 * I22 = -5,
-5 * I11 + 15 * I22 = 15;
Решим систему по методу Крамера. Найдем определители:
D = 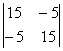 = 200, D22 =
= 200, D22 = 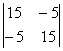 = 200, D11 =
= 200, D11 = 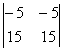 = 0.
= 0.
Найдем контурные токи:
I11 = D11/D = 0 A; I22 = D22/D = 1 A
Теперь посчитаем токи во всех ветвях.
Через хорды текут только контурные токи, поэтому:
I3 = I22 = 0 A
I1 = I11 = 1 A
В ветви с источником тока течет ток, создаваемый этим источником:
I2 = J1 = 1A
Токи в остальных ветвях найдем как сумму контурных токов, текущих по ним, с учетом знаков:
I4 = I22 – I11 = 1 A
I6 = J1-I11 = -1 A
I5 = I22 + J1 = 2 A
Проверка
1) Балланс мощностей:
E5*I5 + E6*I6 +J2*(U2+I2*R2) = I1^2*R1+I2^2*R2+I3^2*R3+I4^2*R4+I5^2*R5+I1^2*R7
Похожие работы
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат – потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис. 1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...
... – 0,1 + 0,03 + 0,191 = 0,12 ί3 – ί6 – ί5 = – 0,1 – 0,11 + 0,11 = – 0,11 ί6 + ί4 – ί1 = 0,11 – 0,01 – 0,03 = 0,07 ί2 – ί3 – ί4 = – 0,19 + 0,1 + 0,01 = – 0,08 ЗАДАЧА 2 Линейные электрические цепи синусоидального тока В сеть переменного тока с действующим значением напряжения U включена цепь, состоящая из двух параллельных ветвей. Определить ...
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...
... ветви равно разности узловых потенциалов на концах этой ветви, а произведение этого напряжения на проводимости ветви равного проходящему через неё току. 1.2.2 Расчет электрической цепи методом узловых потенциалов Схеме в соответствии с рисунком 2, заменяется на эквивалентность. Вместо комплексных сопротивлений используется комплексные проводимости, а источники напряжения заменяется источниками ...

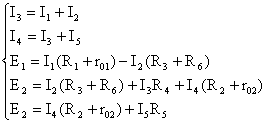


0 комментариев