Навигация
Задачі сигналів та критерії оптимальності рішень
14685
знаков
0
таблиц
2
изображения
Задачі обробки сигналів та критерії оптимальності рішень
1. Класифікація задач обробки сигналів
Існують різні типи задач обробки сигналів, серед яких основними є наступні.
Виявлення сигналу на фоні завад. У цій задачі обробки сигналів необхідно прийняти одну з двох гіпотез – діє тільки завада або сигнал з завадою:
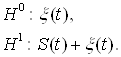
Задача розрізнення заданих сигналів. У цій задачі обробки сигналів необхідно прийняти одну з 
гіпотез про дію одного із заданих сигналів на фоні завади:
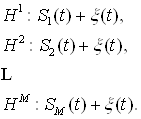
Задача оцінювання параметрів сигналів. У цій задачі обробки сигналів за сумішшю сигналу з завадою 
необхідно прийняти рішення про те, яке значення приймає параметр 
сигналу 
. При цьому припускається, що на інтервалі часу спостереження сигналу 
параметр не змінюється:
Задача фільтрації сигналів. У цій задачі обробки сигналів із суміші сигналу з завадою 
необхідно виділити параметр сигналу 
. Припускається, що на інтервалі часу спостереження сигналу повідомлення змінюється у часі. Частинним випадком є задача виділення (фільтрування) сигналу 
із суміші з шумом 
.
Зустрічаються також комбіновані задачі обробки сигналів, зокрема, сумісного виявлення (чи розрізнювання) та оцінювання параметрів сигналів.
При вирішенні вказаних задач обробки сигналів припускається відомою інформація про вид корисного сигналу та статичні характеристики завади (щільність ймовірності розподілу, кореляційна функція, математичне сподівання, дисперсія та ін.). Окрім того вважається заданим критерій оптимальності вирішення задачі обробки сигналів. Оскільки сигнали, що поступають на вхід приймального пристрою, носять випадковий характер, то при отриманні оптимальних методів обробки сигналів необхідно використовувати основні положення математичної статистики та теорії прийняття статистичних рішень. Математична статистика одержує певні висновки з експериментальних даних. Тому припускається, що відома реалізація прийнятого сигналу, яка використовується безпосередньо або у вигляді деяких її відліків.
Серед задач статистичного синтезу найважливішими для теорії обробки сигналів є такі: перевірка статистичних гіпотез (коли відносно характеристик розподілу ймовірностей висуваються несумісні гіпотези 
і за вектором спостережень вибирається одна з них), оцінювання параметрів розподілу, фільтрування повідомлення з прийнятої реалізації сигналу.
У задачах перевірки гіпотез 
прийняття рішення геометрично означає розбиття простору спостережень на 
-ну область, що не перетинаються:
,
. (1)
У цій задачі 
-те рішення приймається, коли вектор спостережень потрапляє в область
.
При оцінюванні параметра розподілу за спостереженням 
з простору 
знаходиться оцінка параметра 
, що належить простору параметрів 
. У задачах фільтрування за прийнятою реалізацією 
знаходиться оцінка 
переданого повідомлення з простору
.
У математичній статистиці, крім простору спостережень та функції правдоподібності 
до апріорної інформації слід додати так звану функцію втрат, яка характеризується для кожної пари; прийняте рішення – істинне твердження. Для задач перевірки гіпотез 
– це матриця втрат 
, для задач оцінювання параметрів – функція втрат 
. Функція втрат означає «платню» за вибирання гіпотези 
, коли істинна гіпотеза 
. Невід’ємна функція означає „платню” за вибирання оцінки , коли істинне значення параметра дорівнює 
.
Для того, щоб порівняти рішення, у математичній статистиці вибирають ті чи інші показники якості – критерії якості правил вибору рішень. Останні називають також алгоритмами обробки спостережень. Спинимося на особливостях критеріїв у задачах перевірки гіпотез, оцінювання параметрів і фільтрування повідомлень.
Залежно від того, яка у дослідника є апріорна інформація, вибираються ті чи інші показники якості вирішення задачі обробки сигналів.
Похожие работы
... груп за визначений період часу. За допомогою цих даних (статистичної вибірки) ми зможемо описати закон розподілу попиту, на основі якого в подальшому буде ґрунтуватись оптимальне використання складських приміщень. Масштабування даних – переведення з одиниць виміру «пляшки» в «ящики» для зручності розрахунків. Обчислення середніх значень попиту на товари за період та окремо по кожному виду. ...
... знаходження оптимального оператора системи. Параметрична оптимізація, тобто вибір оптимальних значень параметрів системи при заданій її структурі. 3. Дискретний вибір оптимальних варіантів системи із скінченного числа допустимих варіантів. Математичні методи оптимізації параметрів і дискретного вибору добре розвинуті й широко використовуються при проектуванні систем. Синтез структури системи є ...
... замінено на /2. Покладемо ,, k=k+1, j=1 та повернемося до першого кроку. Блок-схема алгоритму приведена нижче. Рисунок 2.4–Алгоритм Хука-Дживса 3. Розробка програмного забезпечення вирішення задачі формування портфеля цінних паперів 3.1 Загальні відомості про програмне забезпечення Розроблене програмне забезпечення призначене для автоматизації процесу формування портфелем цінних ...
... , визначення основних характеристик одноканальних систем масового обслуговування вимагає великої обчислювальної роботи, в зв’язку з чим всі розрахунки робляться на комп’ютері. 1.2 Побудова моделей задач масового обслуговування (на прикладі роботи обчислювального центру (ОЦ)) 1.2.1 Модель для імітації виробничої діяльності ОЦ 1.2.1.1 Завдання Розробити модель для імітації виробничої ді ...
0 комментариев