Критерії оптимальності в задачі оцінювання параметрів

4. Критерії оптимальності в задачі оцінювання параметрів

Критерії оптимальності в задачі оцінювання параметрів розподілів ймовірностей мають деякі відмінності порівняно із задачею перевірки гіпотез. Різниця у тому, що параметр функції правдоподібності  у задачах вибору гіпотез має дискретний характер (і значення параметра ототожнюється з гіпотезами), а в задачах оцінювання параметрів він звичайно набирає значення з континуальної множини. Це відбивається як на вигляді показників (критеріїв) якості рішення, так і на вигляді критеріїв оптимальності. Спинимося на них.

Показник середнього ризику. Середній ризик – це середнє значення функції втрат:

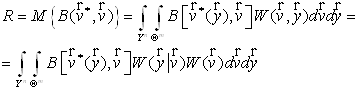 (13)

Тут припускається, що вимірність вектора параметрів  у загальному випадку не збігається з вимірністю вектора спостережень .

Показник середньоквадратичної похибки. В окремому випадку квадратичної функції втрат середній ризик приводить до середньоквадратичної похибки оцінювання скалярного параметра

. (14)

Величина цієї похибки і використовується як показник якості рішення.

Показник апостеріорної щільності ймовірності. Для завдання цього показника (критерію) якості використовують відповідну формулу Байєса:

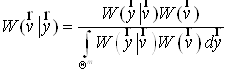. (15)

Наведені показники (критерії) якості дають змогу ввести відповідні критерії оптимальності рішень.

Байєсівський критерій оптимальності. Аналогічно (6), байєсівський критерій оптимальності характеризується умовою мінімізації середнього ризику (13):

. (16)

Враховуючи, що

,

співвідношення (16) можна записати так:

.

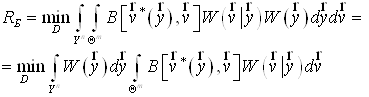У теорії оцінювання параметрів доводиться, що оцінка, яка мінімізує функціонал

,

мінімізує також і середній ризик , що має назву апостеріорного ризику.

Критерій мінімізації середньоквадратичної похибки. Тут вимагається мінімізація величини похибки :

. (17)

 

Критерій максимуму апостеріорної щільності ймовірності. У задачі оцінювання параметрів цей критерій набирає такого вигляду:

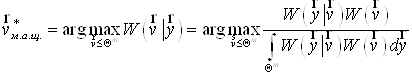. (18)

Оцінка  має назву оцінки максимальної апостеріорної щільності ймовірності оцінювання параметра.

Аналогічно задачі вибору гіпотез можна розглядати мінімаксний критерій, критерій максимальної правдоподібності та інші.

Критерій максимальної правдоподібності. Показником якості рішення може бути функція правдоподібності, а критерієм оптимальності – вимога максимізації цієї функції:

. (19)

У теорії оцінювання параметрів розподілів важливі якісні характеристики одержуваних оцінок, основним з яких є: незсуненість, ефективність, обґрунтованість.

Оцінка, математичне сподівання якої за будь-якого значення параметра збігається з істинним значенням параметра

, (20)

називається незсуненою.

Нагадаємо, що оцінка – це функція спостереження . На множині спостережень  задана імовірнісна міра і тому можна розглядати одержувану оцінку  як реалізацію випадкової величини . Тому для математичного сподівання цієї випадкової величини має місце співвідношення (20).

Для порівняння різних оцінок вводять ту чи іншу міру розкиду. Так, для скалярного параметра використовують другий момент . Якщо оцінка незсунена, ця величина збігається з дисперсією .

Оцінка  більш ефективна порівняно з оцінкою , якщо .

Введемо нижню границю

. (21)

Нарешті, оцінка  параметра  називається обґрунтованою, якщо за умови  вона збігається за ймовірністю з , тобто якщо

. (22)

5. Критерії оптимальності в задачі фільтрування повідомлень

У теорії зв’зку розглядаються особливості передавння різних повідомлень (дискретних, аналогових) різними методами. При передаванні дискретних чи аналогових повідомлень з використанням цифрових і дискретних методів модуляції задачі приймання сигналів можна розв’язувати методами теорії перевірки гіпотез та оцінювання параметрів. Проте у загальному випадку передавання аналогових повідомлень з використанням аналогових методів модуляції цих методів недостатньо. Необхідно використовувати більш спеціальні методи – методи фільтрування повідомлень.

Згідно з узагальненим рівнянням зв’язку, прийнятий сигнал  описується операторним рівнянням

, (23)

де передане повідомлення – , переданий сигнал – , завада –. Залежно від методів модуляції та завадових умов залежність прийнятого сигналу від переданого повідомлення може бути різною. У лінійних методах модуляції (АМ, ОМ, БМ), в умовах адитивних завад можна розглядати найпростішу задачу адитивної взаємодії  та:

. (23а)

У нелінійних методах модуляції (ЧМ, ФМ, деякі імпульсні методи модуляції) за необхідністю ця залежність більш складна.

Задача фільтрування полягає у тому, що за прийнятою реалізацією сигналу  необхідно знайти оцінку  реалізації переданого повідомлення. Оцінка має бути оптимальною у тому чи іншому розумінні.

Як і в задачах перевірки гіпотез та оцінювання параметрів, насамперед, необхідно ввести (показники) критерії якості рішення та критерії їх оптимальності.

Якщо розв’язувати задачу фільтрування при кожному фіксованому значенні часу, можна використовувати всі критерії, введені в задачах оцінювання параметрів: середнього ризику, середньоквадратичні похибки, критерій правдоподібності тощо. Проте оцінювання повідомлення виконується на деякому фіксованому інтервалі часу і тому іноді придатними будуть інші критерії, що враховують якість відновлення реалізації у цілому.

Найчастіше використовується критерій середньоквадратичної похибки, що вводиться для кожного  на інтервалі часу:

. (24)

Співвідношення (24) можна подати так:

. (24а)

Відповідний критерій оптимальності рішення задається у вигляді вимоги мінімізації похибки (24а):

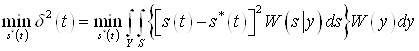, (25)

Мінімум у (24) забезпечується, якщо мінімізувати функціонал

, (26)

тобто якщо забезпечити мінімізацію середньоквадратичної похибки при кожному спостереженні . Результат рішення – оцінка  передавання повідомлення.

Найпростіша задача (24а) приводить до лінійного фільтрування.