Навигация
Расчет фильтра нижних частот
Содержание
Введение
1 Физические основы и принцип действия широкополосных фильтров
2 Пример расчета фильтра нижних частот на заданные параметры
Заключение
Список использованной литературы
Введение
Во многих радиотехнических устройствах часто возникает необходимость выделения заданных частотных диапазонов из имеющегося спектра частот. Выделение требуемой полосы частот с очень малым затуханием осуществляется фильтрами.
В начале нашего столетия электрические фильтры, составленные из ряда катушек индуктивности и конденсаторов, получили широкое применение в технике. Благодаря их применению оказалось возможным осуществление многих магистралей дальней телефонной, телеграфной и других видов связи.
Известный интерес представляют пассивные цепочные, или лестничные фильтры, состоящие из комбинаций элементов L и C и не требующие источника питания. Пассивные фильтры могут обладать как широкими полосами пропускания, так и очень узкими.
При расчете фильтра, с одной стороны, необходимо определить, с какими допустимыми искажениями передается входной сигнал, являющийся функцией частоты или времени, на выход фильтра, и, с другой стороны, из каких конкретных элементов должен состоять этот фильтр. Получение наивыгоднейших выходных характеристик с минимальными искажениями и создание принципиальной схемы фильтра с минимальным числом элементов, осуществляющей требуемую передачу сигнала, является содержанием расчета фильтров.
1 Физические основы и принцип действия широкополосных фильтров
В электрических, радиотехнических и телемеханических установках часто решается задача: из совокупного сигнала, занимающего широкую полосу частот, выделить один или несколько составляющих сигналов с более узкой полосой. Сигналы заданной полосы выделяют при помощи частотных электрических фильтров.
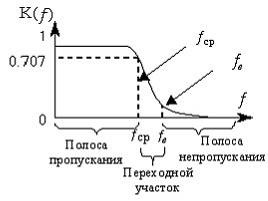
К частотным электрическим фильтрам различной аппаратуры предъявляются разные, порой противоречивые требования. В одной области частот, которая называется полосой пропускания, сигналы не должны ослабляться, а в другой, называемой полосой задерживания, ослабление сигналов не должно быть меньше определенного значения. Фильтр считают идеальным, если в полосе пропускания отсутствует ослабление сигналов и фазо-частотная характеристика линейна (нет искажения формы сигналов), а вне полосы пропускания сигналы на выходе фильтра отсутствуют.
Фильтры могут быть однозвенные (первого порядка), двухзвенные (второго порядка) и многозвенные (n- го). Чем выше порядок фильтра, тем круче его амплитудно-частотная характеристика и тем более она похожа на его идеальную характеристику. Фильтр любого порядка можно построить путем каскадного соединения фильтров первого и второго порядков.
Электрический фильтр представляет собой четырехполюсник, предназначенный для выделения из состава сложного электрического колебания частотных составляющих, расположенных в заданной полосе частот, и подавления тех составляющих, которые расположены в других полосах частот. Первая из названных полос представляет собой полосу пропускания, а вторая – полосу задерживания.
По взаимному расположению полос пропускания и полос задерживания различают фильтры нижних частот, фильтры верхних частот, полосовые и режекторные фильтры.
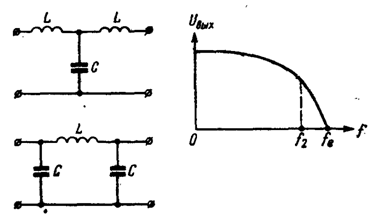
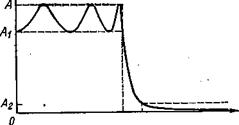
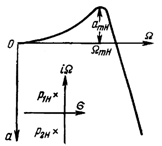
Фильтры нижних частот (ФНЧ) пропускают сигналы частот от 0 до ![]() и задерживающей колебания любых белее высоких частот (рис.1).
и задерживающей колебания любых белее высоких частот (рис.1).
LC–фильтр нижних частот (рис. 6.3,а) пропускает электрические колебания в полосе частот от 0 до
![]() .
.
Это объясняется тем, что на низких частотах сопротивление индуктивного элемента XL фильтра мало, а емкостного XC – велико и электрические колебания проходят со входа на выход почти без ослабления. С увеличением частоты сопротивление индуктивного элемента возрастает, а емкостного – снижается и коэффициент передачи фильтра уменьшается (рисунок 1–б).
Фильтры верхних частот (ФВЧ), напротив, пропускают сигналы, частоты которых простираются от ![]() до
до ![]() , и задерживают сигналы более низких частот(рис.2).
, и задерживают сигналы более низких частот(рис.2).
Полосовые фильтры (ПФ) пропускают сигналы в полосе частот от ![]() до
до ![]() (рис.3).
(рис.3).
Режекторные (заграждающие) фильтры (РФ) задерживают сигналы в полосе частот от ![]() до
до ![]() (рис.4).
(рис.4).
 (а)
(а)
 (б)
(б)
Рисунок - 1 Фильтры нижних частот (а) и его АЧХ (б).

Рисунок - 2 Фильтры верхних частот
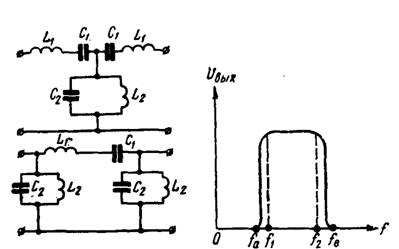
Рисунок – 3 Полосовые фильтры
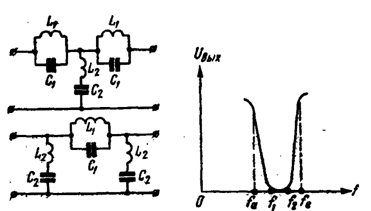
Рисунок – 4 Заграждающие фильтры
Широкополосный фильтр состоит из звеньев, включающих в себя только элементарные контуры. Поэтому механизм фильтрации в широкополосных фильтрах определяется в основном процессами, происходящими в элементарны контурах, т. е. в двухэлементных двухполюсниках, имеющих одну резонансную частоту.
Полное сопротивление Z любого элементарного контура состоит из активной R и реактивной X составляющих:
Z = R + jX (1)
или
Y = G + jB (2)
где Y – полная проводимость
G – активная составляющая полной проводимости
B – реактивная составляющая поной проводимости
Реактивное сопротивление последовательного контура на частоте ![]() =
=![]() равно нулю, активное сопротивление при этом мало, так как оно определяется только потерями в контуре; полное сопротивление контура близко к нулю. Поэтому последовательные контуры применяются в параллельных плечах Т-образных звеньев фильтров верхних частот (рис.5)., так как они оказывают сильное шунтирующее действие на частотах, близких к резонансной.
равно нулю, активное сопротивление при этом мало, так как оно определяется только потерями в контуре; полное сопротивление контура близко к нулю. Поэтому последовательные контуры применяются в параллельных плечах Т-образных звеньев фильтров верхних частот (рис.5)., так как они оказывают сильное шунтирующее действие на частотах, близких к резонансной.
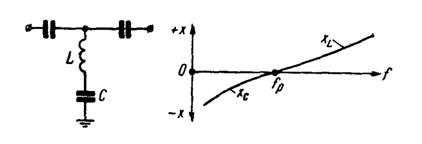
Рисунок – 5 Схема звена ФВЧ и резонансные характеристики последовательного контура
Реактивная проводимость ![]() =
=![]() равна нулю. Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот (рис.6). Резонансные частоты элементарных контуров равны частотам бесконечного затухания соответствующих звеньев
равна нулю. Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот (рис.6). Резонансные частоты элементарных контуров равны частотам бесконечного затухания соответствующих звеньев ![]() =
=![]() . Резонансные частоты контуров, или частоты бесконечного затухания, для ФНЧ располагаются выше частот полосы пропускания (
. Резонансные частоты контуров, или частоты бесконечного затухания, для ФНЧ располагаются выше частот полосы пропускания (![]() >
>![]() ), а для ФВЧ – ниже (
), а для ФВЧ – ниже (![]() <
<![]() ). Параллельные плечи фильтра шунтируют частоты полосы задерживания в то время, как последовательные являются для них пробкой. В полосе пропускания сопротивление параллельных плеч фильтра , напротив, велико, а сопротивление последовательных плеч близко к нулю.
). Параллельные плечи фильтра шунтируют частоты полосы задерживания в то время, как последовательные являются для них пробкой. В полосе пропускания сопротивление параллельных плеч фильтра , напротив, велико, а сопротивление последовательных плеч близко к нулю.
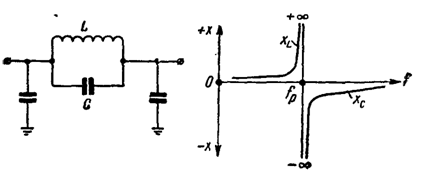
Рисунок – 6 Схема звена ФНЧ и резонансные характеристики параллельного контура
Благодаря этому через фильтр беспрепятственно проходят частоты полосы пропускания. В этой связи становится понятным, почему в широкополосных фильтрах все звенья настраиваются на частоты полосы задерживания.
Крутизна частотной характеристики фильтра в переходной области зависит от числа звеньев. Широкополосный фильтр всегда состоит из фильтра нижних частот и фильтра верхних частот. Полоса пропускания широкополосный фильтра ![]() -
- ![]() образуется благодаря перекрытию полос пропускания ФНЧ (0 -
образуется благодаря перекрытию полос пропускания ФНЧ (0 -![]() ) и ФИЧ (
) и ФИЧ (![]() -
- ![]() ) - (рис.7)
) - (рис.7)
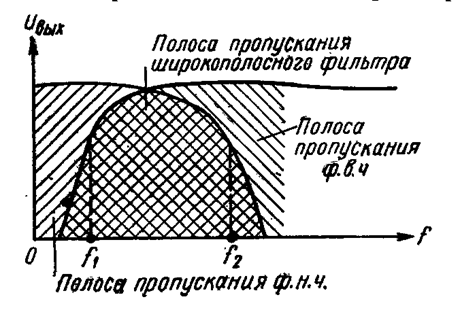
Рисунок – 7 Образование полосы пропускания широкополосного фильтра
Похожие работы
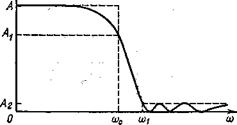
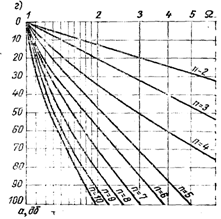
... является эллиптический фильтр, характеристики которого значительно лучше характеристик фильтра Чебышева. Рис. 1.5.3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка Рис. 1.5.4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка 1.6 Фильтры нижних частот на ИНУН Схема на ИНУН, реализующая функцию фильтра нижних частот Баттерворта ...
... целесообразно решать аппроксимационную задачу. Определим нормированную частоту ограничения фильтра, как отношение = = 0,6666. Нормированная частота в полосе задерживания обычного фильтра НЧ равна . Эта же частота в случае фильтра НЧ с ограниченной полосой пропускания рассчитывается по формуле Из кривых (рис. 1.) по вычисленной и заданным и а определим ...
... ; MOV X1, X ; MOV Y1, Y ; RETI ;возврат из подпрограммы обслуживания прерывания по входу END Исходные определения и ручной расчёт результатов работы программы: "Цифровой фильтр (нижних частот)". Разностное уравнение имеет вид: Представим уравнение в виде: , где , 1)Реализуемый коэффициент масштабирования (число без знака) при 8-разрядном формате беззнаковых коэффициентов: ;, ...
... случае a характеризует затухание. Например, предположим, что на рис. 2 выбрано A=1, которому соответствует a=0. Тогда если то затухание на частоте wc a1=-20´lg(1/20,5)=10´lg2=3 дБ. активный полосовой фильтр частотный В основном пропускание в полосе пропускания никогда не превышает 3 дБ. Таким образом, из приведенного примера следует, что значение АЧХ в полосе пропускания ...
0 комментариев