Навигация
3.3 Двоїстий симплекс-метод
Двоїстий симплекс-метод розроблений згодом після прямого симплекс-методу, і який є, по суті, симплекс-методом розв'язання двоїстої задачі лінійного програмування, але сформульованої в термінах вихідної задачі.
Симплекс метод приміняється для рішення задач с невідємними вільними членами ві і вільні у виборі знаку приведеними коефіцієнтами цільової функції сj’. Іноді буває легше знайти базис, який задовільняє ознаку оптимальності (усі сj’ ≥0), але не задовільняє критерії допуску (не всі ві ≥0). Варіант симплекс метода, який приміняється для рішення таких задач, називається двоїстим симплекс методом. За його допомоги рішаються задачі лінійного програмування виду:
 (4.3.1)
(4.3.1)
де система обмежень має такий вигляд і всі приведені коефіцієнти цільової функції сj’ ≥0, і=1,n. При цьому умова ві ≥0, і=1,т , не потрібно. Виділену таким методом задачу будемо називати задачею в двоїстій базисній формі. Вона має базисне, але не опорне рішення.
Двоїстий симплекс метод, який приміняється до задачі в двоїстій базисній формі, приводить до послідовності задач із збільшуючим значаченням цільової функції з невідємними коефіцієнтами сj’ , j=1,n і значеннями ві, і=1,т будь-якого знаку. Двоїстий симплекс метод називають методом поступового покращення оцінок. Перебудова задачі виконується до тих пір, поки не буде встановлено, що вихідна задача не має допустимого рішення або буде отримана задача з допустимим базисним планом (всі ві ≥0), який одночасно буде і оптимальним.
Розглянемо етапи рішення задач ЛП двоїстим симплекс методом:
1. Привести вихідну задачу до канонічного виду.
2. Виключити базисні змінні із цільової функції z.
3. Перевірити приведені коефіцієнти цільової функції: якщо всі преведені коефіцієнти сj’ ≥0, j=1,n, а серед значень ві, і=1,т, є від'ємні, то задача рішається двоїстим симплекс методом. Якщо серед приведених коефіцієнтів сj’ є додатні, то в системі обмежень слід пребудувати вільні члени в невід'ємні (перемноживши на число (-1) стрічки, які містять від'ємні ві) і вирішувати задачу прямим симплекс методом.
4. Опис логічної структури програми
Дана програма умовно розділена 8 модулів, які і утворюють програму, що розв′язує дану нам систему сиплекс методом. Всього є 8 модулів. Кожний модуль окремо відповідає за певну функцію, яку він повинен виконувати.
1. Модулі під назвою „colorPanel” та „numberCrunchingFrame”. Дані модулі відповідають за візуальне оформлення нашої програми. В ньому ми реалізовуєм кольори вікон,клавіші за допомогою яких ми будемо вводити данні і просуватися по програмі, розміри та всі інші параметри, які мають відношення до візульного оформлення нашої програми.
2. ”SimplexTool.java” В даному модулі ми ініціалізуємо основне вікно нашої програми. В ньому ми вводимо всі обмеження: кількість рівнянь в нашій системі (Constraint) та кількість обмежень (Variable).
3. Модуль „Matrix.java” даний модуль проводить всі дії з матрицями. Знаходить визначники, і т.д.
4. „Numbertextfield.java” Даний модуль перевіряє дані, які ввели з клавіатури на правильність. Тобто перевіряє правальність заданої кількості (в дані програмі можливо тільки від 2 до 7) рівнянь та обмежень функції.
5. „problemDimensionWindow.java” Даний модуль відповідає за діалогове вікно в яке ми вводимо початкові дані (коефіцієнти функції, рівнянь нашої системи рівнянь та знаки рівності або нерівності)
6. Модуль „revisedSimplex.java” реалізує сам симплекс метод. Наведемо деякі методи з даного класу:
а) public revisedSimplex(int nv, int nc) – ініціалізує об’єкти класу revisedSimplex: nv (Number of Variables – кількість рівнянь), nc (Number of Constrains – кількість обмежень)
б) public int iterateOneStep() – виконання поточної ітерації
в) public int iterateOneStep()- відповідає за проведення усіх кроків одної ітерації.
г) public float calculateObjective() – функція знаходження значення цільової функції.
д) public void chooseLeavingVariable() – знаходження змінної , яка буде виведена із базису.
е) public void updateSolution() – функція, яка обновляє рішення задачі
є) public void ChooseEnteringVariable() - знаходження змінної , яка буде введена в базис.
ж) public boolean testUnboundedness() – функція перевірки існування рішення.
з) public void calculateReducedCosts() – підрахунок значень індексної стрічки (![]() )
)
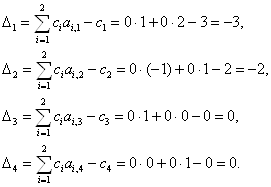 (4.1)
(4.1)
и) public boolean testForOptimality() – перевірка, чи являється поточне значення цільової функції оптимумом, тобто вірним рцшенням.
і) private void makeBt() – заповнення матриці вільних членів
private void makeB() – заповнення основної матриці.
й) public void addConstraint(float [] coefficients, float rhs, int type) – додавання умови
к) public void specifyObjective(float [] coefficients, boolean type) – відповідає за ініціалізацію цільової функції
л) public boolean preprocess(int numberOfVariables, int numberOfConstraints) – функція, заповнення и виведення данних, які ми вводимо на екран.
м) public void SetCostForPhaseOne() - визначає можливість вирішення данної задачі.
н) public float Dot (float []row, float []col, int size) - підраховування суми:
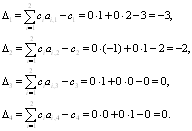 (4.2)
(4.2)
о) public void reset(int numberOfVariables, int numberOfConstraints) – функція, яка закриває поточне вирішення задачі і дає можливість вести нові початкові дані.
7. Модуль „enterDataFrame.java” Модуль за допомогою якого дані, які вводить користувач присвоюються виділеним змінним. Тобото проводить їх ініціалізацію.
5. Технічні засоби
У розробленні даної програми було використано обладнання з такими характеристиками: а) Процесор: Intel Pentium 4, 1,8 Ггц; б) ОЗУ: 256 Мб; в) HDD: 40 Гб; г) Відеокарта – GeForce 5500 – 128 Mб; д) операційна система Windows XP Professional SP2;
Вище приведені дані саме того комп′ютера, на якому розроблялась програма. Ця програма не тестувалась на іншому обладнанні, але за її складністю та використанню ресурсів (приблизно 19 000 Кб) можна сказати, що дана програма не потребує великого об′єму пам′яті, що дасть їй можливість коректно працювати і на іншому обладнанні нижчого рівня, ніж приведений.
6. Виклик та завантаження програми
Для того, щоб скористуватися даною програмою потрібно просто скопіювати її на жорсткий диск. Детальнішої установки вона не потребує. Для запуску програми потрібно вибрати файл з назвою “run (пакетний файл MS-DOS)” та запустити його на виконання. Після проведення даної дії з′явиться діалогове вікно роботи з програмою.
7. Вхідні та вихідні данні
Після запуску програми на виконання програма пропонує ввести такі данні: а) кількість рівнянь та кількість обмежень; б) після цього з’являється вікно в якому потрібно ввести коефіцієнти функції та коефіцієнти рівнянь системи; в) потім потрібно вибрати куди прямує функція (МАХ або MIN); г) вибрати знаки рівності або нерівності (=, ≥, ≤)
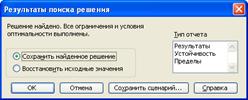
Після того, як програма все підрахує на екрані з’являється матриця, в якій будуть знаходитись відповідь та повідомлення рішення даної задачі або неможливість рішення.
8. Інструкція для користувача
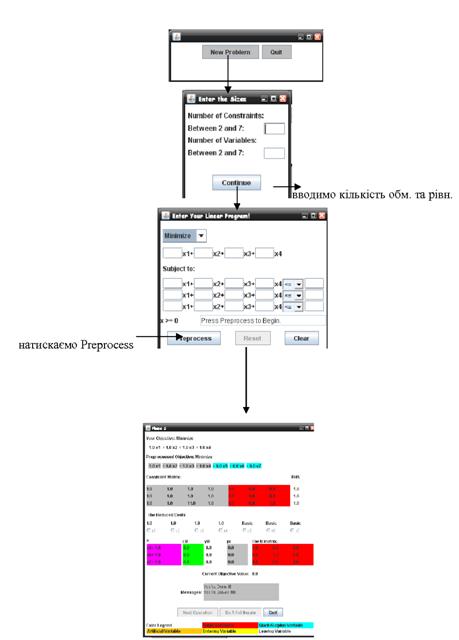
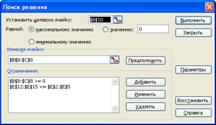
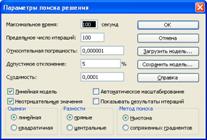
Для коректної роботи з програмою потрібно мати певну базу знань англійської мови, адже всі посилання, назви, та написи на клавішах написано виключно на англійські мові. Щодо користування даної програми, то воно досить просте та елементарне: вводите в діалоговому вікні коефіцієнти функції та систем рівнянь, вибираєте МАХ або MIN (відповідно до задачі, яка перед вами ставиться) та натискаєте клавішу рішення. Далі є два варіанти подальшої роботи з програмою – перший – це одразу отримати кінцевий результат, а інший – натискати клавішу виконання завдання декілька раз. Другий спосіб дає можливість поступово (крок за кроком) спостерігати за роботою програми та вирішенні задачі. Все це представлено на рис. 9.1
Висновки
В даній роботі ми розглянули одну з задач лінійного програмування та методи її вирішення. Один з методів покладений в основу роботи даної програми – симплекс метод. Виконуючи курсову я вдосконалив свої знання та навички використання мови програмування Java. Робота вимагала знань основ алгоритмічної мови, вміння складати програми різної складності використовуючи дану мову програмування. Я вдосконалив свої знання у області роботи з класами, методами, функціями та вказівниками. Набув суттєвих практичних навиків у роботі з компілюванням файлів Java.
Література
1 Симплекс метод. Материал из Википедии — свободной энциклопедии - http://ru.wikipedia.org/wiki/Симплекс метод
2 Еремин И.И., Астафьев Н.Н. Введение в теорию линейного и выпуклого программирования М.: Наука, 1976р. – 409с.
3 Карманов В.Г. Математическое программирование. – М.: Наука, 1986р. -250с.
4 Иванов Ю.П., Лотов А.В. Математические модели в экономике. – М.: Наука, 1979р. -359с.
5 Моисеев Н.Н., Иванов Ю.П., Столярова Е.М. Методы оптимизации. – М.:
Наука, 1978р. -506с.
6 Бронштейн И.Н., Семендяев К.А. Справочник по математике. – М.: Наука, 1986р.560с.
7 Коробов П.Н. Математическое программирование и моделирование
экономических процессов.- С.Т.Б. Издательство ДНК 2003р. -601с.
Похожие работы
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
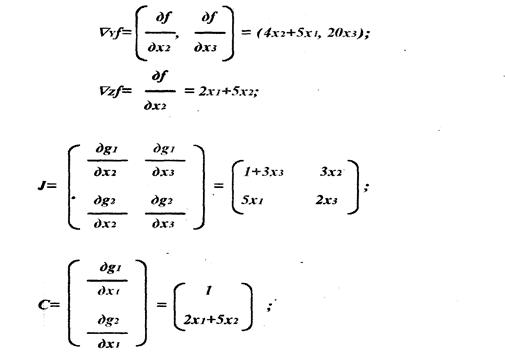
... і екстремуми, полягає в послідовному виборі числових значень , після реалізації, якого дана система зважується відносно х. 3. ВИКОРИСТАННЯ МЕТОДУ ЯКОБІ ДЛЯ РІШЕННЯ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ Дано задачу лінійного програмування, у якій потрібно максимізувати z=2xi+3xa при обмеженнях х1+х2+х3=5 х1-х2+х4=3 х1,х2,х3,х4>0 Розглянемо обмеження xj>0 устанавлюючи не заперечність перемі ...
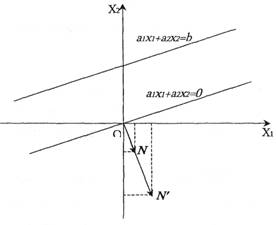
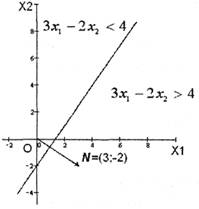
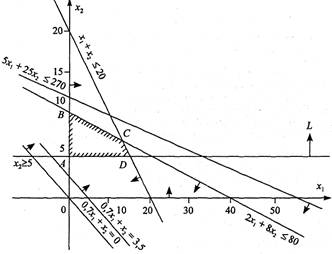
... зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення. Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних, Розглянемо розв' ...
... , а при більшому числі змінних - взагалі неможливим. Незважаючи на це, розгляд графічного методу дасть змогу зробити висновки, що послужать основою для розробки загального методу розв’язання задач лінійного програмування[2]. Перший крок при використанні графічного методу полягає в поданні області допустимих розв’язків, у якій водночас задовольняються всі обмеження моделі. Нехай шукана область ( ...
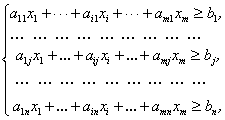
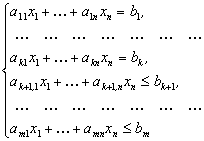
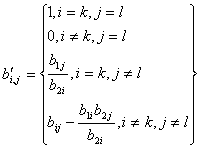
0 комментариев