Навигация
Основные принципы обнаружения и исправления ошибок
10.1 Основные принципы обнаружения и исправления ошибок
Рассмотрим два основных метода использования избыточности для защиты от ошибок. В первом методе, обнаружение ошибок и повторная передача, для проверки на наличие ошибки используется контрольный бит четности (дополнительный бит, присоединяемый к данным). При этом приемное оконечное устройство не предпринимает попыток исправить ошибку, оно просто посылает передатчику запрос на повторную передачу данных. Следует заметить, что для такого диалога между передатчиком и приемником необходима двухсторонняя связь. Второй метод, прямое исправление, требует лишь односторонней линии связи, поскольку в этом случае контрольный бит четности служит как для обнаружения, так и исправления ошибок. Далее мы увидим, что не все комбинации ошибок можно исправить, так что коды коррекции классифицируются в соответствии с их возможностями исправления ошибок.
Принцип обнаружения и исправления ошибок кодами хорошо иллюстрируется с помощью геометрических моделей. Любой n- элементный двоичный код можно представить n – мерным кубом, в котором каждая вершина отображает кодовую комбинацию, а длина ребра куба соответствует одной единице. В таком кубе расстояние между вершинами измеряется минимальным количеством ребер, находящихся между ними, обозначается d и называется кодовым расстоянием.
10.2 Кодовое расстояние и корректирующая способность кода
Кодовое расстояние – это минимальное число элементов, в которых любая кодовая комбинация отличается от другой ( по всем парам кодовых слов). Например, код состоит из комбинаций 1011, 1101, 1000, и 1100. Сравнивая первые две комбинации, путем сложения их по модулю 2 находим, что d=2. Наибольшее значение d=3 получается при сравнении первой и четвертой комбинации, а наименьшее d=1 – второй и четвертой, третьей и четвертой комбинации. Выберем в трехмерном кубе такие вершины, кодовые обозначения которых отличались бы друг от друга на d=3. Такие вершины расположены на концах пространственных диагоналей куба. Их может быть только четыре пары: 000 и 111, 001 и 110, 100 и 011, 010 и 101. Код, образованный по такому правилу, может исправить одиночную ошибку или обнаружить две одиночные ошибки.
Корректирующая способность кода зависит от кодового расстояния: а) при d=1 ошибка не обнаруживается; б) при d=2 обнаруживаются одиночные ошибки; в) при d=3 исправляются одиночные ошибки или обнаруживаются двойные ошибки. В общем случае
![]() (10.1)
(10.1)
где d- минимальное кодовое расстояние, r- число обнаруживаемых ошибок, s- число исправляемых ошибок. При этом обязательным условием является r≥s.
10.3 Классификация корректирующих кодов
Корректирующими называются коды, позволяющие обнаружить и исправить ошибки в кодовых комбинациях. Они делятся на две группы: 1) коды с обнаружением ошибок; 2) коды с обнаружением и исправлением ошибок.
1) Особенность кодов с обнаружением ошибок состоит в том, что кодовые комбинации, входящие в их состав, отличаются друг от друга не менее, чем на d=2. Их можно условно разделить на две группы:
а) коды, построенные путем уменьшения числа используемых комбинаций.
Код с постоянным числом единиц и нулей в комбинациях (код с постоянным весом).
![]() (10.2)
(10.2)
где l – число единиц в слове длиной n.
Распределительный код ![]() Это также разновидность кода с постоянным весом, равным единице. В любой кодовой комбинации содержится только одна единица. Число кодовых комбинаций в распределительном коде
Это также разновидность кода с постоянным весом, равным единице. В любой кодовой комбинации содержится только одна единица. Число кодовых комбинаций в распределительном коде
![]() (10.3)
(10.3)
Кодовые комбинации при n=6 можно записать в виде 000001,000010,000100,001000,010000,100000. Сложение по модулю 2 двух комбинаций показывает, что они отличаются друг от друга на кодовое расстояние d=2.
Т а б л и ц а 10.1 - Код с постоянным числом единиц и нулей
| Код | Код |
| 11000 10010 01010 00011 01100 01001 00101 10001 00110 10100 | 1010100 0101010 1110000 0000111 1001001 |
б) коды, в которых используются все комбинации но к каждой из них по определенному правилу добавляются контрольные символы m - символы.
Код с проверкой на четность. Такой код образуется путем добавления к передаваемой комбинации, состоящей из к информационных символов неизбыточного кода, одного контрольного символов m (0 или 1), так, чтобы общее число единиц в передаваемой комбинации было четным. В общем случае
![]() (10.4)
(10.4)
Т а б л и ц а 10.2 - Код с проверкой на четность
| Информационные символы к | Контрольные символы m | Полная кодовая комбинация n=k+m |
| 1 | 2 | 3 |
| 11011 10101 00010 11000 11110 11111 | 0 1 1 0 0 1 | 110110 101011 000101 110000 111100 111111 |
Общее число комбинаций N=2n-1
Код с числом единиц, кратным трем. Этот код образуется добавлением к к информационным символам двух дополнительных контрольных символов (m=2), имеющих такие значения, чтобы сумма единиц, посылаемых в линию кодовых комбинаций, была кратной трем
Т а б л и ц а 10.3
| Информационные символы к | Контрольные символы m | Полная кодовая комбинация |
| 000110 100011 101011 | 10 00 11 | 00011010 10001100 10101111 |
2) Особенность кодов с обнаружением ошибок в том, что они образуют корректирующий код, который позволяет не только обнаруживать, но и исправлять ошибки. Составление корректирующих кодов производят по следующему правилу: сначала определяют количество контрольных символов, которое следует добавить к данной кодовой комбинации, состоящей из информационных символов. Далее устанавливают место, где эти контрольные символы должны быть расположены и их состав. На приеме обычно делают проверку на четность определенной части разрядов.
Коды Хемминга. Коды Хэмминга (Hamming codes) — это простой класс блочных кодов, которые имеют следующую структуру:
![]() (10.4)
(10.4)
где m= 2,3,..Минимальное расстояние этих кодов равно 3, поэтому они способны исправлять вес однобитовые ошибки или определять все ошибочные комбинации из двух или менее ошибок в блоке. Декодирование с помощью синдромов особенно хорошо подходит к кодам Хэмминга. Фактически синдром можно превратить в двоичный указатель местоположения ошибки. Хотя коды Хэмминга не являются слишком мощными, они принадлежат к очень ограниченному классу блочных кодов, называемых совершенными.
Циклические коды. Важным подклассом линейных блочных кодов являются двоичные циклические коды (cyclic codes). Код легко реализуется на регистре сдвига с обратной связью; на подобных регистрах сдвига с обратной связью вычисляется синдром; алгебраическая структура циклического кода естественным образом позволяет эффективно реализовать методы декодирования. Итак, линейный код (n, к) называется циклическим, если он обладает следующим свойством. Если n-кортеж U= (u0, u1, и2, …, un-1) является кодовым словом в подпространстве S, тогда U(1)= (un-1, u0, u1, и2,..., un-1), полученный из U с помощью циклического сдвига, также является кодовым словом в S. Или, вообще, U(i) = (un-i;. un-i+1,…, un-1, u0, u1,… un-i-1), полученный i циклическими сдвигами, является кодовым словом в S.
Циклический код Файра. Циклические коды, обнаруживающие и исправляющие пакеты ошибок (коды Файра). Под пакетом ошибок длиной b понимают такой вид комбинации помехи, в которой между крайними разрядами, пораженными помехами, содержится b-2 разряда. Например, при b=5 комбинации помехи, т.е. пакет ошибок, могут иметь следующий вид: 10001 (поражены тоько два крайних символа), 11111 (поражены все символы), 10111, 11101, 11011 (не поражен лишь один символ), 10011, 11001, 10101 (поражены три символа). При любом варианте непременным условием пакета данной длины является поражение крайних символов.
Коды Файра могут исправлять пакет ошибок длиной b и обнаруживать пакет ошибок длиной b [заметим, что в кодах Файра понятие кодового расстояния - d].
Коды Боуза-Чоудхури-Хоквингэма.![]() . Эти коды, разработанные Боузом, Чодхури и Хоквинхемом (сокращенно коды БЧХ), позволяют обнаруживать и исправлять любое число ошибок. Заданными при кодировании является число ошибок s, которое следует исправить, и общее число символов, посылаемых в линию, т.е. длина слов n. Числа информационных символов k и контрольных символов m, а также состав контрольных символов подлежат определению.
. Эти коды, разработанные Боузом, Чодхури и Хоквинхемом (сокращенно коды БЧХ), позволяют обнаруживать и исправлять любое число ошибок. Заданными при кодировании является число ошибок s, которое следует исправить, и общее число символов, посылаемых в линию, т.е. длина слов n. Числа информационных символов k и контрольных символов m, а также состав контрольных символов подлежат определению.
Коды БЧХ для обнаружения ошибок. Их строят следующим образом. Если необходимо образовать код с обнаружением четного числа ошибок, то по заданному числу r находят значения d и s. Дальнейшее кодирование выполняют, как и ранее. Если требуются обнаружить нечетное число ошибок, то находят ближайшее меньшее целое число s и кодирование производят так же, как и в предыдущем случае: образующий многочлен дополнительно умножают на двучлен ![]() . Например, требуются построить код обнаруживающий семь ошибок при n=15. Находим, что d=8, а ближайшее меньшее значение s=3. Далее определяем многочлен
. Например, требуются построить код обнаруживающий семь ошибок при n=15. Находим, что d=8, а ближайшее меньшее значение s=3. Далее определяем многочлен ![]() , как указано в примере 3.5, и умножаем его на двучлен
, как указано в примере 3.5, и умножаем его на двучлен ![]() , т.е. получаем
, т.е. получаем ![]() . Таким образом построен код БЧХ(15,4).
. Таким образом построен код БЧХ(15,4).
Похожие работы
... и задачи их функционирования. Курсовой проект по данной дисциплине позволяет более подробно изучить разделы данной дисциплины. Целью данной курсовой работы является освоение курса «Технологии цифровой связи» и получение навыков в решении задач. В курсовой работе необходимо спроектировать тракт передачи данных между источником и получателем информации. Так как необходима высокая верность передачи ...
... телекоммуникаций играет важную роль - настройка и оптимизация сетей связи, поиск неисправностей и причин конфликтов, разрешение конфликтных ситуаций. Таким образом, основной движущей силой развития измерительных технологий является усложнение современных систем связи. Распространенное мнение о том, что цифровые системы связи лучше, надежнее и поэтому требуют в меньшей степени обслуживания на ...
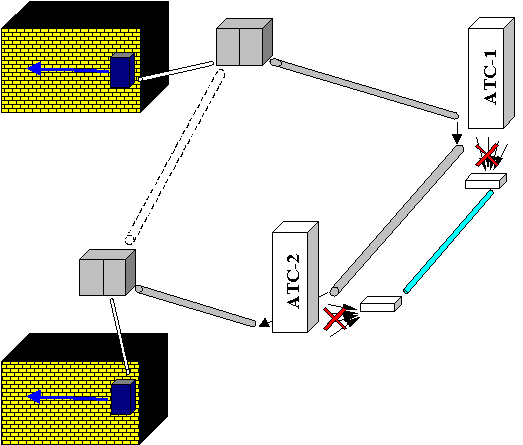
... после сбоев, резервное копирование пользовательских настроек и безопасность всей системы. Технология DSL: Краткий глоссарий ADSL Asymmetric Digital Subscriber Line - асимметричная цифровая абонентская линия, асимметричная DSL. Технология, обеспечивающая речевую связь и высокоскоростную передачу данных по обычным телефонным линиям. Скорость передачи от АТС к абоненту значительно выше, чем ...
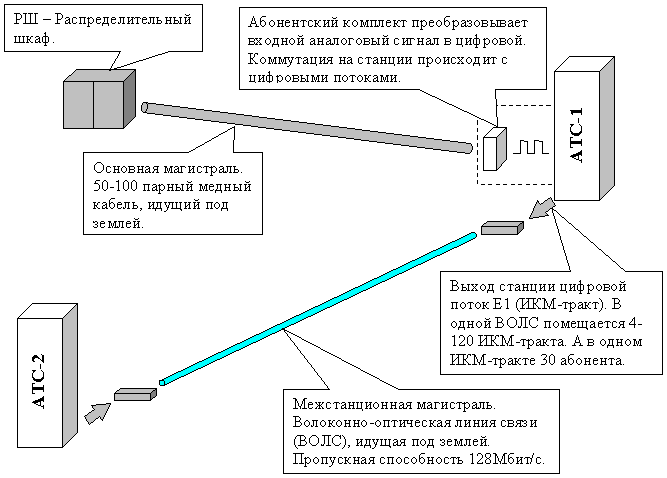
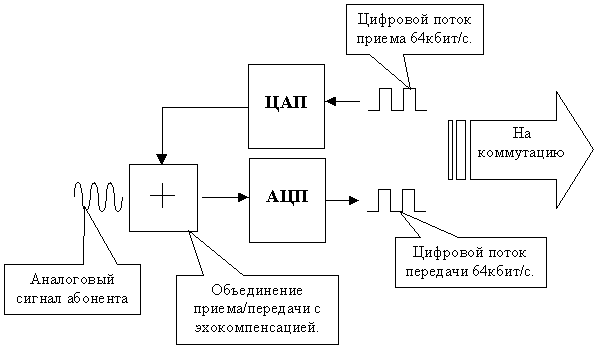
... , а манипуляция цифровым потоком во внутриканальном пространстве и распределение этого потока в выделенные интервалы передачи. За счет этого электронные АТС имеют идеальное качество “контакта” и благодаря использованию цифровых технологий “шум станции” на линию не проходит. Однако есть и обратная сторона медали: “шум квантования”. Шум вызван квантованием аналоговых сигналов, необходимый для ...
0 комментариев