Лекция №1. Элементы систем цифровой связи
Лекция №2. Каналы связи и их характеристики
Лекция №3. Математические модели каналов связи
Лекция №4. Узкополосная передача
Обнаружение сигнала в гауссовом шуме
Биполярный метод
Лекция №6. Полосовая модуляция и демодуляция
Амплитудная манипуляция
Векторное представление сигналов MFSK (многочаcтотная фазовая манипуляция)
Лекция №8. Спектральные характеристики модулированных колебаний
Цифровой согласованный фильтр
Синхронизация поэлементная, групповая и цикловая
Основные принципы обнаружения и исправления ошибок
Лекция №11. Помехоустойчивые коды и методы декодирования корректирующих кодов
Лекция №12. Системы связи с обратной связью
Структурная схема системы с информационной обратной связью (ИОС) и решающей обратной связью (РОС), характеристики и алгоритмы работы
Лекция №13. Сжатие данных в ЦСС
Навигация
Векторное представление сигналов MFSK (многочаcтотная фазовая манипуляция)
Технология цифровой связи
119269
знаков
7
таблиц
35
изображений
7.2.1 Векторное представление сигналов MFSK (многочаcтотная фазовая манипуляция)
Поскольку сигнальное пространство MFSK описывается М взаимно перпендикулярными осями, мы без труда можем проиллюстрировать случаи М=2 и М = 3. Итак, на рисунке 7.3, а видим бинарные ортогональные векторы s1 и s2.
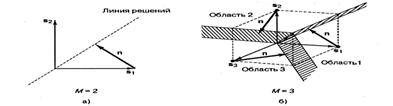
Рисунок 7.3 - Наборы сигналов для MFSK для М=2,3
На рисунке 7.3, б - показано трехмерное сигнальное пространство со взаимно перпендикулярными координатными осями. В этом случае плоскости решений разбивают пространство на три области. Показано, как к каждому сигнальному вектору s1, s2 и s3 прибавляется вектор шума n, представляющий минимальный вектор, который может привести к принятию неправильного решения. Векторы шума на рисунке 7.3, б имеют тот же модуль, что и вектор шума, показанный на рисунке 7.3, a. При данном уровне принятой энергии расстояние между любыми двумя векторами сигналов-прототипов si и sj-М-мерного ортогонального пространства является константой. Отсюда следует, что минимальное расстояние между вектором сигнала-прототипа и любой границей решений не меняется с изменением М. В отличие от модуляции MPSK, когда добавление нового сигнала к сигнальному множеству делало сигналы более уязвимыми к меньшим векторам шума, при MFSK такого не происходит.
Для иллюстрации этого момента можно было бы нарисовать ортогональные пространства высших размерностей, но, к сожалению, это затруднительно. Мы можем использовать только наш «мысленный взгляд», чтобы понять, что увеличение сигнального множества М путем введения дополнительных осей, причем, каждая новая ось перпендикулярна всем существующим, не приводит к его уплотнению. Следовательно, переданный сигнал, принадлежащий ортогональному набору, не становится более уязвимым к шуму при увеличении размерности.
Пониманию улучшения надежности при ортогональной передаче сигналов способствует сравнение зависимости вероятности символьной ошибки (РЕ) от ненормированного отношения сигнал/шум (signal-to-noise ratio — SNR) с зависимостью РЕ от Eb/N0. Стоит отметить, что изучение зависимости достоверности передачи от M при фиксированном SNR не является лучшим направлением в цифровой связи. Фиксированное SNR означает фиксированный объем энергии на символ; следовательно, при увеличении М этот объем энергии необходимо распределять уже между большим числом битов, т.е. на каждый бит приходится меньше энергии. В этой связи наиболее удобным способом сравнения различных цифровых систем является использование в качестве критерия отношения сигнал/шум, нормированного на бит, или Eb/N0. Повышение достоверности передачи с увеличением М проявляется только в том случае, если вероятность ошибки изображается как зависимость от Eb/N0. В этом случае при увеличении М отношение Eb/N0, требуемое для получения заданной вероятности ошибки, снижается при фиксированном SNR; следовательно, нам нужен новый график, где ось абсцисс представляет не SNR, a Eb/N0.
7.2.2 Векторное представление сигналов MPSK (многофазовая манипуляция). На рисунке 7.4 показаны наборы сигналов MPSK для М = 2, 4, 8 и 16. На рисунке 7.4, а видим бинарные (к=1, М = 2) антигодные векторы S1 и s2, угол между которыми равен 180°. Граница областей решений разделяет сигнальное пространство на две области. На рисунке также показан вектор шума n, равный по амплитуде сигналу S1,. При указанных направлении и амплитуде энергия вектора шума является минимальной, и детектор может допустить символьную ошибку.
На рисунке 7.4, б видим 4-арные (k = 2, М = 4) векторы, расположенные друг к другу под углом 90°. Границы областей решений (на рисунке изображена только одна) делят сигнальное пространство на четыре области.
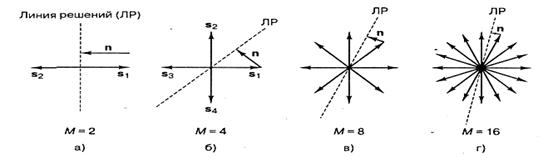
Рисунок 7.4 - Наборы сигналов MPSK для М=2,4,8,16
Здесь также изображен вектор шума n (начало — в вершине вектора сигнала, направление перпендикулярно ближайшей границе областей решений), являющийся вектором минимальной энергии, достаточной, чтобы детектор допустил символьную ошибку. Отметим, что вектор шума минимальной энергии на рисунке 7.4, б меньше вектора шума на рисунке 7.4 а, что свидетельствует о большей уязвимости 4-арной системы к шуму по сравнению с бинарной (энергии сигналов в обоих случаях взяты равными). Изучая рисунок 7.4, в, г, можно отмстить следующую закономерность. При многофазной передаче сигналов по мере роста величины М на сигнальную плоскость помещается все больше сигнальных векторов. По мере того как векторы располагаются плотнее, для появления ошибки вследствие шума требуется все меньше энергии.
С помощью рисунка 7.4 можно лучше понять поведение зависимости вероятности РBот Eb/N0, при росте к. Кроме того, рисунок позволяет взглянуть на природу компромиссов при многофазной передаче сигналов. Размещение большего числа векторов сигналов в сигнальном пространстве эквивалентно повышению скорости передачи данных без увеличения системной ширины полосы (все векторы ограничиваются одной и той же плоскостью). Другими словами, мы повысили использование полосы за счет вероятности ошибки. Рассмотрим рисунок 7.4, г, где из приведенных вариантов вероятность ошибки является наивысшей. Чем мы может заплатить, чтобы "выкупить" возросшую вероятность ошибки? Иными словами, чем мы можем поступиться, чтобы расстояние между соседними векторами сигналов на рисунке 7.4, д стало таким же, как на рисунке 7.4, а, Отметим, что на схемах, изображенных на рисунке 7.4, а для различных значений М, все векторы имеют одинаковую амплитуду. Это равносильно утверждению, что сопоставление различных схем выполняется при фиксированном отношении Es/N0, где Es - энергия символа.
Похожие работы
... и задачи их функционирования. Курсовой проект по данной дисциплине позволяет более подробно изучить разделы данной дисциплины. Целью данной курсовой работы является освоение курса «Технологии цифровой связи» и получение навыков в решении задач. В курсовой работе необходимо спроектировать тракт передачи данных между источником и получателем информации. Так как необходима высокая верность передачи ...
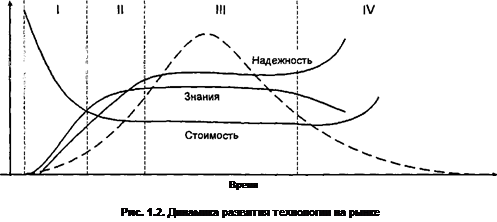
... телекоммуникаций играет важную роль - настройка и оптимизация сетей связи, поиск неисправностей и причин конфликтов, разрешение конфликтных ситуаций. Таким образом, основной движущей силой развития измерительных технологий является усложнение современных систем связи. Распространенное мнение о том, что цифровые системы связи лучше, надежнее и поэтому требуют в меньшей степени обслуживания на ...
... после сбоев, резервное копирование пользовательских настроек и безопасность всей системы. Технология DSL: Краткий глоссарий ADSL Asymmetric Digital Subscriber Line - асимметричная цифровая абонентская линия, асимметричная DSL. Технология, обеспечивающая речевую связь и высокоскоростную передачу данных по обычным телефонным линиям. Скорость передачи от АТС к абоненту значительно выше, чем ...
... , а манипуляция цифровым потоком во внутриканальном пространстве и распределение этого потока в выделенные интервалы передачи. За счет этого электронные АТС имеют идеальное качество “контакта” и благодаря использованию цифровых технологий “шум станции” на линию не проходит. Однако есть и обратная сторона медали: “шум квантования”. Шум вызван квантованием аналоговых сигналов, необходимый для ...
0 комментариев