Непрерывность функции на интервале и на отрезке

10670

знаков

таблиц

изображений

Непрерывность функции на интервале и на отрезке

Определение 3.3 Пусть - некоторая функция, $\mathcal{D}(f)$ - её область определения и $(a;b)\sbs\mathcal{D}(f)$ - некоторый (открытый) интервал (может быть, с $a=-\infty$ и/или $b=+\infty$ )⁷. Назовём функцию непрерывной на интервале если непрерывна в любой точке $x_0\in(a;b)$ , то есть для любого $x_0\in(a;b)$ существует $\lim\limits_{x\to x_0}f(x)=f(x_0)$ (в сокращённой записи: $\forall\ x_0\in(a;b)\ \exists\ \lim\limits_{x\to x_0}f(x)=f(x_0)).$

Пусть теперь - (замкнутый) отрезок в $\mathcal{D}(f)$ . Назовём функцию непрерывной на отрезке , если непрерывна на интервале , непрерывна справа в точке и непрерывна слева в точке , то есть
$1)\quad\forall\ x_0\in(a;b)\ \exists\ \lim\limits_{x\to x_0}f(x)=f(x_0);$

$2)\quad\exists\ \lim\limits_{x\to a+}f(x)=f(a);$ $3)\quad\exists\ \lim\limits_{x\to b-}f(x)=f(b).$

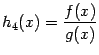Теорема 3.5 Пусть и - функции и - интервал или отрезок, лежащий в $\mathcal{D}(f)\cap\mathcal{D}(g)$ . Пусть и непрерывны на . Тогда функции , , непpеpывны на . Если вдобавок $g(x)\ne0$ пpи всех $x\in I$ , то функция $h_4(x)=\dfrac{f(x)}{g(x)}$ также непpеpывна на .

Из этой теоpемы вытекает следующее утвеpждение, точно так же, как из теоpемы 3.1 - пpедложение 3.3:

Предложение 3.4 Множество $\mathcal{C}_I$ всех функций, непpеpывных на интеpвале или отpезке $I\sbs\mathbb{R}$ - это линейное пpостpанство:

$\displaystyle f_1(x),f_2(x)\in\mathcal{C}_I;C_1,C_2=\mathrm{const}\quad\Longrightarrow \quadC_1f_1(x)+C_2f_2(x)\in\mathcal{C}_I.$

Более сложное свойство непрерывной функции выражает следующая теорема.

Теорема 3.6 (о корне непрерывной функции) Пусть функция непрерывна на отрезке , причём и - числа разных знаков. (Будем для определённости считать, что , а .) Тогда существует хотя бы одно такое значение $x_0\in(a;b)$ , что (то есть существует хотя бы один корень уравнения ).

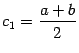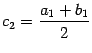Доказательство. Рассмотрим середину отрезка $c_1=\dfrac{a+b}{2}$ . Тогда либо ${f(c_1)=0}$ , либо , либо . В первом случае корень найден: это . В остальных двух случаях рассмотрим ту часть отрезка, на концах которой функция принимает значения разных знаков: в случае или в случае . Выбранную половину отрезка обозначим через и применим к ней ту же процедуру: разделим на две половины и , где $c_2=\dfrac{a_1+b_1}{2}$ , и найдём . В случае корень найден; в случае рассматриваем далее отрезок в случае - отрезок и т.д.

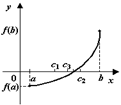
Рис.3.16. Последовательные деления отрезка пополам

Получаем, что либо на некотором шаге будет найден корень , либо будет построена система вложенных отрезков

$\displaystyle [a;b]\sps[a_1;b_1]\sps[a_2;b_2]\sps\ldots\sps[a_i;b_i]\sps\ldots,$

в которой каждый следующий отрезок вдвое короче предыдущего. Последовательность $a_0=a,a_1,a_2,\dots,a_i,\dots$ - неубывающая и ограниченная сверху (например, числом ); следовательно (по теореме 2.13), она имеет предел $\lim\limits_{i\to\infty}a_i=a'$ . Последовательность ${b_0=b,b_1,b_2,\dots,b_i,\dots}$ - невозрастающая и ограниченная снизу (например, числом); значит, существует предел $\lim\limits_{i\to\infty}b_i=b'$ . Поскольку длины отрезков образуют убывающую геометрическую прогрессию (со знаменателем $\frac{1}{2}$ ), то они стремятся к 0, и $\lim\limits_{i\to\infty}a_i=\lim\limits_{i\to\infty}b_i$ , то есть . Положим, теперь . Тогда

$\displaystyle \lim_{i\to\infty}f(a_i)=f(a')=f(x_0)$ и $\displaystyle \lim_{i\to\infty}f(b_i)=f(b')=f(x_0),$

поскольку функция непрерывна. Однако, по построению последовательностей $\{a_i\}$ и $\{b_i\}$ , и , так что, по теореме о переходе к пределу в неравенстве (теорема 2.7), $\lim\limits_{i\to\infty}f(a_i)\leqslant 0$ и $\lim\limits_{i\to\infty}f(b_i)\geqslant 0$ , то есть $f(x_0)\leqslant 0$ и $f(x_0)\geqslant 0$ . Значит, , и - корень уравнения .

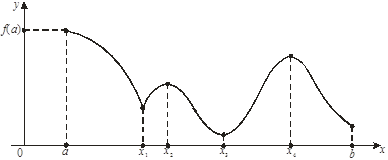
Пример 3.14 Рассмотрим функцию $f(x)=\cos x-x$ на отрезке $[0;\frac{\pi}{2}]$ . Поскольку и $f(\frac{\pi}{2})=-\frac{\pi}{2}$ - числа разных знаков, то функция обращается в 0 в некоторой точке интервала $(0;\frac{\pi}{2})$ . Это означает, что уравнение $\cos x=x$ имеет корень $x_0\in(0;\frac{\pi}{2})$ .

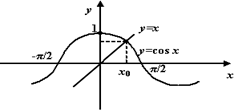
Рис.3.17. Графическое представление корня уравнения $\cos x=x$

Доказанная теорема фактически даёт нам способ нахождения корня , хотя бы приближённого, с любой заданной наперёд степенью точности. Это- метод деления отрезка пополам, описанный при доказательстве теоремы. Более подробно с этим и другими, более эффективными, способами приближённого нахождения корня мы познакомимся ниже, после того, как изучим понятие и свойства производной.

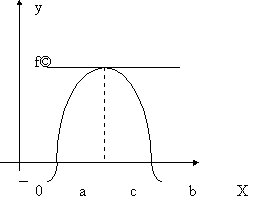
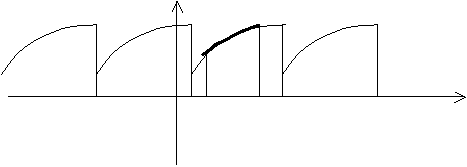
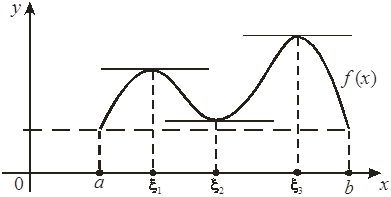
Заметим, что теорема не утверждает, что если её условия выполнены, то корень - единственный. Как показывает следующий рисунок, корней может быть и больше одного (на рисунке их 3).

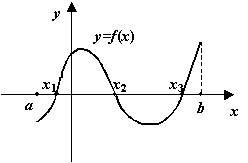
Рис.3.18. Несколько корней функции, принимающей значения разных знаков в концах отрезка

Однако, если функция монотонно возрастает или монотонно убывает на отрезке, в концах которого принимает значения разных знаков, то корень- единственный, так как строго монотонная функция каждое своё значение принимает ровно в одной точке, в том числе и значение 0.

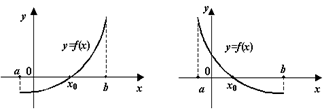
Рис.3.19.Монотонная функция не может иметь более одного корня

Непосредственным следствием теоремы о корне непрерывной функции является следующая теорема, которая и сама по себе имеет очень важное значение в математическом анализе.

Теорема 3.7 (о промежуточном значении непрерывной функции) Пусть функция непрерывна на отрезке и $f(a)\ne f(b)$ (будем для определённости считать, что ). Пусть - некоторое число, лежащее между и . Тогда существует такая точка $x_0\in(a;b)$ , что .

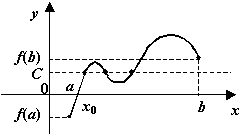
Рис.3.20.Непрерывная функция принимает любое промежуточное значение

Доказательство. Рассмотрим вспомогательную функцию , где $C\in(f(a);f(b))$ . Тогда и . Функция , очевидно, непрерывна, и по предыдущей теореме существует такая точка $x_0\in(a;b)$ , что . Но это равенство означает, что .

Заметим, что если функция не является непрерывной, то она может принимать не все промежуточные значения. Например, функция Хевисайда (см. пример 3.13) принимает значения , , но нигде, в том числе и на интервале , не принимает, скажем, промежуточного значения $\frac{1}{2}$ . Дело в том, что функция Хевисайда имеет разрыв в точке , лежащей как раз в интервале .

Для дальнейшего изучения свойств функций, непрерывных на отрезке, нам понадобится следующее тонкое свойство системы вещественных чисел (мы уже упоминали его в главе 2 в связи с теоремой о пределе монотонно возрастающей ограниченной функции): для любого ограниченного снизу множества $M\sbs\mathbb{R}$ (то есть такого, что $x\geqslant K$ при всех $x\in M$ и некотором ; число называется нижней гранью множества ) имеется точная нижняя грань $\inf M$ , то есть наибольшее из чисел , таких что $x\leqslant K$ при всех $x\in M$ Аналогично, если множество ограничено сверху, то оно имеет точную верхнюю грань $\sup M$ : это наименьшая из верхних граней (для которых $x\leqslant K$ при всех $x\in M$ ).

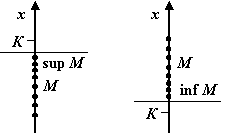
Рис.3.21.Нижняя и верхняя грани ограниченного множества

Если $x_0=\inf M$ , то существует невозрастающая последовательность точек ${x_1\geqslant x_2\geqslant \dots\geqslant x_i\geqslant \dots}$ , которая стремится к . Точно так же если $x_0=\sup M$ , то существует неубывающая последовательность точек ${x_1\leqslant x_2\leqslant \dots\leqslant x_i\leqslant \dots}$ , которая стремится к .

Если точка $x_0=\inf M$ принадлежит множеству , то является наименьшим элементом этого множества: $x_0=\min M$ ; аналогично, если $x_0=\sup M\in M$ , то $x_0=\max M$ .

Кроме того, для дальнейшего нам понадобится следующая

Лемма 3.1 Пусть - непрерывная функция на отрезке , и множество тех точек $x\in[a;b]$ , в которых (или $f(x)\leqslant K$ , или $f(x)\geqslant K$ ) не пусто. Тогда в множестве имеется наименьшее значение $x_{\min}\in M$ , такое что $x\geqslant x_{\min}$ при всех $x\in M$ .

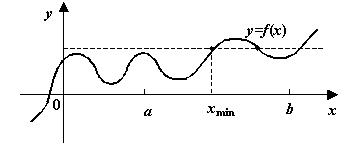
Рис.3.22. Наименьший аргумент, при котором функция принимает заданное значение

Доказательство. Поскольку - ограниченное множество (это часть отрезка ), то оно имеет точную нижнюю грань $x_0=\inf M$ . Тогда существует невозрастающая последовательность $\{x_i\}\sbs M$ , $i=1,2,\dots$ , такая что $x_i\to x_0$ при $i\to\infty$ . При этом , по определению множества . Поэтому, переходя к пределу, получаем, с одной стороны,

$\displaystyle \lim\limits_{i\to\infty}f(x_i)=\lim_{i\to\infty}K=K,$

а с другой стороны, вследствие непрерывности функции ,

$\displaystyle \lim\limits_{i\to\infty}f(x_i)=f(x_0).$

Значит, , так что точка принадлежит множеству и $x_0=\min M$ .

В случае, когда множество задано неравенством $f(x)\leqslant K$ , мы имеем $f(x_i)\leqslant K$ при всех $i=1,2,\dots$ и по теореме о переходе к пределу в неравенстве получаем

$\displaystyle \lim\limits_{i\to\infty}f(x_i)\leqslant K,$

откуда $f(x_0)\leqslant K$ , что означает, что $x_0\in M$ и $x_0=\min M$ . Точно так же в случае неравенства $f(x)\geqslant K$ переход к пределу в неравенстве даёт

$\displaystyle \lim\limits_{i\to\infty}f(x_i)\geqslant K,$

откуда $f(x_0)\geqslant K$ , $x_0\in M$ и $x_0=\min M$ .

Теорема 3.8 (об ограниченности непрерывной функции) Пусть функция непрерывна на отрезке . Тогда ограничена на , то есть существует такая постоянная , что $\vert f(x)\vert\leqslant K$ при всех $x\in[a;b]$ .

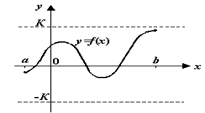
Рис.3.23. Непрерывная на отрезке функция ограничена

Доказательство. Предположим обратное: пусть не ограничена, например, сверху. Тогда все множества ${M_1=\{x\in[a;b]:f(x)\geqslant f(a)+1\}}$ , ${M_2=\{x\in[a;b]:f(x)\geqslant f(a)+2\},\dots}$ , ${M_i=\{x\in[a;b]:f(x)\geqslant f(a)+i\},\dots}$ , не пусты. По предыдущей лемме в каждом из этих множеств имеется наименьшее значение , $i=1,2,\dots$ . Покажем, что

$\displaystyle x_0=a<x_1<x_2<\dots<x_i<\dots.$

Действительно, . Если какая-либо точка из $x_2,x_3,\dots$ , например , лежит между и , то

$\displaystyle f(x_0)=f(a)<f(x_1)=f(a)+1<f(x_i)=f(a)+i,$

то есть - промежуточное значение между и . Значит, по теореме о промежуточном значении непрерывной функции, существует точка $x_*\in(x_0;x_i)$ , такая что , и $x_*\in M_1$ . Но , вопреки предположению о том, что - наименьшее значение из множества . Отсюда следует, что при всех $i\geqslant 2$ .

Точно так же далее доказывается, что при всех $i\geqslant 3$ , при всех $i\geqslant 4$ , ит.д. Итак, $\{x_i\}$ - возрастающая последовательность, ограниченная сверху числом . Поэтому существует $\lim\limits_{i\to\infty}x_i=x'$ . Из непрерывности функции следует, что существует $\lim\limits_{i\to\infty}f(x_i)=f(x')$ , но $f(x_i)=f(a)+i\to+\infty$ при $i\to\infty$ , так что предела не существует. Полученное противоречие доказывает, что функция ограничена сверху.

Аналогично доказывается, что ограничена снизу, откуда следует утверждение теоремы.

Очевидно, что ослабить условия теоремы нельзя: если функция не является непрерывной, то она не обязана быть ограниченной на отрезке (приведём в качестве примера функцию

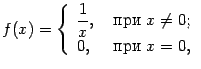
$\displaystyle f(x)=\left\{\begin{array}{ll}\dfrac{1}{x},&\mbox{ при }x\ne0;\\0,&\mbox{ при }x=0,\end{array}\right.$

на отрезке . Эта функция не ограничена на отрезке, так как при имеет точку разрыва второго рода, такую что $\vert f(x)\vert\to+\infty$ при $x\to0$ . Также нельзя заменить в условии теоремы отрезок интервалом или полуинтервалом: в качестве примера рассмотрим ту же функцию на полуинтервале . Функция непрерывна на этом полуинтервале, но неограничена, вследствие того что $f(x)\to+\infty$ при $x\to0+$ .

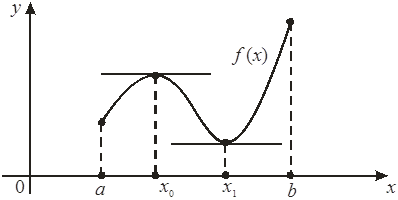
Поиск наилучших постоянных, которыми можно ограничить функцию сверху и снизу на заданном отрезке, естественным образом приводит нас к задаче об отыскании минимума и максимума непрерывной функции на этом отрезке. Возможность решения этой задачи описывается следующей теоремой.

Теорема 3.9 (о достижении экстремума непрерывной функцией) Пусть функция непрерывна на отрезке . Тогда существует точка $x_*\in[a;b]$ , такая что $f(x_*)\leqslant f(x)$ при всех $x\in[a;b]$ (то есть - точка минимума: $f(x_*)=\min\limits_{x\in[a;b]}f(x)$ ), и существует точка $x_{**}\in[a;b]$ , такая что $f(x_{**})\geqslant f(x)$ при всех $x\in[a;b]$ (то есть $x_{**}$ - точка максимума: $f(x_{**})=\max\limits_{x\in[a;b]}f(x)$ ). Иными словами, минимальное и максимальное⁸ значения непрерывной функции на отрезке существуют и достигаются в некоторых точках и $x_{**}$ этого отрезка.

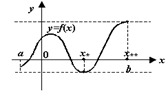
Рис.3.24. Непрерывная на отрезке функция достигает максимума и минимума

Доказательство. Так как по предыдущей теореме функция ограничена на сверху, то существует точная верхняя грань значений функции на - число $K=\sup\limits_{x\in[a;b]}\{f(x)\}$ . Тем самым, множества $M_1=\{x\in[a;b]:f(x)\geqslant K-1\}$ , ${M_2=\{x\in[a;b]:f(x)\geqslant K-\frac{1}{2}\}}$ ,..., $M_i=\{x\in[a;b]:f(x)\geqslant K-\frac{1}{i}\}$ ,..., не пусты, и по предыдущей лемме в них есть наименьшие значения : $f(x_i\geqslant K-\frac{1}{i}$ , $i=1,2,\dots$ . Эти не убывают (доказывается это утверждение точно так же, как в предыдущей теореме):

$\displaystyle x_1\leqslant x_2\leqslant x_3\leqslant \dots\leqslant x_i\leqslant \dots,$

и ограничены сверху числом . Поэтому, по теореме о пределе монотонной ограниченной последовательности, существует предел $\lim\limits_{i\to\infty}x_i=x_{**}.$ Так как $f(x_i)\geqslant K-\frac{1}{i}$ , то и

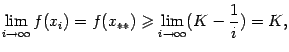
$\displaystyle \lim\limits_{i\to\infty}f(x_i)=f(x_{**})\geqslant\lim\limits_{i\to\infty}(K-\frac{1}{i})=K,$

по теореме о переходе к пределу в неравенстве, то есть $f(x_{**})\geqslant K$ . Но при всех $x\in[a;b]$ $f(x)\leqslant K$ , и в том числе $f(x_{**})\leqslant K$ . Отсюда получается, что $f(x_{**})=K$ , то есть максимум функции достигается в точке $x_{**}$ .

Аналогично доказывается существование точки минимума.

В этой теореме, как и в предыдущей, нельзя ослабить условия: если функция не является непрерывной, то она может не достигать своего максимального или минимального значения на отрезке, даже будучи ограниченной. Для примера возьмём функцию

$\displaystyle f(x)=\left\{\begin{array}{ll}1+x,&\mbox{ при }x\in[-1;0);\\0,&\mbox{ при }x\in[0;1],\end{array}\right.$

на отрезке . Эта функция ограничена на отрезке (очевидно, что $\vert f(x)\vert\leqslant 1$ ) и $\sup\limits_{x\in[-1;1]}\{f(x)\}=1$ , однако значение1 она не принимает ни в одной точке отрезка (заметим, что , а не 1). Дело в том, что эта функция имеет разрыв первого рода в точке , так что при $x\to0-$ предел не равен значению функции в точке0. Далее, непрерывная функция, заданная на интервале или другом множестве, не являющемся замкнутым отрезком (на полуинтервале, полуоси) также может не принимать экстремального значения. В качестве примера рассмотрим функцию на интервале . Очевидно, что функция непрерывна и что $\inf\limits_{x\in(0;1)}=0$ и $\sup\limits_{x\in(0;1)}=1$ , однако ни значения0, ни значения1 функция не принимает ни в какой точке интервала . Рассмотрим также функцию $f(x)=\mathop{\rm arctg}\nolimits x$ на полуоси $[0;+\infty)$ . Эта функция непрерывна на $[0;+\infty)$ , возрастает, принимает своё минимальное значение0 в точке , но не принимает ни в какой точке максимального значения (хотя ограничена сверху числом $\dfrac{\pi}{2}$ и $\sup\limits_{x\in[0;+\infty)}f(x)=\dfrac{\pi}{2}).$

Раздел: Математика
Количество знаков с пробелами: 10670
Количество таблиц: 0
Количество изображений: 7

Скачать

... [a,b]. Теперь мы можем рассматривать функции в произвольных нормированных пространствах. III. Методы аппроксимации 3.1 Приближение функций многочленами. Алгебраическим многочленом степени n называется функция - действительные числа, называемые коэффициентами. Алгебраические многочлены являются простейшими функциями. Они непрерывны при любом x. Производная многочлена- так же многочлен, степень ...

Скачать

... , дифференцировании и других действиях с функциями. На практике часто применяется разложение функций в степенной ряд. Ряд Тейлора. (Пьер Альфонс Лоран (1813 – 1854) – французский математик) Функция f(z), аналитическая в круге , разлагается в сходящийся к ней степенной ряд по степеням (z – z0). Коэффициенты ряда вычисляются по формулам: Степенной ряд с коэффициентами такого вида называется рядом ...

Скачать

... b). Тогда, если f'(x) > 0, х Î (a, b), то f(x) строго монотонно возрастает на (a, b). Если же f'(x) < 0, х Î (a, b), то f(x) строго монотонно убывает на (a, b). 2. ИССЛЕДОВАНИЕ ФУНКЦИЙ 2.1 Достаточные условия экстремума функции В лекции 1 мы рассмотрели основные теоремы математического анализа, которые широко используются при исследовании функции, построении ее графика. ...

Скачать

... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

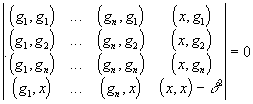
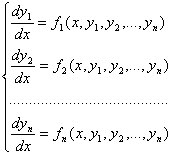
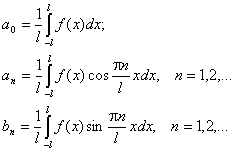
0 комментариев

Разделы

Инфо

Следите за новостями