Навигация
Определение. Сумма членов бесконечной числовой последовательности ![]() называется числовым рядом.
называется числовым рядом.
![]()
При этом числа ![]() будем называть членами ряда, а un – общим членом ряда.
будем называть членами ряда, а un – общим членом ряда.
Определение. Суммы ![]() , n = 1, 2, … называются частными (частичными) суммами ряда.
, n = 1, 2, … называются частными (частичными) суммами ряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, …
Определение. Ряд ![]() называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
![]()
Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов.1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
2) Рассмотрим два ряда ![]() и
и ![]() , где С – постоянное число.
, где С – постоянное число.
Теорема. Если ряд ![]() сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд ![]() тоже сходится, и его сумма равна СS. (C ¹ 0)
тоже сходится, и его сумма равна СS. (C ¹ 0)
3) Рассмотрим два ряда ![]() и
и ![]() . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд ![]() , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды ![]() и
и ![]() сходятся и их суммы равны соответственно S и s, то ряд
сходятся и их суммы равны соответственно S и s, то ряд ![]() тоже сходится и его сумма равна S + s.
тоже сходится и его сумма равна S + s.
![]()
Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Критерий Коши.(необходимые и достаточные условия сходимости ряда)
Для того, чтобы последовательность ![]() была сходящейся, необходимо и достаточно, чтобы для любого
была сходящейся, необходимо и достаточно, чтобы для любого ![]() существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
![]() .
.
1.3 Определение. Ряд ![]() называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной сходимости ряда ![]() необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
![]()
выполнялось бы для всех х на отрезке [a,b].
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд ![]() сходится равномерно и притом абсолютно на отрезке [a,b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
сходится равномерно и притом абсолютно на отрезке [a,b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
![]()
т.е. имеет место неравенство:
![]() .
.
Еще говорят, что в этом случае функциональный ряд ![]() мажорируется числовым рядом
мажорируется числовым рядом ![]() .
.
ряд ![]() называется положительным, если Un≥0, для всех n ? N
называется положительным, если Un≥0, для всех n ? N
Интегральный признак Коши.
Если j(х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j(1) + j(2) + …+ j(n) + … = ![]() и несобственный интеграл
и несобственный интеграл ![]() одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Пример. Ряд ![]() сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл
сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл ![]() сходится при a>1 и расходится a£1. Ряд
сходится при a>1 и расходится a£1. Ряд ![]() называется общегармоническим рядом.
называется общегармоническим рядом.
Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b] и ![]() то интегралы
то интегралы 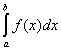 и
и 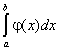 ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости.
Определение. Степенным рядом называется ряд вида
![]() .
.
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Пример. Исследовать на сходимость ряд ![]()
Применяем признак Даламбера:
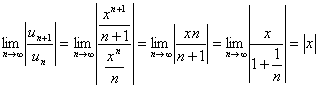 .
.
Получаем, что этот ряд сходится при ![]() и расходится при
и расходится при ![]() .
.
Теперь определим сходимость в граничных точках 1 и –1.
При х = 1: ![]() ряд сходится по признаку Лейбница (см. Признак Лейбница. ).
ряд сходится по признаку Лейбница (см. Признак Лейбница. ).
При х = -1: ![]() ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд).
Похожие работы
Ось абсцисс пустим вдоль оси первого конуса, ось ординат - вдоль оси второго конуса, ось аппликат - параллельно оси цилиндра, причем так, чтобы система координат была правой. Расстояние d от вершин конусов до начала координат находим с помощью Теоремы Пифагора:2 + l = + 2 = 7.7 (см) таким образом ось цилиндра описывается следующим уравнением: Вершина первого конуса имеет следующие координаты - ...
урецкий, персидский, татарский и французский языки, а также мусульманское и международное право. Целью данной работы является освещение предмета высшей математики в профессиональной деятельности военного юриста. Работа включает не только теоретические аспекты применения методов высшей математики в военной юриспруденции, но и примеры практического использования методик. 1. Характеристика ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
бнику, решения задач необходимо ответить на вопросы для самопроверки, помещенные в конце темы. В соответствии с действующим учебным планом студенты-заочники изучают курс высшей математики в течение 1 и 2 семестра и выполняют в каждом семестре по две контрольные работы. Первая и вторая контрольные работы выполняются студентами в 1 семестре после изучения тем 1-2 и 3-4 соответственно. Третья и ...


0 комментариев