Навигация
Вибірковий метод та його значення для вивчення правових явищ
Міністерство освіти і науки України
Курсова робота
на тему Вибірковий метод та його значення для вивчення правових явищ
Харків 2011
Зміст
Вступ
1. Основні поняття теорії ймовірності
2. Поняття закону великих чисел
3. Вибірковий метод та його значення для вивчення правових явищ
4. Основні положення вибіркового спостереження
5. Способи відбору одиниць у вибіркову сукупність
Висновки
Список літератури
Вступ
У своїй практичній діяльності ми завжди зустрічаємося з явищами, результат яких важко, а інколи і зовсім неможливо передбачати наперед, тому що наслідки їх залежать від випадку. Наприклад, який застрахований об`єкт буде знищено внаслідок стихійного лиха – діло випадку. Але страхові органи керуються в своїй діяльності передбаченням не кожного окремого об`єкта, а їх значної кількості. При вивченні їх у великій кількості можна передбачити їх стан у майбутньому. Тому при статистичній обробці емпіричних даних використовують певні визначення і правила, які встановлені теорією ймовірності.
Теорія ймовірності – це математична наука, яка виникла всередині ХУП сторіччя. Прийнято першими роботами, в яких народилися основні поняття теорії ймовірності, вважати роботи французів Б. Паскаля (1623 – 1662), Фермі П. (1601 – 1665) і голландця Х. Гюйгенса (1629 – 1695). Подальший розвиток теорії ймовірності пов`язують з ім`ям швейцарського математика Я.Бернуллі (1654 – 1705), який в тракті “Ars Conjectandi”, надрукованому в 1713 р., вперше в елементарному вигляді доказав теорему, яка в подальшому була названа законом великих чисел.
В ХІХ сторіччі теорія ймовірності починає з успіхом застосовуватися в страховій справі, статистиці народонаселення, у біології і військових науках, особливо в артилерії. В цей період теорія ймовірності збагачуються працями француза П. Лапласа (1749 – 1827), німця К. Гауса (1777 – 1855), француза С.Пуассон (1784 – 1840) та інших.
Значний вклад в розвиток теорії ймовірності внесено російським вченим П. Л. Чебишевим (1821 – 1894) та його учнями А.А.Марковим (1892 – 1922) і О.М.Ляпуновим (1857 – 1918). Своїми працями вони перетворили теорію ймовірності в систематизовану і чітку математичну науку.
1. Основні поняття теорії ймовірності
Зараз вона використовується у всіх галузях знань, де досліджуються прояви випадкових явищ з стійкою частістю. Наприклад, народжуваність дівчат або хлопчаків на певній території за тривалий проміжок часу.
Теорія ймовірності – це розділ математики, в якому вивчаються тільки випадкові явища (події) з стійкою частістю і встановлюються закономірності при масовому їх повторенні.
Одне з головних визначень теорії ймовірності – це поняття події. Явища, які розглядаються з точки зору, здійснилися вони чи ні, називають подіями. Стосовно до подій ставиться така основна задача: передбачити, чи з`явиться (здійсниться) досліджувана подія при настанні того чи іншого наперед заданого комплексу факторів.
Якщо при даному комплексі факторів обов`язково відбудеться подія, то вона має назву достовірної події. Якщо при даному комплексі факторів подія не може відбутися, то вона має назву неможливої події.
Якщо при даному комплексі факторів подія може відбутися або не відбутися, то вона має назву випадкової події. Інакше кажучи, подія називається випадковою, якщо вона однозначно не визначається умовами, в яких вона протікає, або ми не можемо врахувати всі фактори, які впливають на подію. Наука, яка вивчає закономірності масових випадкових подій, і називається теорією ймовірностей.
Прикладом випадкових подій – народжуваність хлопчика (або дівчини) у конкретній сім`ї; кількість злочинів, вчинених за певний проміжок часу. Кожний окремий злочин – унікальне соціально-стихійне діяння по протиправному вирішенні протиріч між людиною і суспільством. Тому ми ніколи не зможемо з абсолютною достовірністю визначити де, хто і коли вчинить той чи інший злочин. Злочинність є дзеркалом, у якому ми можемо більш-менш об'єктивно бачити, як функціонує наше суспільство, тому рівень зареєстрованих злочинів є вирішальним фактором при оцінці якості нашого життя.
Застосовувати теорію ймовірності можна лише у тих випадках, коли ми в силу об`єктивних причин не можемо абсолютно точно знати про умови, походження та розвиток явища. Теорія ймовірності описує лише ті випадкові події, яким притаманні стійкі частості. Причому чим в менших межах коливаються частості вихідних подій, тим більш точніше теорія ймовірності опише досліджуване явище.
Одне із основних понять – це ймовірність. Існують різні підходи щодо визначення цього поняття. Класичне визначення ймовірності таке: ймовірність випадкової події дорівнює відношенню числа випадків, які сприяють події, до спільного числа можливих випадків. Інакше кажучи, для значної кількості іспитів ймовірність характеризує частість події.
Кожна подія має числову характеристику у вигляді ймовірності. Ймовірність завжди знаходиться у межах від 0 до 1 (або у відсотках від 0 до 100%), ймовірність випадкової події завжди знаходиться між 0 та 1, тобто ніколи не дорівнює ні 1, ні 0. Тому, що якщо ймовірність буде дорівнювати 1, то в цьому випадку ми кажемо про вірогідність. Нас же цікавить ймовірність події, яка буде наближуватися до 1, але ні в якому випадку ймовірність випадкової події не може дорівнювати 1.
Величина випадкової події характеризується випадковою величиною, яка приймає якесь одне значення із деякої множини можливих значень. Але яким буде це значення, заздалегідь сказати не можна. Інакше кажучи, випадкова величина має цілий набір припустимих значень і в результаті кожного експерименту набуває лише якогось одного з них.
Найбільш поширений приклад: випадання герба при підкиданні монети. Зрозуміло, що може бути або герб, або ні. Відомо, що французький вчений Буфон наприкінці ХУШ сторіччя провів експеримент з підкиданням монети 4040 разів, при цьому 2028 разів випад герб, а 2012 – ні. Тобто в його експерименті частість випадання герба дорівнювала 0,5069 (2028 / 4040) при ймовірності 0,5000 (1/2).
Англійський вчений К. Пирсон провів 2 експерименти: перший раз він підкидав монету 12 тисяч разів, другий – 24 тисячі разів. При першому експерименті він отримав частість 0,5016, а при другому – 0,5005.
Усе це свідчить, що при збільшенні кількості спостережень частість усе менше відрізняється від ймовірності.
Похожие работы
... ій сугестії індивіда, невпевненості в собі тощо. За ознакою "усвідомлювання - неусвідомлювання" виокремлюють усвідомлювані (переконання, групові експектації, вплив авторитету) та неусвідомлювані механізми десоціалізації (вони проявляються здебільшого в ранньому дитинстві та виражаються через такі явища, як навіювання, наслідування, психологічне зараження, ідентифікація). Соціальне оточення діє на ...
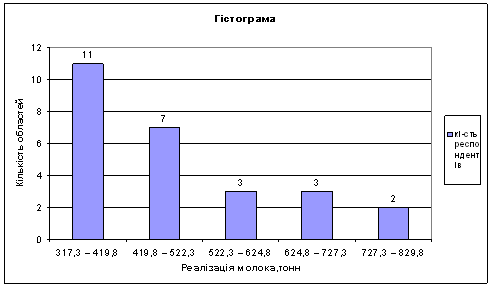
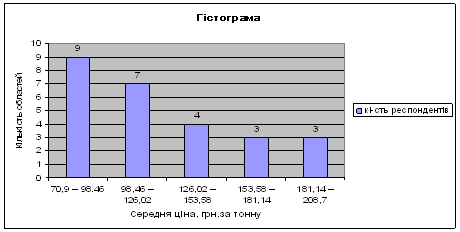
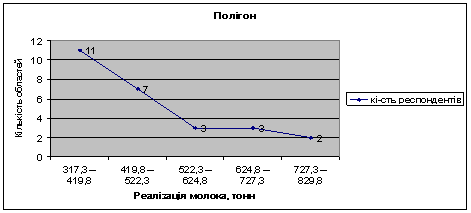
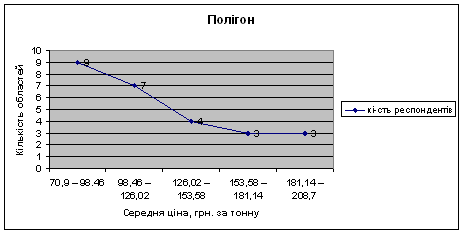
... : факторну і результативну. Факторною називається така ознака, під впливом якої змінюється інша ознака, що називається результативною. У табл.2.1.1 наведено статистичне вивчення виручки від реалізації молока Таблиця 2.1.1. Статистичне вивчення виручки від реалізації молока № Виробництво тонн Ціна за 1 тонну Виручка від реалізації, тис.грн 1 362,1 95,9 34,73 2 359,6 91,4 32,87 3 ...
... інформації. До основних методів належать: метод масових спостережень, групувань, відносних, середніх величин, графічний, індексний, кореляційний, балансовий. Методи статистики пов’язані з етапами статистичного дослідження: статистичне спостереження; зведення та групування даних спостереження; обчислення узагальнюючих показників та їх аналіз. Щоб правильно і своєчасно впливати на процеси, що ві ...
... іки можна за даними торгових звітів скласти необмежене число графіків і таблиць, які використовуються керівництвом підприємства для ефективного прийняття рішення.2. Аналіз діяльності вивчення попиту і прогнозування збуту продукції на підприємстві 2.1 Загальна характеристика підприємства Відомості про підприємство та характеристика продукції. ПП «Компік» створене у в 2002 р. Відомості про ...

0 комментариев