Динаміка урожайності

2.3 Динаміка урожайності

Аналіз рядів динаміки має за мету вивчення зміни явища за часом і встановлення його напрямку, характеру цієї зміни і вияв закономірності розвитку. Для оцінювання властивостей динаміки у статистиці застосовуються взаємопов’язані показники, або аналітичні показники.

У процесі аналізу динаміки суспільних явищ визначають абсолютний приріст, темпи зростання, приросту, абсолютне значення 1% приросту на основі порівняння рівнів ряду динаміки. За базу порівняння беруть попередній, або початковий рівень динаміки.

Абсолютній приріст показує на скільки одиниць підвищився або зменшився поточний рівень порівняно з базисним, тобто за той чи інший період часу.

де П – абсолютний приріст за t-у одиниць часу;

у_i - порівнюваний рівень;

y_i-t - базисний рівень.

Якщо за базу порівняння взяти попередній рівень, матимемо таку формулу ланцюгових абсолютних приростів:

де y_і-1 - рівень попереднього періоду відносно порівнюваного.

Темп зростання показує, у скільки разів збільшився порівнюваний рівень відносно базисного.

Якщо за базу порівняння взяти попередній рівень, дістаємо ланцюгові темпи зростання.

Між ланцюговими і базисними темпами зростання, вираженими у вигляді коефіцієнтів, є певний взаємозв'язок. Добуток послідовних ланцюгових темпів зростання дорівнює базисному темпу зростання за відповідний період і, навпаки, поділивши наступний базисний темп зростання на попередній, матимемо відповідний ланцюговий темп зростання. [14, с. 212-214]

Темп приросту становить відношення абсолютного приросту до базисного рівня

Темп приросту можна визначити також відніманням від темпів зростання величини 100 або 1.

Абсолютне значення 1% приросту дорівнює відношенню абсолютного приросту до темпу приросту за той самий період.

де А – абсолютна величина 1% приросту.

Всі розраховані показники ряду динаміки занесемо в таблицю 2.3.1

 

Таблиця 2.3.1

Показники ряду динаміки картоплі

Роки	Урожайність, ц/га	Абсолютний приріст		Коефіцієнт росту		Темп росту, %		Темп приросту, %		Абсолютне значення 1% приросту
		Базисний	Щорічний	Базисний	Щорічний	Базисний	Щорічний	Базисний	Щорічний
1998	72	-	-	1.000	1.000	1.000	1.000	-	-	-
1999	82	10	10	1,14	1,14	113,89	113,89	13,89	13,89	0,72
2000	95	23	13	1,32	1,16	131,94	115,85	31,94	1,96	6,62
2001	66	-6	-29	0,92	0,69	91,67	69,47	-8,33	-46,38	0,63
2002	75	3	9	1,04	1,14	104,17	113,64	4,17	44,16	0,20
2003	82	10	7	1,14	1,09	113,89	109,33	13,89	-4,30	-1,63
2004	98	26	16	1,36	1,20	136,11	119,51	36,11	10,18	1,57
2005	85	13	-13	1,18	0,87	118,06	86,73	18,06	-32,78	0,40
2006	77	5	-8	1,07	0,91	106,94	90,59	6,94	3,85	-2,08
2007	34	-3	6	0,91	1,21	91	121	-9	21	0,28
2008	39	2	5	1,054	1,14	105,4	114	5,4	14	0,36

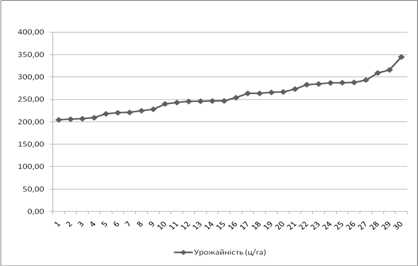
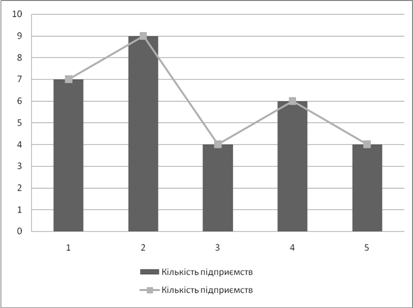
Відобразимо динамічний ряд графічно (рисунок 2.3. 1):

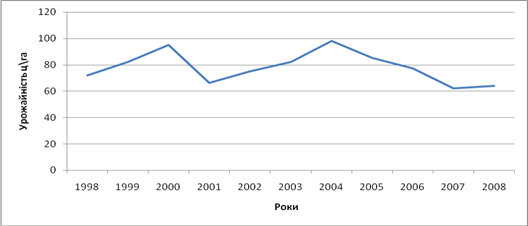
Рис. 2.3.1 – Фактичний рівень ряду динаміки

Для узагальнення характеристики вихідних рівнів та розрахункових величин ряду динаміки слід визначити середні показники:

Середній рівень інтервального ряду з рівним інтервалом розраховують за формулою:

,

Де n – загальне число рівнів ряду динаміки;

Середній абсолютний приріст розраховується за формулою середньої арифметичної простої:

,

Середній коефіцієнт обчислюється за формулою:

,

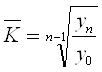Для визначення основної тенденції розвитку в рядах динаміки є кілька способів їх обробки.

Укрупнення періодів – найпростіший спосіб обробки рядів динаміки. Суть його полягає в тому, що дані динамічного ряду об’єднують у групи за періодами (триріччя, п'ятиріччя, десятиріччя) тощо.

Прийом укрупнення періодів та згладжування ряду динаміки за допомогою ковзної середньої.

 

Таблиця 2.3.2

Аналіз ряду динаміки методом періодів та ковзної середньої

Роки	Урожайність, ц/га	Період	Суми по трьох роках	Середнє по трьох роках	Період	Суми по трьох роках	Середні ковзні
1998	72	1998-2000	249	83	-	-	-
1999	82				1998-2000	249	83
2000	95				1999-2001	243	81
2001	66	2001-2003	223	74,33	2000-2002	236	78,67
2002	75				2001-2003	223	74,33
2003	82				2002-2004	255	85
2004	98	2004-2006	260	86,67	2003-2005	265	88,33
2005	85				2004-2006	260	86,67
2006	77				2005-2007	224	74,67
2007	62	2007-2008	126	63	2006-2008	203	67,67
2008	64				-	-	-

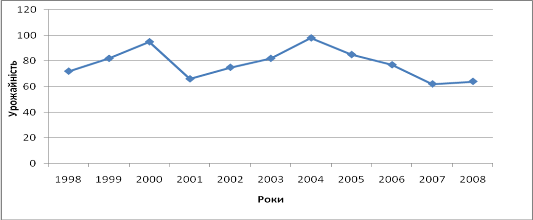
Рис. 2.3.2 – Вирівнювання ряду динаміки методом укрупнення періодів

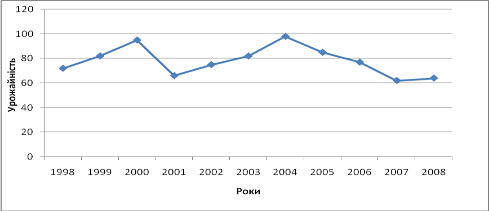
Рис. 2.3.3 - Вирівнювання ряду динаміки методом ковзної середньої

Проведемо вирівнювання ряду динаміки по середньому абсолютному приросту та по середньому коефіцієнту росту. Для початку розрахуємо значення абсолютного приросту.

Знайдемо середній коефіцієнт зростання

К==

 

Вирівнювання ряду динаміки за середнім абсолютним приростом. На основі середнього абсолютного приросту можна провести вирівнювання ряду динаміки за формулою:

,

де - вирівняні рівні;

- початковий рівень розподілу;

- середній абсолютний приріст;

t – порядковий номер року.

Таблиця 2.3.3

Аналіз ряду динаміки методом вирівнювання за середнім абсолютним приростом

Роки	Порядковий номер року	Урожайність, ц/га	Вирівнювання за середнім абсолютним приростом	Відхилення фактичного рівня від розрахункового
	t
1998	0	72	72	0
1999	1	82	71,2	10,8
2000	2	95	70,4	24,6
2001	3	66	69,6	-3,6
2002	4	75	68,8	6,2
2003	5	82	60	14
2004	6	98	67,2	30,8
2005	7	85	66,4	18,6
2006	8	77	65,6	11,4
2007	9	62	64,8	-2,8
2008	10	64	64	0

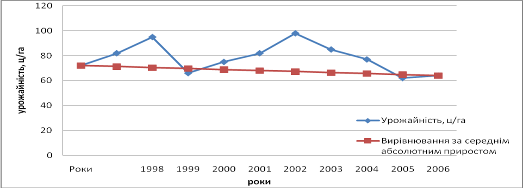
Рис. 2.3.4 – Вирівнювання динамічного ряду за середнім абсолютним приростом

Вирівнювання ряду динаміки за середнім коефіцієнтом зростання обчислюється за формулою:

Занесемо дані в таблицю 2.3.4

Таблиця 2.3.4

Аналіз ряду динаміки методом вирівнювання за середнім коефіцієнтом росту

Роки	Порядковий номер року	Урожайність, ц/га	Вирівнювання за середнім коефіцієнтом зростання	Відхилення фактичного рівня від розрахункового
	t
1998	0	72	72	0
1999	1	82	71,73	10,27
2000	2	95	71,47	23,53
2001	3	66	71,2	-5,2
2002	4	75	70,94	4,06
2003	5	82	70,68	11Ю32
2004	6	98	70,42	27,58
2005	7	85	70,16	14,84
2006	8	77	69,9	7,1
2007	9	62	69,64	-7,64
2008	10	64	69,38	-5,38

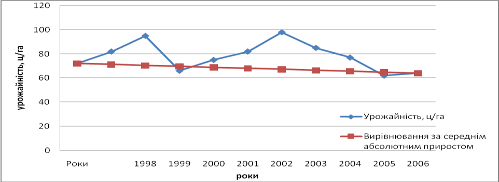
Рис. 2.3.5 – Вирівнювання ряду динаміки за середнім коефіцієнтом зростання

Вирівнювання динамічного ряду за способом найменших квадратів:

Спосіб найменших квадратів – знаходження такої математичної лінії, ординати точок якої були б найближчі до фактичних значень ряду динаміки.

Для прояву тенденції ряду можна використати рівняння прямої:

,

Де , - невідомі параметри рівняння,

t – порядковий номер року

Спочатку необхідно скласти систему з двох нормальних рівнянь:

 

Але для розрахунку ці рівняння можна спростити, оскільки :

;

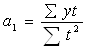
Знаходять коефіцієнт , .[5, с. 87-93]

 

Таблиця 2.3.5

Фактичний і розрахунковий рівень динамічного ряду способом найменших квадратів

Роки	Урожайність, ц/га	Відхилення від року, який займає центральне положення	Розрахункові величини для визначення параметрів рівняння		Приріст розрахований по рівнянні прямої	Відхилення фактичного приросту від розрахованого по рівнянню прямої
	y	t		yt
1998	72	-5	25	-360	83,14	-11,14	124,02
1999	82	-4	16	-328	82,11	-0,11	0,01
2000	95	-3	9	-285	81,08	13,92	193,72
2001	66	-2	4	-132	80,05	-14,05	197,53
2002	75	-1	1	-75	79,03	-4,03	16,22
2003	82	0	0	0	78,00	4,00	16,00
2004	98	1	1	98	76,97	21,03	442,15
2005	85	2	4	170	75,95	9,05	81,98
2006	77	3	9	231	74,92	2,08	4,33
2007	62	4	16	248	73,89	-11,89	141,39
2008	64	5	25	320	72,86	-8,86	78,56

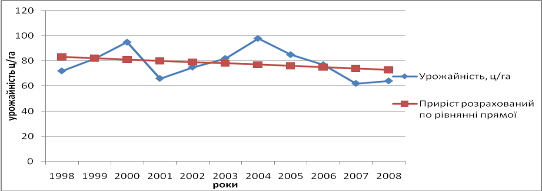
Рис. 2.3.6 – Вирівнювання динамічного ряду методом найменших квадратів

Аналіз рядів динаміки має за мету вивчення зміни явища за часом і встановлення його напрямку, характеру цієї зміни і вияв закономірності розвитку. Для оцінювання властивостей динаміки у даній роботі використовувались взаємопов’язані показники, або аналітичні показники.

У процесі аналізу динаміки урожайності картоплі я використовувала абсолютний приріст, темпи зростання, приросту, абсолютне значення 1% приросту на основі порівняння рівнів ряду динаміки. За базу порівняння берала попередній, або початковий рівень динаміки.

В цілому дослідження показало що динаміка урожайності картоплі має тенденцію до зростання.

 

2.4 Індексний аналіз

У статистистичній практиці часто виникає потреба у визначенні не тільки темпів розвитку окремого явища, а й середніх темпів розвитку кількох різнорідних явищ. Так, аналізуючи гослодарську діяльність підприємства, визначають, як змінилися обсяг виробництва валової продукції, ціни реалізації, продуктивності праці порівняно з минулими роками, планом або іншими підприємствами і т.д. Для цього застосовують індекси (від лат. “index” – показники). [10, с. 15-23]

У широкому розумінні індекс – це символ або число, яким позначається окремий елемент масиву (класифікація). Індексом у статистиці називається відносний показник що характеризує зміну рівня cоціально-економічного явища в часі порівняно з планом або в просторі.

Індекси використовують не лише для визначення загальної зміни складного явища у часі або просторі, а й для виявлення впливу окремих факторів, які зумовили цю зміну. [12, с. 150-154]

За допомогою індексного методу аналізу оцінюють вплив окремих факторів на зміну результативного показника у відносному і абсолютному виразі. Для індексного аналізу факторів використовують лише ті індекси, які економічно взаємопов’язані .

Щоб докладно висвітлити характер розвитку соціально – економічних явищ і проаналізувати його, статистика використовує систему індексів.В даному проекті ми застосовували індекси якісних показників, які відображають зміни ознак , властивостей одиниць сукупності.

За ступенем охоплення елементів сукупності індекси поділяють на індивідуальні та загальні.

Індивідуальні індекси показують зміну одного елемента або всієї однорідної сукупності. [7, с. 65-71]

Якщо індивідуальний індекс позначити через і, продукцію звітного періоду в натуральному вигляді – через q₁, а базисного – через q₀, то індивідуальний індекс фізичного обсягу продукції матиме вигляд:

,

де - фізичний об’єм продукції звітного року;

- фізичний об’єм продукції базисного року.

Загальний індекс фізичного об’єму продукції визначають за формулою:

,

де - фізичний об’єм продукції звітного року;

Для побудови загального індексу необхідно визначити такі співмірники (ваги), за допомогою яких несумірні елементи можна довести до сумірного вигляду. Основною формою загального індексу є агрегатний.

Зведений індекс кількості проданої продукції, або як його ще називають індекс фізичного обсягу товарообороту, має вигляд:

Загальні індекси цін, собівартості, продуктивності праці одного виду продукції, але віднесеного до різних об'єктів, можна обчислити двома способами – як індекси фіксованого (постійного) і змінного окладу.

Індекси, в яких змінюється одна величина, називають індексами фіксованого окладу, їх визначають як звичайні агрегатні індекси:

Індекси змінного складу є відношенням середніх рівнів явища що досліджується.

На величину індексів змінного складу впливають зміни не тільки рівня явища, а й структури сукупності.

Існує система взаємопов’язаних індексів аналізу динаміки середнього рівня.

Використовуючи індексний метод, проаналізуєм зміни урожайності картоплі (таблиця 2.4.1).

 

Таблиця 2.4.1

Індексний аналіз урожайності картоплі

Підприємство	Площа, га		Урожайність, ц/га		Розрахункові дані
	базисний період q0	звітний період q1	базисний період z0	звітний період z1	q0z0	q1z1	q1z0	q0z1
1.	105	120	106	106	11130	12720	12720	11130
2.	119	123	108	109	12852	13407	13284	12971
3.	125	122	121	117	15125	14274	14762	14625
Всього	349	365	335	332	39107	40401	40766	38726

Приріст (збільшення) урожайності визначають як різницю між урожайністю у звітному і базисному періодах:

1294(ц)

у тому числі за рахунок зміни посівних площ:

1659(ц)

зміни урожайності:

-365 (ц)

Фіксований індекс валового збору витрат обчислюють за такою формулою:

=0,99=99%

 

Отже урожайність в середньому на всіх посівних площах зменшилась на1%

-  Індекс змінного складу, тобто індекс валового збору витрат за рахунок посівної площі:

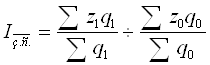-  =0,98=98%

 

Отже урожайність на всіх посівних площах зменшилась на 2%.

Індекс структурних зрушень

=0,99*0,98=0,97

 

Отже середня урожайність посівних площ зменшилась на 1% причому така зміна відбулась за рахунок впливу факторів у звітному періоді:

1)  Зниження урожайності посівних площ в середньому на 2%

2)  Зменшення посівних площ в середньому призвело до зменшення урожайності на 3%.

РОЗДІЛ 3

ПРОГНОЗУВАННЯ УРОЖАЙНОСТІ КАРТОПЛІ

Прогнозування – процес наукового виявлення можливих шляхів і результатів майбутнього розвитку соціально-економічних явищ, оцінка показників, що характеризують ці явища для більш або менш віддаленого майбутнього.

Приблизне визначення відсутніх рівнів у середині одно якісного періоду, коли відомі рівні,що лежать по обидві сторони невідомого, називають інтерполяцією ряду динаміки. Приблизне визначення невідомих рівнів що лежать за межами одно якісного періоду, називають екстраполяцією ряду динаміки.

Інтерполяцію та екстраполяцію можна здійснювати різними способами. Найпростішим є використання середніх характеристик досліджуваного ряду динаміки: середнього абсолютного приросту і середнього коефіцієнта зростання(при стабільних темпах зростання). Однак визначення відсутніх рівнів ряду динаміки найчастіше пов’язують з аналітичним вирівнюванням рядів способом найменших квадратів, який дає найточніші результати.

Дослідження динаміки суспільних явищ і виявлення основної тенденції їхнього розвитку в минулому створюють основу для визначення їхніх майбутніх розмірів.

Екстраполяція відіграє важливу роль у плануванні. Вона дає змогу прогнозувати соціально-економічні явища. Прогнозування є важливим етапом планової роботи. [17, с. 234-242]

Застосування експоляції для прогнозування базується на припущенні, що характер динаміки, тобто певна тенденція зміни досліджуваного явища, яка мала місце для певного періоду часу в минулому, збережеться на обмеженому відрізку в майбутньому. Така експоляція справедлива, якщо система розкривається еволюційно в досить стабільних умовах. Чим крупніша система, тим більш ймовірно збереження параметрів її зміни, звісно на невеликий строк.

Користуючись цим методом слід пам’ятати, що можливості використання отриманих кривих для прогнозування надто обмежені, тому що зміна величини ознаки не є власне функцією часу. Крім того, закономірності і тенденції теперішнього часу не можна механічно переносити на майбутнє.

У зв’язку з цим прогнозуванню має передувати ретельний аналіз комплексу взаємопов’язаних факторів, які в майбутньому будуть визначати тенденцію розвитку досліджуваного соціально-економічного явища.

При вирівнюванні по середньому абсолютному приросту розрахункові рівні обчислюються за формулою:

,

де - вирівняні рівні;

- початковий рівень розподілу;

- середній абсолютний приріст;

Аналітичне вирівнювання способом найменших квадратів:

,

де , - невідомі параметри рівняння,

t – порядковий номер року.

Підставимо у наведені вище формули невідомі значення.

 

Таблиця 3.1

Прогнозування урожайності картоплі на 2009-2011 роки

Роки	Порядковий номер року	Урожайність, ц/га	Середній абсолютний приріст	Вирівнювання способом найменших квадратів
1998	0	72	72	83,14
1999	1	82	71,2	82,11
2000	2	95	70,4	81,08
2001	3	66	69,6	80,05
2002	4	75	68,8	79,03
2003	5	82	68	78
2004	6	98	67,2	76,97
2005	7	85	66,4	75,95
2006	8	77	65,6	74,92
2007	9	62	64,8	73,89
2008	10	64	64	72,86
Прогноз
2009	11	-	63,2	72,86
2010	12	-	62,4	70,81
2011	13	-	61,6	69,78

Графічне зображення прогнозу:

Рис.3.1 – Фактичні та прогнозовані рівні динаміки урожайності картоплі за середнім абсолютним приростом та прямою

Виконавши прогнозування методами вирівнювання за середнім абсолютним приростом та аналітичним вирівнюванням способом найменших квадратів, можна сказати що на 2009-2011 роки урожайність картоплі має тенденцію до зростання.

ВИСНОВКИ ТА ПРОПОЗИЦІЇ

На основі проведених в курсовому проекті розрахунків можна зробити такі висновки:

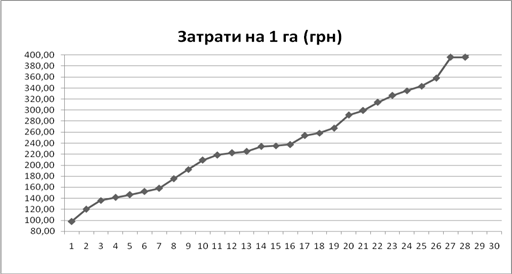
В цілому на врожайність картоплі найбільше впливає рівень затрат на 1 га площі картоплі. Слід також відмітити, що внесення мінеральних добрив на 1 га також визначає в певній мірі урожайність картоплі, судячи з результатів зведеного факторного групування. З таблиці 2.1.10 можна зробити висновок, що зі збільшенням внесених мінеральних добрив на 1 га посівів урожайність реагує по різному спочатку вона зростає, а потім зменшується, це пояснюється тим, що кількість внесення добрив має бути науково обґрунтованою і перевищення норми внесення може негативно вплинути на урожайність.

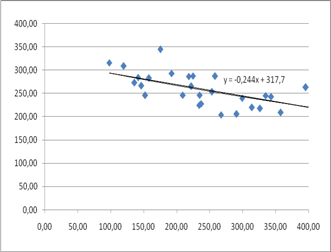
Кореляційний аналіз показує, що вимальовується майже прямолінійна залежність між затратами праці на 1га і урожайністю.

Розрахунковий коефіцієнт кореляції свідчить про те, що між показниками врожайності та розміром затрат на 1 га існує в даному випадку середній зв'язок.

Чим ближче значення до 1 тим зв'язок між ознаками тісніший.

Коефецієнт детермінації показує що на 22,3% результативна ознака y змінюється і залежить від впливу факторної ознаки x.

Аналіз рядів динаміки має за мету вивчення зміни явища за часом і встановлення його напрямку, характеру цієї зміни і вияв закономірності розвитку. Для оцінювання властивостей динаміки у даній роботі використовувались взаємопов’язані показники, або аналітичні показники.

У процесі аналізу динаміки урожайності картоплі я використовував абсолютний приріст, темпи зростання, приросту, абсолютне значення 1% приросту на основі порівняння рівнів ряду динаміки. За базу порівняння брав попередній, або початковий рівень динаміки.

В цілому дослідження показало що динаміка урожайності картоплі має тенденцію до зростання.

Індексний аналіз також показав тенденцію до зростання урожайності картоплі та посівної площі.

Виконавши прогнозування методами вирівнювання за середнім абсолютним приростом та аналітичним вирівнюванням способом найменших квадратів, можна сказати що на 2009-2011 роки урожайність картоплі має тенденцію до зростання.

Проаналізувавши всі вище названі розрахунки можна відмітити слідуючи пропозиції:

Найважливішим у комплексі заходів підвищення ефективності є використання земельних угідь на основі підвищення її родючості і зростання врожайності сільськогосподарських культур.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

1.  Головач А- В., Єріна А. М., Козырев О. В. Статистика- - К.: Вища школа, 1993.

2.  Гаркавий В. К. Статистика. —К.: Вища школа, 1995. – 412 с.

3.  Бутуцький О. А. Сільськогосподарська статистика з основами економічної статистики – К.: Вища школа, 1984.

4.  Статистика. Методичні вказівки по виконанню курсового проекту для студентів обліково-фінансового факультету денної та заочної форми навчання. – Вінниця, ВДАУ, 2010 – 36 с.

5.  Бухгалтерський звіт сільськогосподарського підприємства за 2006-2007 рр.

6.  Бек В.Л. Теорія статистики: Курс лекцій. Навч. посіб. для студ. вуз./ В.Л. Бек. – Київ: ЦУЛ, 2003. – 288 с.

7.  Беткита К.Ф. Економічна статистика: Курс лекцій: Навчальний посібник/ К.Ф. Беркита. – Київ: Професіонал, 2004. – 208 с.

8.  Вашків П.Г. Статистика підприємництва: Навч. посібник/ П.Г. Вашків, П.І. Пастер, В.П. Сторожук, Є.І. Ткач; за ред. П.Г. Вашківа, В.П. Сторожука. – К.: “Слобожащина”, 1999. – 600 с.

9.  Гаркавий В. К. Статистика. - К: Вища школа, 1995.- 412 с.

10.  Гончарук А.Г. Основи статистики: Навчальний посібник/ А.Г. Гончарук; Одеський національний політехнічний університет. – Київ: ЦУЛ, 2004. – 125 с.

11.  Статистика. Методичні вказівки по виконанню курсового проекту для студентів обліково-фінансового факультету денної та заочної форми навчання. – Вінниця, ВДАУ, 2002 – 36 с.

12.  Статистика: Підручник / С. С. Герасименко, А. В. Головач, А. М. Єріна та ін.; За наук. Ред. д-ра екон. наук С.С. Герасименка. – 2-ге вид., перероб. і доп. – К.: КНЕУ, 2000. – 467 с.

13.  Теорія статистики: Навчальний посібник / Вашків П. Г., Пастер П.І., Сторожук В.П., Ткач Є.І. – К.: Либідь, 2001. – 320 с.

14.  Чекотовський Е. В. Основи статистики сільського господарства: Навчальний посібник. – К.: КНЕУ, 2001. – 432 с.

15.  Штангрет А.М. Статистика: Навчальний посібник для студентів вищих навчальних закладів/ А.М. Штангрет, О.І. Копилюк; Міністерство освіти і науки України. – Київ: ЦУЛ, 2005. – 232 с.

ДОДАТОК 1

Статистичний аналіз урожайності картоплі

Шифр підприємства	Затрати – всього, тис. грн..	Прямі витрати праці, тис. люд.-год.	Оплата праці, тис. грн..	Внесено мінеральних добрив, кг д. р.	Валовий збір, тис. ц	Площа, га
1.	370,5	99,0	89,9	1636,5	176,6	1302,0
2.	245,3	108,0	73,6	1773,8	160,1	1161,0
3.	235,5	70,5	72,4	2065,5	173,3	1280,6
4.	266,3	78,0	76,4	760,5	156,8	1133,0
5.	211,5	89,3	69,3	1833,0	176,6	1295,5
6.	198,0	85,5	67,5	1458,8	163,4	1205,8
7.	228,0	87,8	71,4	2328,0	186,5	1374,2
8.	316,5	72,8	82,9	734,3	156,8	1139,5
9.	169,5	93,8	63,8	3939,0	236,0	1913,0
10.	207,8	67,5	68,8	1620,8	189,8	1399,5
11.	206,3	105,8	68,6	1495,5	156,8	1147,3
12.	170,3	71,3	63,9	2836,5	186,5	1385,9
13.	210,8	81,0	69,2	1448,3	170,0	1250,0
14.	253,5	72,0	74,7	1705,5	166,7	1216,2
15.	222,0	70,5	70,6	753,0	156,8	1142,8
16.	141,0	69,8	60,1	1698,0	170,0	1252,0
17.	194,3	65,3	67,0	2011,5	203,0	1419,0
18.	205,5	66,8	68,5	1890,0	209,6	1750,5
19.	153,0	100,5	61,7	2613,8	186,5	1381,3
20.	306,8	102,0	81,6	1948,5	170,0	1261,1
21.	198,0	75,0	67,5	1608,8	163,4	1196,1
22.	260,3	73,5	75,6	1483,5	184,8	1350,1
23.	189,0	72,0	66,3	2393,3	170,0	1250,7
24.	147,0	77,3	60,9	1464,0	178,2	1317,0
25.	200,3	71,3	67,8	1785,8	231,0	1880,5
26.	233,3	72,0	72,1	3810,8	186,5	1370,9
27.	246,0	87,8	73,7	2685,8	158,4	1138,2
28.	297,0	72,8	80,4	1723,5	170,0	1253,9
29.	338,3	93,8	85,7	1480,5	161,7	1188,3
30.	267,0	67,5	76,5	1240,5	171,6	1266,9

ДОДАТОК 2

Вихідні дані для обчислення динаміки

Шифри	Роки	Урожайність картоплі, ц/га
1	1998	72
2	1999	82
3	2000	95
4	2001	66
5	2002	75
6	2003	82
7	2004	98
8	2005	85
9	2006	77
10	2007	62
11	2008	64

 

ДОДАТОК 3

Статистичний аналіз урожайності картоплі

Підприємство	Площа, га		Урожайність, ц/га
	базисний період	звітний період	базисний період	звітний період
1.	105	120	106	106
2.	119	123	108	109
3.	125	122	121	117

ДОДАТОК 4

Вихідні та розрахункові дані для статистичного аналізу урожайності картоплі

Шифр підприємства	Затрати – всього, тис. грн..	Прямі витрати праці, тис. люд.-год.	Оплата праці, тис. грн..	Внесено мінеральних добрив, кг д. р.	Валовий збір, ц	Площа, га	Урожайність	Оплата праці 1 люд.-год., грн	Внесено добрив на 1 га	Прямі затрат праці на 1 га	затрати праці на 1 га грн
1.	205.5	99	89,9	1636,5	176600	1302	135,64	0,91	43,19	76	157,83
2.	200.3	108	73,6	1773,8	160100	1161	137,9	0,68	48,43	93	172,52
3.	169.5	70,5	72,4	2065,5	173300	1280,6	135,33	1,03	43,91	55	132,36
4.	170.3	78	76,4	760,5	156800	1133	138,39	0,98	49,63	68.8	150,31
5.	306.8	89,3	69,3	1833	176600	1295,5	136,32	0,78	43,4	68.9	236,82
6.	153	85,5	67,5	1458,8	163400	1205,8	135,51	0,79	46,63	71	126,89
7.	147	87,8	71,4	2328	186500	1374,2	135,72	0,81	40,92	64	106,97
8.	235.5	72,8	82,9	734,3	156800	1139,5	137,6	1,14	49,34	64.8	206,67
9.	267	93,8	63,8	3939	236000	1913	123,37	0,68	29,39	49.2	139,57
10.	198	67,5	68,8	1620,8	189800	1399,5	135,62	1,02	40,18	48	141,48
11.	297	105,8	68,6	1495,5	156800	1147,3	136,67	0,65	49,01	92.5	258,87
12.	207.8	71,3	63,9	2836,5	186500	1385,9	134,57	0,9	40,57	51	149,94
13.	370.5	81	69,2	1448,3	170000	1250	136	0,85	44,98	65	296,4
14.	228	72	74,7	1705,5	166700	1216,2	137,07	1,04	46,23	59	187,47
15.	141	70,5	70,6	753	156800	1142,8	137,21	1	49,2	62	123,38
16.	189	69,8	60,1	1698	170000	1252	135,78	0,86	44,91	56	150,96
17.	210.8	65,3	67	2011,5	203000	1419	143,06	1,03	39,63	46	148,56
18.	233.3	66,8	68,5	1890	209600	1750,5	119,74	1,03	32,12	38	133,28
19.	338.3	100,5	61,7	2613,8	186500	1381,3	135,02	0,61	40,71	73.5	244,91
20.	211.5	102	81,6	1948,5	170000	1261,1	134,8	0,8	44,59	81.3	167,71
21.	198	75	67,5	1608,8	163400	1196,1	136,61	0,9	47,01	63.1	165,54
22.	206.3	73,5	75,6	1483,5	184800	1350,1	136,88	1,03	41,65	54.2	152,8
23.	260.3	72	66,3	2393,3	170000	1250,7	135,92	0,92	44,96	58	208,12
24.	253.5	77,3	60,9	1464	178200	1317	135,31	0,79	42,69	59.3	192,48
25.	222	71,3	67,8	1785,8	231000	1880,5	122,84	0,95	29,9	38.7	118,05
26.	316.5	72	72,1	3810,8	186500	1370,9	136,04	1	41,02	53.4	230,87
27.	245.3	87,8	73,7	2685,8	158400	1138,2	139,17	0,84	49,4	77.3	215,52
28.	266.3	72,8	80,4	1723,5	170000	1253,9	135,58	1,1	44,84	58.2	212,38
29.	246	93,8	85,7	1480,5	161700	1188,3	136,08	0,91	47,32	79	207,02
30.	194.3	67,5	76,5	1240,5	171600	1266,9	135,449	1,133	44,382	53	153,37