Навигация
1.2.2 Метод Неймана
Для получения псевдослучайной последовательности Фон Нейманом был придуман простой в вычислительном отношении алгоритм, известный как метод квадратов. Метод состоит в многократном повторении процедуры, состоящей в возведении в квадрат некоторого числового значения и взятия средних цифр полученного результата. Пусть, например, мы выбрали в качестве исходного значения число 
. Тогда 
и 
, 
и 
, и так далее. Однако вскоре у метода обнаружился недостаток, заключающийся в существенной неравномерности статистических частот различных числовых значений элементов получаемой этим методом последовательности.
1.2.3 Мультипликативный конгруэнтный метод
Этот метод основан на рекуррентном вычислении элементов псевдослучайной последовательности как результата выполнения операции сравнения по некоторому заданному основанию. Переход к следующему числу последовательности производится простым умножением результата сравнения на некоторую заданную константу. На практике операции вычисления произведения и взятия сравнения по заданному основанию совмещены. В качестве основания сравнения используется величина 
, где m – разрядность целочисленного регистра ЭВМ, в котором хранится результат вычисления произведения.
При целочисленном умножении этого результата на заданную константу достаточно большой величины происходит переполнение, вследствие чего в регистре результата сохраняются лишь m младших разрядов произведения. Это число фактически и будет результатом операции сравнения вычисленного произведения с числом , (напомним, что операцией сравнения по некоторому основанию называется вычисление остатка от деления первого операнда на это основание).
Формально схема вычисления может быть определена следующим образом: 
= С, 
(mod
), где 
i-ый член псевдослучайной последовательности, С – некоторая константа, m – разрядность целочисленного регистра ЭВМ. Качество полученной псевдослучайной последовательности зависит от выбранного значения константы С. Установлено, что хороший результат достигается при выборе ее значения равным максимальной нечетной степени числа 5, помещающегося в числовом регистре фиксированной разрядности. Для 32-х разрядного регистра ЭВМ это число будет 
.
1.2.4 Равномерное распределение
Случайная величина ξ, с равномерным распределением на отрезке [а,b] описывается функцией плотности вероятности:
P(x)=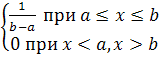
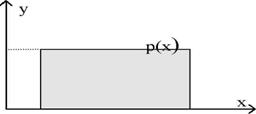
a b
Рис.2 Равномерное распределение
Математическое ожидание
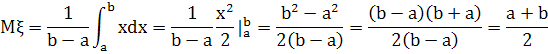
Для вычисления дисперсии вначале вычислим математическое ожидание квадрата этой случайной величины:
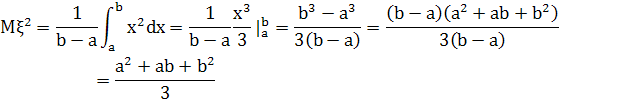
Теперь:
=
1.2.5 Моделирование дискретной случайной величины
Предположим вначале, что нам требуется смоделировать простейшую дискретную случайную величину, принимающую два значения с равными вероятностями. Эта случайная величина моделирует выбрасывание жребия или монеты. Если мы имеем в своем распоряжении генератор псевдослучайных последовательностей, описанный в предыдущем параграфе, то задача может быть решена следующим, достаточно очевидным, способом. Поскольку псевдослучайное число, получаемое с помощью функции rand(), распределено равномерно в интервале (0,1), то одинаково вероятно, будет ли очередное полученное значение принадлежать левой половине этого интервала [0,0.5) или правой [0.5, 1]. По этой причине мы можем одно из двух значений нашей случайная величина поставить в соответствие первому из этих двух подинтервалов, а в другое – второму, и далее выдавать значения в зависимости от того к какому из этих двух подинтервалов будет принадлежать очередное выпавшее значение генератора rand(). Эта схема, очевидно, легко обобщается на дискретную случайная величина, принимающую более двух значений. За каждым значением мы должны в этом случае «закрепить» некоторый подинтервал значений функции rand() с длиной, равной вероятности этого значения моделируемой дискретной случайная величина, - причем так, чтобы интервалы , закрепленные за различными значениями случайные величины не пересекались бы между собой. Поскольку сумма вероятностей всех значений случайная величина равна 1, и таков же диапазон значений, принимаемых псевдослучайной величиной, генерируемой функцией rand(), то эти подинтервалы полностью покроют диапазон возможных значений, принимаемых случайная величина, генерируемой функцией rand().
Теперь мы должны лишь всякий раз определять, к какому из множеству выбранных указанным выше образом подинтервалов принадлежит очередное выданное функцией rand() значение, и выдавать соответствующее ему значение моделируемой дискретной случайная величина.
Формально этот метод может быть представлен в следующем виде. Пусть 
– случайная величина, равномерно распределенная на отрезке [0,1] (в нашем случае – это результат очередного выполнения функции rand()) и 
– моделируемая дискретная случайная величина с распределением 
. Тогда мы выдаем по получении очередного значения g случайной величины такое значение 
дискретной случайной величины , для которого верно двойное неравенство 
. Этим исчерпывается решение задачи моделирования дискретной случайной величины с заданным распределением. Вышеприведенный алгоритм легко реализуется программно, - например так, как в нижеприведенной функции int discrete (float p[]):
unsigned int discrete (float p[])
{
float s, r;
int k=0;
s=p[0]; r=rand();
while (s < r)
{
k++;
s=s+p[k];
}
return k;
}
Функция принимает массив вероятностей моделируемой дискретной случайной величины и выдает индекс очередного ее сгенерированного значения. Следует учесть, что поскольку индексация массивов в языке С начинается с нуля, также с нуля индексируются значения разыгрываемой случайной величины. То есть функция выдает значения в диапазоне от 0 до к-1 для дискретной случайной величины, принимающей к значений. Ниже для иллюстрации приведен ряд из 100 значений выданных программой, использующей вызов данной функции для массива вероятностей p={0.5, 0.5}:
0 1 1 1 0 0 0 1 1 1 1 1 1 0 1 0 0 1 1 0 1 1 0 0 0 0 0 1 0 1 0 0 0
1 0 1 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0
1 0 1 0 1 1 1 0 0 1 1 0 1 0 1 0 0 1 1 1 1 0 0 0 0 1 0 1 0 0 0 0 1
1.2.6 Моделирование случайной величины, равномерно распределенной в интервале (a,b)
Мы используем метод обратной функции для моделирования равномерного и показательного распределений. Решаем уравнение 
. Для этого, подставив выражение для плотности равномерного распределения на место 
, вначале вычислим интеграл в левой части уравнения:
,
а затем для вычисления значений u равномерно распределенной в интервале (a,b) случайной величины через значения g случайной величины 
, равномерно распределенной в интервале (0,1) просто выразим переменную u через переменную g из уравнения 
:
Заметим, что полученная формула очевидна. Действительно, для пересчета равномерно распределенной в интервале (0,1) случайной величины в случайную величину, равномерно распределенную в интервале (a,b), мы должны вначале «растянуть» диапазон значений единичной длины в диапазон значений (b-a) умножая значения g на (b-a), а затем переместить полученный результат из интервала (0,1) в интервал (a,b), прибавив к нему значение a.
Запись полученной формулы в виде функции языка С:
float uniform (float a, float b) {return rand()*(b-a)+a;}
позволит нам программно генерировать случайные величины с равномерным распределением в любом заданном конечном интервале значений (a,b).
Глава 2 Имитационное моделирование процесса
Похожие работы
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... ai- расход сырья на единицу продукции; B - общий запас сырья; W - область допустимых ограничений; Тема 2. Метод математического моделирования в экономике. 2.1. Понятие “модель” и “моделирование”. С понятием “моделирование экономических систем” (а также математических и др.) связаны два класса задач: 1) задачи анализа, когда система подвергается глубокому изучению ее ...
... Математическое моделирование — метод изучения объекта исследования, основанный на создании его математической модели и использовании её для получения новых знаний, совершенствования объекта исследования или управления объектом. Математическое моделирование можно подразделить на аналитическое и компьютерное (машинное) моделирование. При аналитическом моделировании ученый — теоретик получает ...
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
0 комментариев