Навигация
Умовне середнє і вибіркова регресія
2.3 Умовне середнє і вибіркова регресія
У математичній статистиці вводять вибіркові оцінки умовного математичного сподівання і регресії. У якості оцінки умовного математичного сподівання ![]() беруть умовне середнє
беруть умовне середнє ![]() , яке знаходять за вибірковими даними спостережень.
, яке знаходять за вибірковими даними спостережень.
Умовним середнім ![]() називається середнє арифметичне значень випадкової величини
називається середнє арифметичне значень випадкової величини ![]() , що спостерігаються за умови, яка випадкова величина
, що спостерігаються за умови, яка випадкова величина ![]() при цьому має значення
при цьому має значення ![]() . Аналогічно визначається і умовне середнє
. Аналогічно визначається і умовне середнє ![]() , однак надалі для стислості викладення обмежимося в основному розглядом тільки
, однак надалі для стислості викладення обмежимося в основному розглядом тільки ![]() і пов'язаними з ним питаннями.
і пов'язаними з ним питаннями.
Також як і умовне математичне сподівання ![]() , його вибіркова оцінка є функцією від змінної
, його вибіркова оцінка є функцією від змінної ![]() , що позначимо через
, що позначимо через ![]() і будемо називати вибірковою регресією
і будемо називати вибірковою регресією ![]() на
на ![]() , а її графік – вибірковою лінією регресії
, а її графік – вибірковою лінією регресії ![]() на
на ![]() . Крім того, за аналогією з рівняннями (8) і (9) вводяться вибіркові рівняння регресії
. Крім того, за аналогією з рівняннями (8) і (9) вводяться вибіркові рівняння регресії ![]() на
на ![]() і
і ![]() на
на ![]() , відповідно
, відповідно
![]() (14)
(14)
![]() (15)
(15)
2.4 Визначення параметрів вибіркового рівняння прямої лінії середньоквадратичної регресії за незгрупованих даних
Нехай під час дослідження кількісних ознак (![]() ,
, ![]() ) у результаті
) у результаті ![]() незалежних випробувань отримано
незалежних випробувань отримано ![]() пар чисел:
пар чисел: ![]() ,
,![]() ,...,
,...,![]() . Будемо шукати функцію
. Будемо шукати функцію ![]() в лінійному наближенні (все аналогічно проводиться і для функції
в лінійному наближенні (все аналогічно проводиться і для функції ![]() у випадку регресії
у випадку регресії ![]() на
на ![]() ). Крім того, у припущенні незгрупованих даних спостережень (різні значення
). Крім того, у припущенні незгрупованих даних спостережень (різні значення ![]() ознаки
ознаки ![]() і відповідні їм значення
і відповідні їм значення ![]() ознаки
ознаки ![]() спостерігалися по одному разу)
спостерігалися по одному разу) ![]() і
і ![]() можна замінити на
можна замінити на ![]() і
і ![]() . Під час цього рівняння прямої лінії регресії
. Під час цього рівняння прямої лінії регресії ![]() на
на ![]() можна подати у вигляді
можна подати у вигляді
![]() (16)
(16)
Кутовий коефіцієнт ![]() прямої (16) називається вибірковим коефіцієнтом регресії
прямої (16) називається вибірковим коефіцієнтом регресії ![]() на
на ![]() і позначається
і позначається ![]() . Він є оцінкою коефіцієнта регресії
. Він є оцінкою коефіцієнта регресії ![]() в рівнянні (10). Тепер рівняння (16) можна переписати
в рівнянні (10). Тепер рівняння (16) можна переписати
![]() (17)
(17)
Підберемо параметри ![]() і
і ![]() так, щоб сума квадратів відхилень прямої (17) від точок
так, щоб сума квадратів відхилень прямої (17) від точок ![]() ,
,![]() ,...,
,...,![]() , побудованих за даними спостережень, була б мінімальною
, побудованих за даними спостережень, була б мінімальною
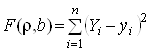 (18)
(18)
де
![]() – ордината, що спостерігається, і є відповідною до
– ордината, що спостерігається, і є відповідною до ![]() ,
,
![]() – ордината точки, що лежить на прямій (17) і має абсцису
– ордината точки, що лежить на прямій (17) і має абсцису ![]() ,
,
![]() .
.
Підставивши значення ![]() з рівняння (17) у формулу (18), одержимо
з рівняння (17) у формулу (18), одержимо
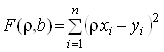 (19)
(19)
Дорівнявши нулю частинні похідні ![]() і
і ![]() функції (19) одержимо систему двох лінійних алгебраїчних рівнянь щодо параметрів
функції (19) одержимо систему двох лінійних алгебраїчних рівнянь щодо параметрів ![]() і
і ![]() для знаходження точки її мінімуму
для знаходження точки її мінімуму
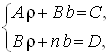 (20)
(20)
де
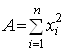 ,
,  ,
, 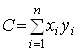 ,
, 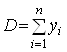
звідкіля остаточно знаходимо

Аналогічно визначається вибіркове рівняння прямої лінії регресії ![]() на
на ![]() .
.
Похожие работы
... іжності між емпіричними і теоретичними частотами розподілу не можуть бути випадковими і припущення про близькість емпіричного розподілу до нормального повинна бути спростоване. Розділ 3. Кореляційний аналіз виробництва льоноволокна Одним з найважливіших завдань статистики є вивчення об'єктивно існуючих зв'язків між явищами. При дослідженні таких зв'язків з'ясовуються причинно-наслідкові ві ...
... із виконання доходної та видаткової частини бюджету. Отже, наступний розділ дипломної роботи присвятимо висвітленню характеристики і поглибленому аналізу стану даної проблеми. Розділ 2. Аналіз виконання і планування місцевих бюджетів 2.1 Аналіз виконаня місцевих бюджетів по Харківській області Місцевий бюджет виконується за розписом, який затверджується керівником місцевого фінансового ...
... ійний аналіз. Широко застосовуються метод експертних оцінок і рангової кореляції, способи парної і множинної кореляції. Велику роль у фінансовому аналізі відіграє експертний метод (інша назва — прийом експертних оцінок). Сутність його полягає у збиранні думок спеціалістів щодо поставленої проблеми, подальше опрацювання їх і використання в аналітичній роботі. Для оцінювання думок експертів про ...
... місцях по обсягам валюти балансу та обсягів балансового прибутку, за рівнем рентабельності активів та статутного капіталу ЗАТ КБ «Приватбанк» суттєво програє банкам, які спеціалізуються на роботі з юридичними особами. ВИСНОВКИ Досліджена в дипломному проекті фінансова діяльність комерційного банку – це діяльність, яка спричиняє зміни розміру та складу власного і залученого/запозиченого капіталу ...







0 комментариев