Точечные оценки для средней и дисперсии генеральной совокупности

3.4 Точечные оценки для средней и дисперсии генеральной совокупности

Обозначим через  и σ² среднюю и дисперсию генеральной совокупности.

Возвратная выборка объема n может рассматриваться как совокупность n независимых случайных величин X_j, имеющих одно и то же распределение, совпадающее с генеральным, для которых, следовательно:

M(X_j) = ; D(X_j) = σ²

Для точечной оценки генеральной средней естественно использовать статистику  ¾ среднюю. Используя свойства математического ожидания и дисперсии, получим:

(1.9.16)

(1.9.17)

Нетрудно видеть, что статистика θ ¾ X* является состоятельной, несмещенной и эффективной оценкой параметра  .

Для точечной оценки генеральной дисперсии воспользуемся статистикой  — выборочной дисперсией. Однако при ближайшем рассмотрении оказывается, что

(1.9.18)

Таким образом, статистика θ = D* является смещенной оценкой для генеральной дисперсии σ². Однако смещенность легко устраняется путем введения корректирующего множителя . Статистика

(1.9.19)

(так называемая «исправленная» выборочная дисперсия) является несмещенной оценкой генеральной дисперсии σ² и используется для ее точечной оценки.

Заметим, что при большом п отношение  и потому значение s²≈D*

В случае безвозвратной выборки можно показать, что точечная оценка средней будет той же (т. е. *), а точечная оценка дисперсии должна быть заменена на:

(1.9.20)

где N — объем генеральной совокупности

В случае безвозвратной выборки изменится и выражение для D(*), которое потребуется для построения доверительного интервала при оценке средней:

(1.9.21)

При относительно небольшом объеме выборки  и

3.5 Интервальные оценки средней

 

При изложении данного вопроса будем различать случаи больших и малых выборок. При этом оба случая сначала рассмотрим в более простой, с теоретической точки зрения, ситуации возвратной (повторной) выборки.

3.5.1 Большая выборка

Если объем выборки достаточно большой (практически, начиная с п > 20—30), то распределение выборочной средней , согласно центральной предельной теореме, независимо от характера генерального распределения приближается к нормальному распределению с параметрами

 

М()= и )

где  — генеральная средняя,

σ— генеральное среднее квадратическое отклонение,

п — объем выборки.

Таким образом, величина

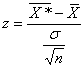
распределена по стандартному нормальному закону (с математическим ожиданием M(z) = 0 и средним квадратическим отклонением σ(z) = 1).

Задавшись доверительной вероятностью Р = 1 — α, определяем из равенства 2Ф(z) = 1 — α соответствующее значение z_a (используем при этом таблицу интегральной функции Лапласа). Тогда с вероятностью Р = 1 — α выполняется неравенство:

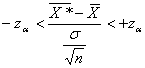(1.9.22)

которое эквивалентно неравенству:

(1.9.23)

Величина называется предельной ошибкой выборки.

Таким образом, мы имеем доверительный интервал для генеральной средней:

( ; )

Наоборот, если задана предельная ошибка ε , а требуется определить вероятность Р, то схема решения задачи следующая:

ε→z=→Ф(z)→P=2Ф(z) (1.9.24)

Наконец, определение объема выборки п по данным Р и ε производится по следующей схеме:

 

P=2Ф(z) →z→n= (1.9.25)

 

Пример 1.9.4. Взвешивание 50 случайно отобранных коробок печенья дало =1200г. Определить с вероятностью Р = 0,95 доверительные границы для среднего веса коробки печенья  в генеральной совокупности, если есть основания полагать, что генеральная дисперсия σ² = 11664.

Решение:

Дано: n=50; =1200; σ² =11664 (= 108); Р = 0,95.

Из равенства Р = 2Ф(z)=0,95 по таблице значений интегральной функции Лапласа находим z=1,96, откуда:

ε=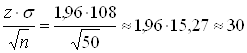(г)

Таким образом, получаем доверительный интервал:

1200 — 30 < < 1200 + 30.

 

Пример 1.9.5 Определить, с какой доверительной вероятностью можно утверждать, что при данном объеме выборки (50 коробок) ошибка выборки не превысит 20 г.

Решение:

По величине ε=20 вычисляем , откуда по таблице Ф(z): Р = 2Ф(1,31)≈0,81

Пример 1.9.6. Определить необходимый объем выборки n, который с вероятностью 0,99 гарантировал бы ошибку выборки не более чем ε = 20 г.

Решение:

Из Р = 2Ф(z) =0,99 находим z = 2,58, откуда:

 коробок

Предположение о том, что генеральная дисперсия σ² известна при неизвестной генеральной средней, на практике выполняется весьма редко. Чаще всего мы имеем лишь выборочные данные и можем дать лишь выборочную оценку s² неизвестной дисперсии σ².

Статистика

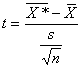(1.9.26)

подчиняется закону распределения Стьюдента с v = n—1 степенями свободы. Однако при больших значениях параметра v (v ≥ 30) распределение Стьюдента практически совпадает с нормальным. Поэтому в случае больших выборок схема решения задач остается прежней, даже если вместо 'Неизве стного генерального среднего квадратического отклонения а используется его выборочная оценка s.