Собственно случайная выборка
Строим ранжированный ряд данных по уровню рентабельности продукции и сортируем по возрастанию
Строим аналитическую таблицу
Строим график полученного ряда распределения, на котором графически определяем моду и медиану. Для построения графика используем таблицу 7
Находим ошибку выборки доли организаций с уровнем рентабельности продукции 23,9% и более и границы, в которых будет находиться генеральная доля
Находим средний стаж работников. Для этого необходимо построить таблицу, в которой находим середину интервала
Навигация
Выборочный метод изучения производственных и финансовых показателей
Выборочный метод изучения производственных и финансовых показателей
35156
знаков
13
таблиц
5
изображений
Федеральное агентство по образованию
Всероссийский заочный финансово – экономический институт
Кафедра статистики
КУРСОВАЯ РАБОТА
по дисциплине "Статистика"
на тему
"Выборочный метод изучения производственных и финансовых показателей"
Оглавление
Введение
Теоретическая часть
Расчетная часть
Аналитическая часть
Заключение
Список используемой литературы
Введение
Цель работы – составить общее представление о выборочном методе и о возможностях его применения в экономике. Работа содержит классификацию типов случайной и неслучайной выборки, описание каждого метода, их преимущества и недостатки. Для каждого типа случайной выборки приведены формулы расчета ошибки репрезентативности (выборочного среднего) и объема выборки.
Суть выборочного метода и его роль в экономике.
Одной из задач, которые стоят перед экономистом при проведении исследования, является сбор необходимых данных об объекте исследования. Множество элементов, составляющих объект исследования, называют генеральной совокупностью (ГС). Наиболее простым, на первый взгляд, способом сбора данных является сплошное обследование ГС. Однако применение сплошного обследования не всегда представляется возможным. В этом случае применяется выборочное обследование. Суть выборочного метода заключена в том, что обследованию подвергается только часть элементов ГС, которая называется выборочной совокупностью (ВС).
Выборочный метод имеет более широкую область применения. Широта области применения выборочного метода объясняется тем, что небольшой (по сравнению с ГС) объем выборки позволяет использовать более сложные методы обследования, включая использование различных технических средств (например, видео- и аудиоаппаратуры).
Следует различать единицы отбора и единицы наблюдения. Единицами отбора являются единицы или группы единиц ГС, отбираемые на каждом этапе формирования ВС. Единицы наблюдения – это отобранные единицы ГС, характеристики которых непосредственно измеряются. Если выборка проходит в несколько этапов (многоступенчатая выборка), то единицы отбора и единицы наблюдения могут не совпадать.
Разделяют два типа ошибок. Случайная (статистическая) ошибка – это ошибки, которые возникают вследствие случайной вариации значений, вызванной тем, что наблюдается только часть единиц, а не вся ГС. Случайные ошибки уменьшаются с увеличением объема ВС. Случайную ошибку можно измерить методами математической статистики, если при формировании ВС соблюдался принцип случайности. Принцип случайности заключается в следующем: каждый элемент ГС имеет равную и отличную от нуля вероятность попасть в ВС.
Теоретическая часть
Общая характеристика выборочного методаТеоретической основой выборочного метода является закон больших чисел. В силу этого закона при ограниченном рассеивании признака в генеральной совокупности и достаточно большой выборке с вероятностью, близкой к полной достоверности, выборочная средняя может быть сколь угодно близка к генеральной средней. Закон этот, включающий в себя группу теорем, доказан строго математически. Таким образом, средняя арифметическая, рассчитанная по выборке, может с достаточным основанием рассматриваться как показатель, характеризующий генеральную совокупность в целом.
Разумеется, не всякая выборка может быть основой для характеристики всей совокупности, к которой она принадлежит. Таким свойством обладают лишь репрезентативные (представительные) выборки, т. е. выборки, которые правильно отражают свойства генеральной совокупности. Существуют способы, позволяющие гарантировать достаточную репрезентативность выборки. Как доказано в ряде теорем математической статистики, таким способом при условии достаточно большой выборки является метод случайного отбора элементов генеральной совокупности, такого отбора, когда каждый элемент генеральной совокупности имеет равный с другими элементами шанс попасть в выборку. Выборки, полученные таким способом, называются случайными выборками. Случайность выборки является, таким образом, существенным условием применения выборочного метода.
Статистическое наблюдение можно организовать сплошное и несплошное. Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности и связано с большими трудовыми и материальными затратами. Изучение не всех единиц совокупности, а лишь некоторой части, по которой следует судить о свойствах всей совокупности в целом, можно осуществить несплошным наблюдением. В статистической практике самым распространенным является выборочное наблюдение.
Выборочное наблюдение - это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность.
Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели - генеральными.
Совокупность отобранных единиц именуют выборочной совокупностью, и все ее обобщающие показатели - выборочными.
При любых статистических исследованиях возникают ошибки двух видов: регистрации и репрезентативности.
Ошибки регистрации могут иметь случайный (непреднамеренный) и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного направления в сторону преувеличения или преуменьшения значения изучаемого показателя. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора (предвзятые цели). Их можно избежать при правильной организации и проведении наблюдения.
Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборных и соответствующих генеральных показателей.
По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности; при групповом отборе - качественно однородные группы или серии изучаемых единиц; комбинированный отбор предполагает сочетание первого и второго видов.
По методу отбора различают повторную и бесповторную выборки.
При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку ("отбор по схеме возвращенного шара"). Повторная выборка в социально-экономической жизни встречается редко. Обычно выборку организуют по схеме бесповторной выборки.
При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т.е. последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц ("отбор по схеме невозвращенного шара"). Таким образом, при бесповторной выборке численность единиц генеральной совокупности сокращается в процессе исследования.
Виды выборочного изучения
В зависимости от того, как осуществляется отбор элементов совокупности в выборку, различают несколько видов выборочного обследования. Отбор может быть случайным, механическим, типическим и серийным.
Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами:
N - объем генеральной совокупности (число входящих в нее единиц);
n - объем выборки (число обследованных единиц);
- генеральная средняя (среднее значение признака в генеральной совокупности);
- выборочная средняя;
р - генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности);
w - выборочная доля;
s2 - генеральная дисперсия (дисперсия признака в генеральной совокупности);
S2 - выборочная дисперсия того же признака;
s - среднее квадратическое отклонение в генеральной совокупности;
S - среднее квадратическое отклонение в выборке.
Похожие работы
... невозвращенного шара"). Таким образом, при бесповторной выборке численность единиц генеральной совокупности сокращается в процессе исследования. 1.2 Финансовые показатели Финансовые показатели - набор показателей, использующихся для исследования эффективности деятельности компании, и измерения степени риска ее операций. Обычно выделяют четыре группы показателей: коэффициенты рентабельности, ...
... если перенести начало отсчета в середину рассматриваемого периода. Прогнозирование и интерполяция Прогнозирование (экстраполяция) – это определение будущих размеров экономического явления. Интерполяция – это определение недостающих показателей уровней ряда. Наиболее простым методом прогнозирования является расчет средних характеристик роста (средний абсолютный прирост, средний темп роста и т.д.) ...
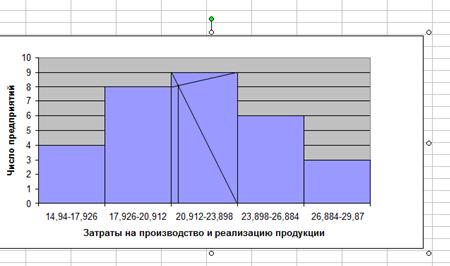
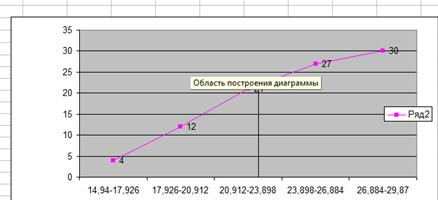
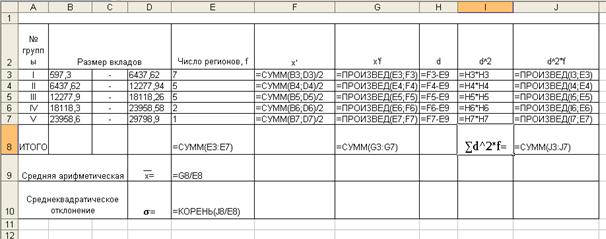
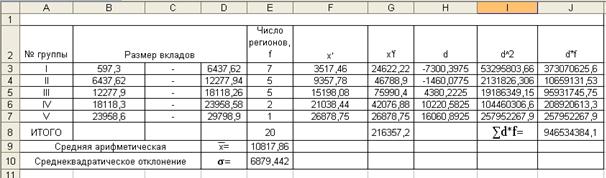
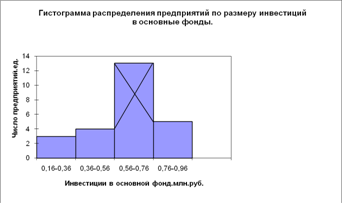
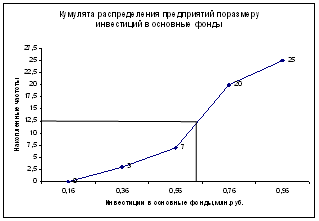
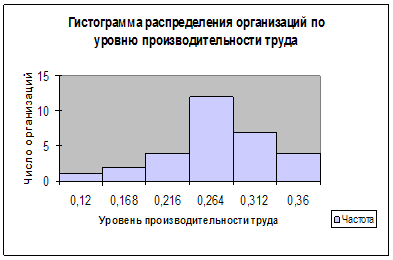
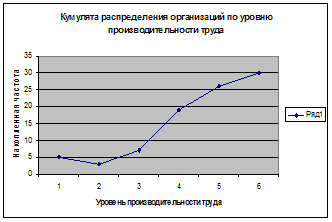
... тенденции свидетельствуют о благоприятном развитии экономики, расширении деятельности предприятий и организаций, увеличении предпринимательской активности.2. Расчетная часть Вариант №2 Тема. Статистические методы изучения инвестиций Имеются следующие выборочные данные по 25-ти однотипным предприятиям одного из регионов РФ, для анализа инвестирования предприятий собственными средствами за ...
... группы, установление связи и ее направление. Индексный метод является гибким аналитическим инструментом и может применяться в анализе показателе производственной, финансовой, инвестиционной и других видах деятельности предприятия (фирмы). Корреляционный и регрессионный анализ являются довольно сложной операцией. Исходными предпосылками для их проведения являются: случайный характер факторов, ...
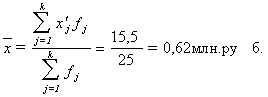
0 комментариев